Tartalom
- Előszó
- 1. Egyenes vonalú egyenletes mozgás vizsgálata Mikola-csővel
- 2. Egyenes vonalú egyenletesen gyorsuló mozgás vizsgálata
- 3. A dinamika alapegyenletének vizsgálata Atwood-féle ejtőgéppel
- 4. A nehézségi gyorsulás meghatározása matematikai ingával
- 5. Tehetetlenségi nyomaték meghatározása fizikai inga lengésidejének mérésével
- 6. Egyenletesen gyorsuló forgómozgás vizsgálata
- 7. Ideális gáz állapotegyenletének kísérleti igazolása
- 8. Légnyomás meghatározása Melde-csővel
- 9. Kaloriméter hőkapacitásának és szilárd test fajhőjének meghatározása
- 10. A jég olvadáshőjének meghatározása keverési kaloriméterrel
- 11. Mikroszkóp okulárskálájának hitelesítése, hosszúságmérés mikroszkóppal
- 12. Fókusztávolság meghatározása a leképezési törvény alapján
- 13. Optikai mérések Hartl-koronggal
- 14. Ohm-törvény vizsgálata
- 15. Ellenállások soros és párhuzamos kapcsolása
- 16. Vizsgadolgozatok
A táblázatok listája
- 1.1. Táblázat az 1. feladat mérési eredményeihez.
- 1.2. Táblázat a 3. feladat mérési eredményeihez.
- 2.1. Táblázat az 1., 2. és 3. feladat mérési eredményeihez.
- 3.1. Táblázat a 2., 3., 4. és 5. feladat mérési eredményeihez.
- 4.1. Táblázat az 1. és 2. feladat mérési eredményeihez.
- 5.1. Táblázat a 3. feladat mérési eredményeihez.
- 6.1. Táblázat az 1. feladat mérési eredményeihez.
- 6.2. Táblázat a 6. feladat mérési eredményeihez.
- 7.1. Táblázat az 1. feladat mérési eredményeihez.
- 8.1. Táblázat a mérési eredményeknek.
- 9.1. Táblázat az 1. feladat mérési eredményeihez.
- 9.2. Táblázat a 3. feladat mérési eredményeihez.
- 10.1. Táblázat az 1. és 2. feladat mérési eredményeihez.
- 12.1. Táblázat a 3. feladat mérési eredményeihez.
- 12.2. Táblázat a 4. feladat mérési eredményeihez.
- 13.1. Táblázat az 1. feladathoz.
- 13.2. Táblázat a 2. feladathoz.
- 13.3. Táblázat a 3. feladathoz.
- 13.4. Táblázat a 4. feladathoz.
- 14.1. Táblázat a mérési eredményekhez.
- 15.1. Táblázat az 1. és 3. feladat mérési eredményeihez.
- 15.2. Táblázat a 5. és 7. feladat mérési eredményeihez.
Társadalmi Megújulás Operatív Program
Tananyagfejlesztés és tartalomfejlesztés különös tekintettel a matematikai, természettudományi, műszaki és informatikai (MTMI) képzésekre
című pályázat
Kódszám: TÁMOP 4.1.2-08/1/A
A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósult meg.
A 2006/2007. tanév jelentős változásokat hozott a felsőoktatásban. A műszaki és természettudományos képzésekben általánosan bevezetésre került a háromlépcsős (BSc, MSc és PhD) képzés. A változások sok új, korábban még nem oktatott kurzus bevezetését is eredményezték.
A Szegedi Tudományegyetem Természettudományi és Informatikai Karán valamint a Juhász Gyula Pedagógusképző Karon folyó fizika alapképzés (BSc-képzés) egyik új, kötelező kurzusa az Alapozó laboratóriumi gyakorlatok c. tárgy. (Kurzusfelelős: Farkas Zsuzsanna, főiskolai tanár.) Természetesen ezen új tantárgyhoz a korábbiakban még nem állt, nem állhatott rendelkezésre a hallgatók felkészülését segítő, azt lehetővé tevő kiadvány. Ennek a hiánynak a pótlására készítettük el az "Alapozó laboratóriumi gyakorlatok" című tankönyvet. A szerzők: Dr. Farkas Zsuzsanna, Dr. Horváth Zoltán, Alapozó laboratóriumi gyakorlatok, Egyetemi tankönyv, JGYF Kiadó, 2007.
A kurzus tematikáját úgy állítottuk össze, hogy a gyakorlatokat végző hallgatókban a középiskolai fizika tanulmányokra és ismeretekre alapozva - kialakítsa azokat a készségeket, amelyek feltétlenül szükségesek a későbbi, felsőbb éves fizikai laboratóriumi gyakorlatok elvégzéséhez is.
A tankönyv a Nemzetközi Mértékegységrendszer alapegységeinek, kiegészítő egységeinek, valamint az önálló mértékegységgel rendelkező fizikai mennyiségeknek az áttekintésével kezdődik. Az olvasó a továbbiakban, a fizikában is jelentőséggel bíró prefixumokról szerezhet ismereteket. Ezután 16 laboratóriumi gyakorlat leírása következik, mintegy 60 oldalnyi terjedelemben. A gyakorlatok közül 7 a mechanika, 4 a hőtan, 3 az optika, 2 pedig az elektromosságtan témaköréből kerül ki. Tekintettel arra, hogy a heti két órás laboratóriumi gyakorlatokra fordítható hetek száma egy egyetemi szemeszterben legfeljebb 13 vagy 14, így a tankönyv "tartalék" gyakorlatokat is tartalmaz.
A tárgyat gondozó, a képzésért felelős Általános és Környezetfizikai Tanszék fizikai műszer- és eszközparkja biztosíték arra, hogy a gyakorlatokhoz szükséges fizikai- és egyéb mérőeszközök jó minőségben és kellő számban rendelkezésre álljanak.
A tankönyvben leírt gyakorlatok anyaga egy rövid elméleti összefoglalással kezdődik, ami még azok számára is lehetővé teszi az adott gyakorlat elvégzéséhez szükséges ismeretek megszerzését, akik egyébként ilyen ismeretekkel nem rendelkeznek kellő mértékben. Ezután a mérés menete, a mérőeszközök leírása következik. A gyakorlatok zöménél fizikatörténeti ismeretekhez is juthat az olvasó. Ennek során a hallgató megismerheti egy-egy eszköz, egy-egy törvény névadóját.
A hallgatók otthoni felkészülését a tankönyv azzal is segíti, hogy a gyakorlatokhoz elkészítettük a mérési adatok gyűjtéséhez szükséges táblázatokat, illetve azzal, hogy az alkalmazott kísérleti eszközökről készült fényképek és magyarázó ábrák is helyet kapnak a tankönyvben.
Az elvégzendő feladatokat pontosan, pontokba szedve adtuk meg. A hallgatók munkáját azzal is segítettük, hogy megadtuk a mérés során nyert mérési eredmények rögzítéséhez, kigyűjtéséhez szükséges táblázatokat. Ez nagymértékben megkönnyíti a hallgatók munkáját, sőt nagyfokú időnyereséggel is együtt jár. A gyakorlatok, valamint a tankönyv végén megtalálhatjuk a felhasznált és ajánlott szakmai irodalomjegyzéket is.
A tankönyv tematikája:
Mechanika
Egyenes vonalú egyenletes mozgás vizsgálata Mikola-csővel
Egyenes vonalú egyenletesen gyorsuló mozgás vizsgálata
A dinamika alapegyenletének vizsgálata Atwood-féle ejtőgéppel
A nehézségi gyorsulás meghatározása matematikai ingával
Tehetetlenségi nyomaték meghatározása fizikai inga lengésidejének mérésével
Egyenletesen gyorsuló forgómozgás dinamikai vizsgálata
Csatolt ingák vizsgálata vektorszkóp (V-scope) rendszerrel
Hőtan:
Ideális gáz állapotegyenletének kísérleti igazolása
Mérések Melde-csővel
Kaloriméter hőkapacitásának és szilárd test fajhőjének meghatározása
Jég olvadáshőjének meghatározása keverési kaloriméterrel
Optika:
Mikroszkóp okulárskálájának hitelesítése, hosszúságmérés mikroszkóppal
Fókusztávolság meghatározása távolságtörvény alapján
Optikai mérések Hartl-koronggal
Elektromosságtan:
Ohm-törvény vizsgálata
Ellenállások soros és párhuzamos kapcsolása
A fenti pályázat keretében elkészített tananyag az ismertetett tankönyv digitális és interaktív formában történő előállítását vállalta fel. Ezzel reményeink szerint nemcsak a korszerű tananyaggal szemben támasztott követelményeknek felel meg, hanem az egyre nagyobb számban jelentkező levelezőképzés igényeit is kiszolgálja.
Az új elektronikus tananyag tartalmazza
a tankönyv anyagát,
a kísérleti eszközök bemutatását,
a gyakorlatok kamerával való rögzítését,
feladatrészek megfogalmazását,
a tanult ismeretanyag ellenőrzését, vizsgadolgozatok, ismeretellenőrző feladatok és tesztgyűjtemény segítségével.
Tartalom
Az egyenletes mozgás vizsgálata, a sebesség meghatározása.
A buborék sebessége és a cső hajlásszöge közötti összefüggés vizsgálata.
Grafikonkészítés elemeinek megismerése (mm-papíron és számítógéppel).
A kísérleti eszköz névadója Mikola Sándor (1867-1945), matematika-fizika szakos tanár, a híres budapesti Fasori Gimnázium kiváló pedagógus-egyénisége, az MTA tagja, aki nagyon sokat tett a fizika kísérletes, gyakorlati oktatásának magyarországi megteremtéséért.
A Mikola-cső egy kb. 1 m hosszú, egyenes, állandó keresztmetszetű, egyik végén zárt üvegcső, amelybe vizet vagy színes folyadékot, pl. fluoreszceinnel festett vizet töltenek. Az üvegcső másik végét dugóval lezárják úgy, hogy a csőben egy kb. 2-3 cm hosszú buborék jöjjön létre. A buborék hidrodinamikai okok következtében a cső ferde állásában egyenletes mozgást végez.
Mint ismeretes, egyenes vonalú egyenletes mozgást végez az anyagi pont/test akkor, ha egyenes vonalú pályán ugyanabba az irányba halad, és egyenlő idők alatt egyenlő utakat tesz meg, bármilyen kicsik vagy nagyok is azok az egyenlő időközök. A test által megtett út (s) és az ezen út megtételéhez szükséges idő (t) között egyenes arányosság van, az arányossági tényező az egyenletes mozgásra jellemző mennyiség, az egyenletes mozgást végző test - esetünkben a buborék - sebessége (v):
(1.1)
.
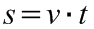A buborék mozgásának sebessége megváltozik, ha változtatjuk a Mikola-cső vízszintessel bezárt hajlásszögét(α), a legnagyobb sebességet kb. 45°-os hajlásszögnél tapasztaljuk.
A kísérleti eszközt szögmérővel látják el, így fok pontossággal változtatható a dőlésszög. Az üvegcső mögötti, az üvegcsőhöz rögzített mérőrúd skáláján a távolságok cm-es pontossággal olvashatók le.
Állítson be egy adott hajlásszöget, pl. 30 fokot, és mérje meg a 30 cm, 40 cm, 50 cm, 60 cm és 70 cm-es utak megtételéhez tartozó időket. Az időmérést akkor kezdje, amikor a buborék már nem a cső elején tartózkodik, hanem kb. 20 cm-t megtett a csőben. Az időmérést stopperórával végezze, és háromszor ismételje meg. Számolja ki a buborék sebességét. Vonjon le következtetéseket.
Változtassa a hajlásszöget, és mérje meg az 50 cm-es utak megtételéhez tartozó időket. Az időmérést itt is háromszor végezze el.
A mérési eredményeket foglalja táblázatokba, majd készítse el a megfelelő grafikonokat.
A grafikonkészítésnek az a célja, hogy gyors áttekintést nyújtson az egymással összefüggő fizikai mennyiségek közötti kapcsolatról. Akár mm-papíron, akár számítógéppel készítjük, a munka a derékszögű koordinátarendszer tengelyeinek megadásával kezdődik.
A tengelyeket irányítással kell ellátni, melyet tengely végénél nyíl mutat. A tengelyeken fel kell tüntetni az ábrázolt fizikai mennyiségek nevét (jelét) és azok mértékegységét. A vízszintes tengelyre a független változó értékei kerülnek, a függőleges tengelyre a függő változó értékei (általában). A tengelyeken jelölni kell az egységeket, egyenközű beosztásokkal. Az egységeket célszerűen kell felvenni, úgy, hogy a mérési eredmények a lehető legjobban tölthessék ki a grafikon területét.
A grafikont lássuk el címmel, dátummal. A grafikon címe lényegre utalóan informáljon a tartalomról. A mérési pontokat ne kössük össze, hanem szükség esetén illesszünk rájuk egyenest vagy görbét.
Igazolja méréssorozattal, hogy a ferdén tartott Mikola-csőben a levegőbuborék mozgása egyenletes!
Készítsen a buborék mozgásáról út-idő grafikont! Számolja ki a grafikon meredekségét! Milyen fizikai jelentése van a meredekségnek?
Határozza meg különböző dőlésszögek esetén (α = 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°) a buborék mozgásának sebességét!
Ábrázolja a sebességet a hajlásszög függvényében! Vonjon le következtetéseket, magyarázza meg a kapott eredményt!
Hogyan változik a buborék által megtett út az idő függvényében?
Hogyan függ a buborék sebessége a cső hajlásszögétől? Milyen grafikont kapott?
Hogyan igazolta a buborék egyenletes mozgását?
Definiálja az egyenes vonalú egyenletes mozgást!
Mondjon példát egyenes vonalú egyenletes mozgást végző testekre!
Mi a dinamikai feltétele az egyenes vonalú egyenletes mozgásnak?
A buborék azért mozog egyenletesen, mert nem hat rá erő.
A Mikola-cső névadója Mikola Sándor, matematika-fizika szakos tanár, aki a soproni Berzsenyi Dániel Líceumban is tanított.
A buborék a függőleges helyzetében már nem mozog egyenletesen.
Minél nagyobb a buborék, annál pontosabb a mérés.
Mikola-csővel jól tanulmányozható az egyenes vonalú egyenletesen gyorsuló mozgás.
Ha a buborék által megtett út függvényében ábrázoljuk az út megtételéhez szükséges időt, akkor a meredekség a sebességet adja meg.
Tartalom
A lejtőn mozgó test mozgásegyenletének alkalmazása, a hajlásszög szerepének tudatosítása.
A négyzetes úttörvény felismerése.
Linearizálás gyakorlása, a meredekség számítása és fizikai jelentésének elmélyítése.
A golyó mozgásának energetikai tárgyalása, a lejtőn leguruló golyó energiáinak vizsgálata.
Fémcsatornás lejtő (kb. 2 m hosszú), acélgolyók, stopperóra, mérőszalag, mm-papír.
2.1. ábra. Fémcsatornás lejtő.
A lejtőn történő mozgás tanulmányozásával Galilei (1564-1642) olasz fizikus foglalkozott először. Az ő mérései igazolták, hogy a lejtőn mozgó testnél a megtett út nem az idővel, hanem az idő négyzetével arányos. A 2006-ban amerikai fizikusok véleménye alapján összeállított minden idők legszebb tíz fizikai kísérletének listáján Galilei lejtős kísérlete a nyolcadik helyen szerepel.
A lejtőn elengedett test/leguruló golyó mozgása összetett. Tömegközéppontja a rá ható állandó erők (gravitációs erő, a felületre merőleges kényszererő, a lejtő irányú súrlódási erő) hatására egyenletesen gyorsuló mozgást végez. Eközben a golyó gyorsulva forog a tömegközéppontja körül.
A felírható mozgásegyenletek:
(2.1)
,
(2.2)
,
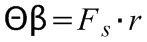(2.3)
,
itt nem részletezendő megoldása után megállapítható, hogy a lejtőn mozgó golyó egyenletesen gyorsuló mozgást végez (a = áll.).
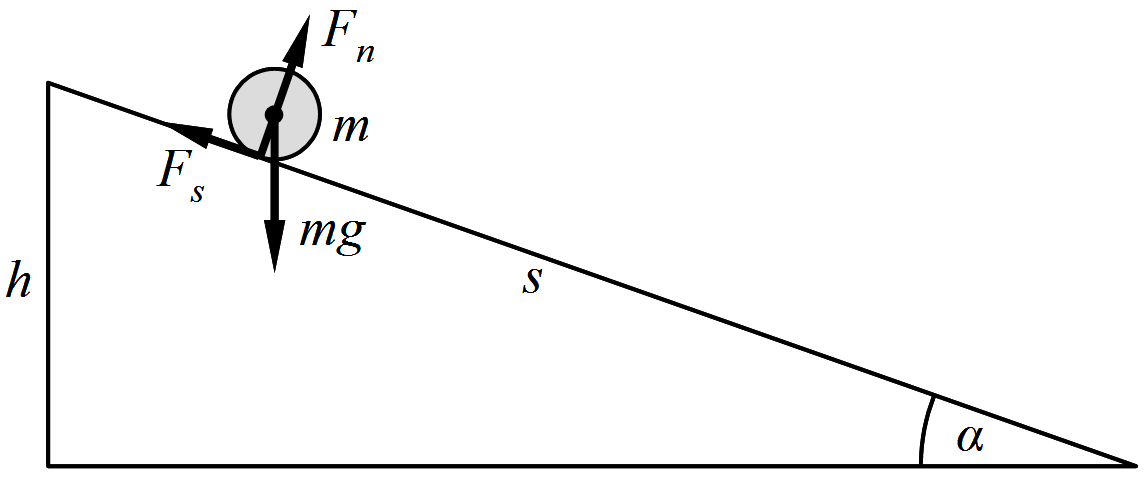
2.2. ábra. A lejtőn leguruló golyóra ható erők.
Ha a kezdősebesség nélkül elindított golyó (lásd a 2.2. ábrát) az s hosszúságú lejtőn a gyorsulással t ideig mozog, akkor a megtett útja az
(2.4)
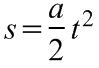
összefüggéssel, a lejtő alján a sebessége pedig a
(2.5)
formulával adható meg.
Mozgási energiája a lejtő alján két részből tevődik össze. Egyrészt a haladó mozgás mozgási energiájából:
(2.6)
,
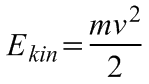másrészt a tömegközéppont körüli ω szögsebességű forgás forgási energiájából:
(2.7)
.
A (2.7) összefüggésben Θ = 2/5ˇmr2 az m tömegű, r sugarú golyónak a tömegközéppontján átmenő tengelyre vonatkozó tehetetlenségi nyomatéka. Felhasználva a csúszás nélküli, ún. tiszta gördülésre vonatkozó v = rˇω feltételt, a mozgási energiák összegére
(2.8)
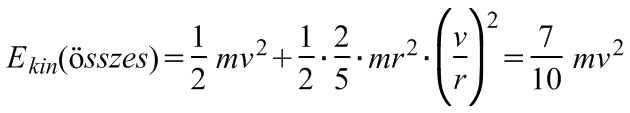
adódik. A munkatételből következik, hogy a mozgási (kinetikus) energiák megváltozása egyenlő a gravitációs erő munkájával - mivel a nyomóerőnek és tiszta gördülésnél a súrlódási erőnek nincs munkavégzése -, azaz a gravitációs helyzeti energia csökkenésével:
(2.9)
,
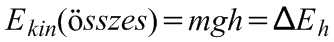ahol h a lejtő magassága.
A beállított hajlásszögű fémcsatornában egy acélgolyót indítunk el, amely egy alkalmasan elhelyezett ütközőig mozog, ott kattanó hangot hallat.
Állítson be az állítható hajlásszögű fémcsatornás (alumínium) lejtőn a négyzetes úttörvénynek megfelelően 10 cm, 40 cm, 90 cm, 160 cm-es utakat. Mérje meg stopperórával a megfelelő távolságok megtételéhez szükséges időket. Minden mérést ötször végezzen el.
Számítsa ki az idők átlagait. Hogyan aránylanak egymáshoz az eltelt idők? Vonjon le következtetést. Adatait foglalja táblázatba.
Igazolja, hogy a lejtőn leguruló golyó mozgása egyenletesen gyorsuló! Milyen függvényt vár? Vonjon le következtetést a lejtőn mozgó test mozgására vonatkozóan!
Ábrázolja a megtett utakat a megtételükhöz tartozó idők függvényében!
Ábrázolja a megtett utakat az idők négyzetének függvényében, azaz linearizálja az s = (a/2)t2 összefüggést! Milyen grafikont vár? Elemezze és értelmezze a kapott grafikont!
Határozza meg a harmadik feladatban kapott grafikon meredekségét! Milyen fizikai jelentése van a meredekségnek? Határozza meg a meredekségből a gyorsulás értékét!
Hasonlítsa össze a lejtő alján a golyó haladó mozgásához tartozó mozgási energiát a forgó mozgásában tárolt energiával! Számolja ki a helyzeti energia csökkenését! Határozza meg a kinetikus energia és a helyzeti csökkenésének százalékos arányát! Magyarázza meg tapasztalatait!
Állítson be az előzőtől különböző hajlásszögű lejtőt, és ismételje meg a méréssorozatot! Eredményeit foglalja újabb táblázatba!
Hogyan változik a lejtőn mozgó test által megtett út az idő függvényében?
Milyen görbét kap, ha az idő négyzetének függvényében ábrázolja a megtett utat?
Mi a linearizálás lényege?
Hogyan határozta meg grafikus úton a lejtőn leguruló golyó gyorsulását?
A lejtőn leguruló golyó teljes mozgási energiájának hány százaléka származik a haladó mozgásból és hány százaléka a forgó mozgásból? Válaszát a megfelelő formulák felhasználásával indokolja (csúszás nélküli, tiszta gördülést feltételezve)!
Mi a dinamikai feltétele az egyenes vonalú egyenletesen gyorsuló mozgásnak?
A lejtőn mozgó testek tanulmányozásával először Galilei foglakozott.
A Galilei-lejtőn négy csatornában golyók gurulnak, és egyenlő idők alatt egyenlő utakat tesznek meg.
A lejtőn guruló golyók mozgását ugyanúgy a négyzetes úttörvény írja le, mint a szabadon eső testekét.
Ha független változónak az idő négyzetét, függő változónak az utat választjuk, akkor az egyenes meredeksége a gyorsulást adja meg.
A golyó gyorsulása független a lejtő hajlásszögétől.
A linearizálás azt jelenti, hogy olyan mennyiségeket ábrázolunk a tengelyeken, amelyek egymással egyenesen arányosak.
Tartalom
Kényszermozgás vizsgálata, értelmezése inercia-rendszerben.
A dinamika alapegyenletének alkalmazása.
Egyenletesen gyorsuló mozgás megfigyelése, útképletének használata.
Leybold gyártmányú Atwood-ejtőgép, tartozékokkal: M = 2x70 g, 4x98 g tömegek, m = 2 g, 4 g, 6 g mozgató tömegek, stopperóra, mérőszalag.
3.1. ábra. Atwood-féle ejtőgép.
A készülék megalkotója George Atwood, angol matematikus és fizikus, a Cambridge-i Trinity College tanára, aki 1784-es értekezésében említi először a készüléket, amely - helyettesítve Galilei lejtőjét - a nehézségi gyorsulás pontos meghatározására készült.
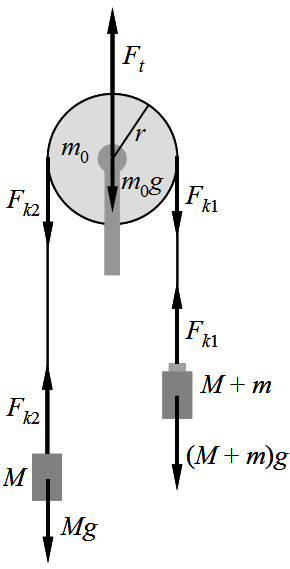
3.2. ábra. Az Atwood-féle ejtőgép mozgását meghatározó erőrendszer.
Az Atwood-féle ejtőgéppel egyenes vonalú, egyenletesen változó mozgást állíthatunk elő, különböző tömegű mozgatott testek és különböző nagyságú mozgató erők esetén. Az eszköz alkalmas az egyenletesen változó mozgás, valamint az erő és a mozgatott tömeg közötti kapcsolat (dinamika alapegyenlete) vizsgálatára.
Mozgatott tömegnek kell tekinteni a csigán átvetett zsinór két végén függő egy-egy M tömegű testet, a mozgató erőt is képviselő m tömeget, valamint a csiga m0 tömegét. E három test mozgására írjuk fel a haladó- és a forgómozgásra vonatkozó dinamika mozgásegyenleteit:
(3.1)
,
(3.2)
,
(3.3)
Fk1 és Fk2 a kötelekben ébredő erők, r a csiga sugara, Θ a csiga forgástengelyre vonatkozó tehetetlenségi nyomatéka, β = a/r (tiszta gördülést feltételezve) a csiga szöggyorsulása. Ezekből a dinamikai egyenletekből az a gyorsulás meghatározható:
(3.4)
.
Ugyancsak meghatározható a gyorsulás kinematikai úton, az egyenletesen gyorsuló mozgás
(3.5)
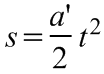
útképletének felhasználásával. A készüléken kényelmesen változtatható az út hosszúsága, és a speciális indítószerkezet lehetővé teszi a pontos, mechanikus időmérést. A kétféle módon nyert gyorsulás egyenlősége a dinamika alapegyenletének teljesülését jelenti.
A mérések megkezdése előtt a csigán a fonalak súrlódását kis, ún. póttömegek segítségével gondosan ki kell küszöbölni! Ehhez hozzuk mozgásba a testeket, és figyeljük meg, hogy egyenletesen mozognak-e. Ha nem, akkor alkalmazzunk póttömeget, majd teszteljük újra a mozgást, és szükség esetén végezzük tovább a korrekciót.
állványon közel súrlódás nélkül forgó csiga
csigán átvetett, súlytalannak tekintett fonal, végén egyenlő tömegekkel (M) és egyik végén kis túlsúllyal (m)
mérőrúd (az állvány része), 10 cm-es beosztással
mechanikus indítószerkezet
Tanulmányozza az összeállított kísérleti berendezést!
Állítson be s = 1 m-es utat és M = 70 g tömeget, majd változtatva a gyorsító nehezék tömegét: m = 2, 4, 6 g, mérje meg az út megtételéhez szükséges időket! A mérést ötször ismételje meg! Számoljon időátlagot, majd ennek segítségével számolja ki a gyorsulást (a') az útképlet felhasználásával, a 3.5 egyenlet szerint!
Számolja ki a gyorsulást (a) a dinamika alapegyenletének felhasználásával is, a 3.4 egyenlet szerint! A csiga tömege, m0 = 100 g.
A kapott eredményeket hasonlítsa össze, számolja ki a δrel = (a'-a)/a relatív eltérésüket!
Ismételje meg a mérést úgy, hogy M értékét 70 g + 98 g-ra növeli! A súrlódást újra küszöbölje ki, eredményeit foglalja újabb táblázatba!
Adja meg a kísérleti elrendezés sematikus rajzát!
Írja fel a testek mozgásegyenleteit, és határozza meg a testek gyorsulását!
Hogyan határozza meg mérésekkel a testek gyorsulását?
Mérései során hogyan küszöböli ki a testek mozgását zavaró súrlódást?
Hogyan igazolja a dinamika alapegyenletének helyességét az Atwood-féle ejtőgéppel?
Hogyan befolyásolja a gyorsulás értékét a csiga tömege?
Az Atwood-féle ejtőgép megalkotója amerikai származású fizikus és matematikus.
Az Atwood-féle ejtőgéppel tanulmányozható az egyenes vonalú egyenletes és az egyenes vonalú egyenletesen gyorsuló mozgás is.
Az Atwood-féle ejtőgép esetén felírt mozgásegyenletekben a csiga tömegét sohasem kell figyelembe venni.
A testek gyorsulása a négyzetes úttörvény szerint számolható.
Mérései során a testek mozgását zavaró súrlódást póttömegekkel lehet kiküszöbölni.
Az Atwood-féle ejtőgéppel a dinamika alapegyenletének helyessége igazolható.
Tartalom
A nehézségi gyorsulás meghatározása különböző hosszúságú fonálingák lengésidejének mérésével.
A grafikonkészítés gyakorlása, linearizálás, a meredekség fizikai jelentésének felhasználása.
Változtatható hosszúságú fonálinga, Bunsen-állvány, mérőszalag, tolómérő, stopperóra, mm-papír.
4.1. ábra. Matematikai inga.
Az egyik végén rögzített, elhanyagolható tömegű, hosszú, nyújthatatlan fonálból és a végére erősített viszonylag nagy tömegű nehezékből álló testet fonálingának nevezzük. Ha a nehezék mérete elhanyagolható a fonál hosszához képest, matematikai ingáról van szó, amely egyensúlyi helyzetéből kimozdítva, majd elengedve kis kitérések esetén harmonikus rezgőmozgást végez. A rezgőmozgást a testre ható mg nehézségi erő (szabaderő) és a fonalban ébredő Fk kényszererő eredője (lásd a 4.2. ábrát) biztosítja.
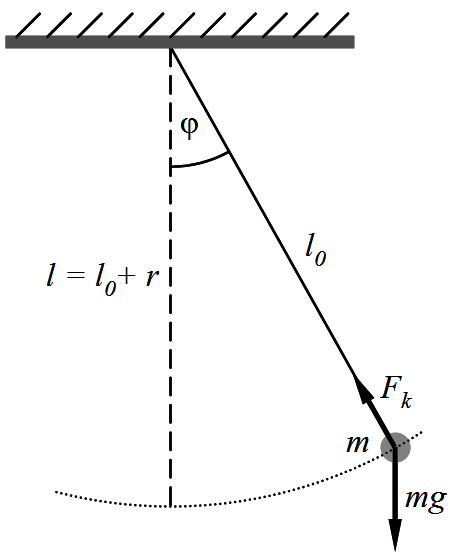
4.2. ábra. A matematikai inga mozgását meghatározó erők.
Az eredő erő a mozgás során jó közelítéssel az egyensúlyi helyzet irányába mutat, és nagysága arányos az egyensúlyi helyzettől mért távolsággal. A harmonikus rezgőmozgás T periódusideje kis kitérések esetén (φ < 5ş) csak az inga hosszától (l) és a g nehézségi gyorsulástól függ, az alábbi képlet szerint:
(4.1)
.
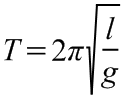A fonálinga hosszán a felfüggesztési pont és az inga tömegközéppontjának távolságát kell érteni. A periódusidő az az időtartam, amíg az inga az egyik szélső helyzetből indulva 1 teljes lengést megtéve ugyanoda visszatér. A (4.1) összefüggés alapján a nehézségi gyorsulás számítható:
(4.2)
.
Az összefüggésből látható, hogy a T 2 egyenes arányban áll az inga hosszával, az arányossági tényező - vagyis a T 2(l) függvény meredeksége - a 4π2/g kifejezés. A g értéke tehát grafikus ábrázolás után a meredekségből is meghatározható. Ezt az eljárást, amikor a lengésidő (4.1) formuláját célszerűen úgy alakítjuk át, hogy az ábrázolt mennyiségek között lineáris legyen a kapcsolat, linearizálásnak nevezzük.
Pontosabb számításhoz a nehezék geometriai méretét és tömegeloszlását is figyelembe kell venni, ilyenkor ún. fizikai ingáról beszélünk, amelynek periódusideje:
(4.3)
.
Θ a rendszer tehetetlenségi nyomatéka az inga felfüggesztési pontján átmenő vízszintes tengelyre vonatkozóan. Az összefüggésben s a forgástengely és az inga tömegközéppontjának távolságát jelenti.
Különböző fonalhosszaknál mérje meg az inga lengésidejét. Ehhez 10 teljes lengés idejét mérje össze, majd a mért összidőt ossza el tízzel. A mérést háromszor ismételje meg. Mivel a (4.1) formulában az ingahossz a forgástengely, illetve a felfüggesztési pont és az inga tömegközéppontjának a távolságát jelenti, ezért l az l0 fonálhossz és a nehezékként használt fémgolyó r sugarának az összegével egyenlő:
(4.4)
.
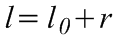A fonálhosszat mérőszalag segítségével határozza meg, a vasgolyó sugarát (d átmérőjét) tolómérővel mérje. Az így kapott adatokat a táblázatban való rögzítés előtt többször ellenőrizze.
Az inga indításánál az ingának kis amplitúdójú kitérést adjon - a kitérés szöge 5°-nál ne legyen nagyobb - engedje el, és ügyeljen arra, hogy az inga síkmozgást végezzen.
A (4.2) összefüggés alapján, az ingahosszak és a hozzájuk tartozó periódusidők ismeretében számolja ki a nehézségi gyorsulás értékeket, majd ezek átlagát! Adja meg az eredmények szórását is!
Ábrázolja a periódusidők négyzetét az ingahosszak függvényében! Határozza meg a kapott egyenes meredekségét, majd ez alapján is számítsa ki a nehézségi gyorsulás értékét!
Adja meg a (4.2) formulával meghatározott nehézségi gyorsulások átlagának, valamint a grafikus módon meghatározott nehézségi gyorsulásnak az irodalmi értéktől való relatív eltérését: δrel = (g-girod)/girod! Értelmezze a kapott eredményt!
Hogyan függ a nehézségi gyorsulás értéke az inga hosszától?
Hogyan függ a nehézségi gyorsulás értéke az inga kitérésétől?
Milyen mozgást végez a matematikai inga?
Rajzolja fel a testre ható erőket, írja fel a mozgásegyenleteket és oldja meg kis kitérésekre!
Hogyan határozható meg grafikusan a nehézségi gyorsulás értéke?
Mi az izokronizmus? Ki állapította meg ezt a tényt először?
A matematikai inga mindig síkingaként mozog.
A matematikai inga mozgása rezgőmozgás.
A matematikai inga kis kitéréseknél harmonikus rezgőmozgást végez.
A matematikai inga hosszának meghatározásakor a golyó sugarát elhanyagolhatjuk.
A nehézségi gyorsulás grafikus meghatározása linearizálással lehetséges.
Az izokronizmus jelenségével először Newton foglakozott.
Tartalom
A fizikai inga jellemzőinek megismerése.
Fémtárcsa (korong) tehetetlenségi nyomatékának meghatározása.
Steiner tételének alkalmazása.
Súlypontjában alátámasztott fizikai inga, tárcsára csavarozható hengerek a súlypont változtatásához, vonalzó, stopperóra, digitális mérleg.
5.1. ábra. Vízszintes tengely körül forgatható tárcsa póttömeggel, mint fizikai inga.
Jakob Steiner (1796-1863) alapvetően matematikával, ezen belül is legfőképp geometriával foglalkozott, svájci származású, Berlinben működő egyetemi tanár volt. Nevéhez fűződik a lényegében geometriai jellegű megfontolásokon alapuló Steiner-tétel, amely a súlyponti és azzal párhuzamos tengelyekre vonatkozó tehetetlenségi nyomaték számításakor alkalmazható.
A fizikai inga olyan merev test, amely rögzített, vízszintes tengely körül foroghat a nehézségi erő hatása alatt. Legyen a test S súlypontján átmenő és a forgástengelyre merőleges sík az 5.2. ábra síkja, a tengelynek ezzel való döfési pontja O. Jelöljük az
távolságot s-sel, a forgástengelyre vonatkozó tehetetlenségi nyomatékot Θ-val.
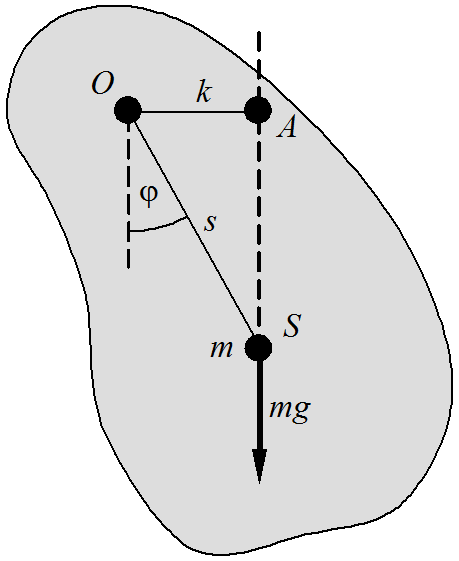
5.2. ábra. Jelölések a fizikai inga lengési idejének kiszámolásához.
Ha az ingát stabilis egyensúlyi helyzetéből (az S súlypont az O alátámasztási pont alatt van!) φ szöggel kitérítjük, azaz az OS egyenes a függőlegessel φ szöget zár be, akkor az 5.2. ábra alapján a nehézségi erő
(5.1)
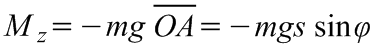
forgatónyomatékot gyakorol az ingára. Így a mozgásegyenlet:
(5.2)
,
vagy átrendezve
(5.3)
.
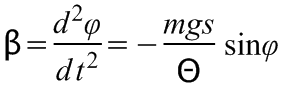Ezt a matematikai inga
(5.4)
alakú mozgásegyenletével összehasonlítva látható, hogy a fizikai inga ugyanúgy leng, mint egy
(5.5)
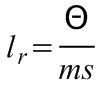
hosszúságú matematikai inga, tehát kis kitérések, amplitúdók esetén a fizikai inga lengésideje:
(5.6)
;
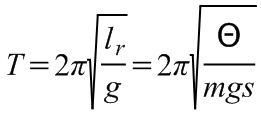nagyobb amplitúdóknál pedig korrekció alkalmazandó. Az lr mennyiséget a fizikai inga redukált hosszának nevezzük.
Ismeretes, hogy a fizikai inga mint merev test adott O tengelyre vonatkozó tehetetlenségi nyomatékán a test tömegeloszlásától függő
(5.7)
pozitív mennyiséget értjük, ahol li az mi tömegű pontnak a O tengelytől (a forgástengelytől) mért távolsága. Kimutatható, hogy egy homogén tömegeloszlású, körhenger (tárcsa, korong) tehetetlenségi nyomatéka a síkjára merőleges szimmetriatengelyére vonatkozóan:
(5.8)
,
ahol M a körhenger tömege, R pedig a sugara.
Ha a forgástengely nem a szimmetriatengely, de azzal párhuzamos, akkor az erre a tengelyre vonatkozó tehetetlenségi nyomaték a Steiner-tétellel számítható ki:
(5.9)
,
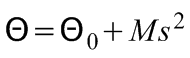ahol s a két párhuzamos tengely egymástól mért távolsága.
A gyakorlaton kiadott tárcsát, amely a középpontján átmenő vízszintes tengely körül elfordulhat, állványba fogtuk. Tömege (M) ismeretlen. A tárcsát gondosan kiegyensúlyoztuk, azaz éppen súlypontjában van alátámasztva, így közömbös (indifferens) egyensúlyi helyzetben van. A tárcsába, annak egyik átmérője mentén, a tengelytől meghatározott l távolságokra kisméretű lyukakat fúrtunk.
A tárcsa Θ0 tehetetlenségi nyomatékát úgy határozhatjuk meg, hogy a tárcsán levő egyik lyukba kisméretű, m tömegű hengert, póttömeget csavarozunk. Így egy M+m tömegű fizikai ingát kapunk, amelynek lengésideje mérhető. Kis kitérések mellett ekkor fennáll, hogy
(5.10)
,
ahol Θ a tárcsa (mint fizikai inga) adott (O) forgástengelyre vonatkozó tehetetlenségi nyomatéka, amely additív módon tehető össze a tárcsa Θ0 , állandó és a póttömegül szolgáló henger változó, a távolságtól függő Θ h tehetetlenségi nyomatékából. Ha a tárcsára szerelt m tömegű hengert pontszerű (vonalszerű) testnek tekintjük, akkor
(5.11)
,
ahol l a henger középpontjának a forgástengelytől mért távolsága. Ha a hengert nem tekinthetjük pontszerűnek, akkor - az O tengelyre vonatkozó - tehetetlenségi nyomatéka a Steiner-tétel alkalmazásával pontosítható:
(5.12)
,
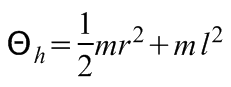ahol r a henger sugara.
A feladat első lépéseként határozzuk meg a tárcsa-henger rendszer s tömegközéppontjának a forgástengelytől (a tárcsa középpontjából) mért
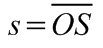távolságát!
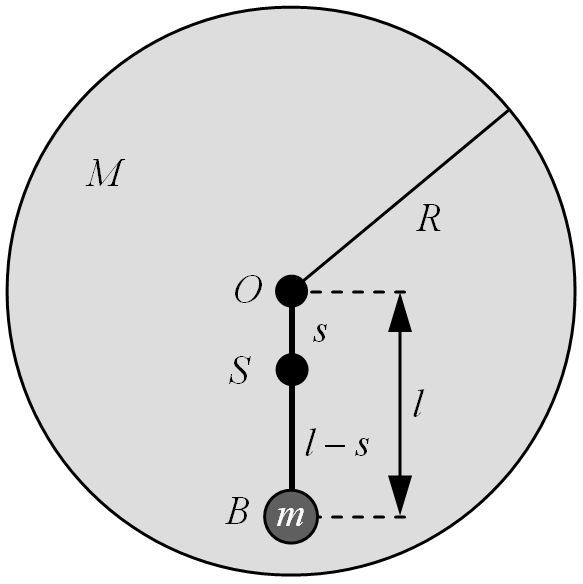
5.3. ábra. Jelölések a póttömeggel ellátott tárcsa lengési idejének kiszámolásához.
Az 5.3. ábra alapján fennáll, hogy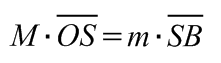 
, ahol 
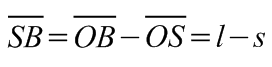, így
(5.13)
.
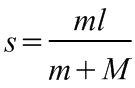A (5.10), (5.11) és (5.13) összefüggések felhasználásával a lengésidőre a
(5.14)
összefüggés adódik, és mint látható, M nem szerepel az összefüggésben. A (5.14) összefüggés átrendezésével kapjuk, hogy:
(5.15)
.
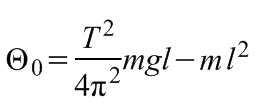Tehát a tehetetlenségi nyomaték meghatározásához a felcsavarozható hengerek forgástengelytől való távolságát és tömegét kell ismerni, illetve periódusidőt kell mérni.
Becsülje meg a geometriai méretek felhasználásával a tárcsa tehetetlenségi nyomatékát a középpontján átmenő, vízszintes tengelyre vonatkozóan! A tárcsa anyagának sűrűsége 7800 kg/m3.
Mérje meg a kiadott r sugarú henger tömegét digitális mérleggel!
Csavarozza a hengert a tárcsa egyes lyukaiba (l értékeit változtatva), és mérje meg a létrejött fizikai inga lengésidejét - kis kitérés mellett - több lengésidő együttes méréséből! Adatait foglalja táblázatba!
A (5.15) összefüggés felhasználásával számítsa ki a tárcsa Θ0 tehetetlenségi nyomatékát!
Adja meg az eredmények szórását is!
Hasonlítsa össze a becsléssel és a méréssel kapott Θ0 tehetetlenségi nyomaték értékeket! Számoljon relatív eltérést!
Mikor kapunk egy merev testből fizikai ingát? (Mi a fizikai inga?)
Írja fel a fizikai inga mozgásegyenletét, és oldja meg kis kitérésekre!
Adja meg a fizikai inga lengésidejére vonatkozó összefüggést! Nevezze meg a benne szereplő fizikai mennyiségeket!
Mit értünk a fizikai inga redukált hosszán, és hogyan számolható ki?
Definiálja a tehetetlenségi nyomatékot!
Fogalmazza meg Steiner tételét!
A fizikai inga egy merev test, amely nem a súlypontjában van alátámasztva, ezért a nehézségi erő hatására lengéseket végezhet.
A tehetetlenségi nyomaték nem függ a test tömegeloszlásától.
A Steiner-tétel egymásra merőleges tengelyekre vonatkozó tehetetlenségi nyomatékok között ad meg összefüggést.
A fizikai inga lengésidejére vonatkozó összefüggésben a forgástengelynek és a súlyvonalnak a távolsága szerepel.
Egy adott fizikai inga redukált hossza megmutatja, hogy milyen hosszúságú matematikai ingával egyezik meg a periódusideje.
Pontos mérések és számítások esetén a számolt tehetetlenségi nyomaték nagyobb, mint a ténylegesen mért tehetetlenségi nyomaték.
Tartalom
A négyzetes úttörvény felismerése, a szöggyorsulás meghatározása.
A rögzített tengely körül forgó test mozgásegyenletének alkalmazása.
Linearizálás gyakorlása, a meredekség számítása és fizikai jelentésének elmélyítése.
A kísérleti eszköz (lásd a 6.1 ábrát) és tartozékai, 10 g-os súlysorozat (tömeg-sorozat), mérőszalag, stopperóra.
6.1. ábra. A forgómozgás tanulmányozására szolgáló kísérleti eszköz.
Ha a rögzített tengely körül forgó merev testre állandó nagyságú M forgatónyomaték hat, akkor a test egyenletesen gyorsuló forgómozgást végez. A szögelfordulásra érvényes a következő összefüggés:
(6.1)
,
ahol φ a radiánokban mért szögelfordulás, β a szöggyorsulás radián/s2-ben, t a φ szögelforduláshoz szükséges idő.
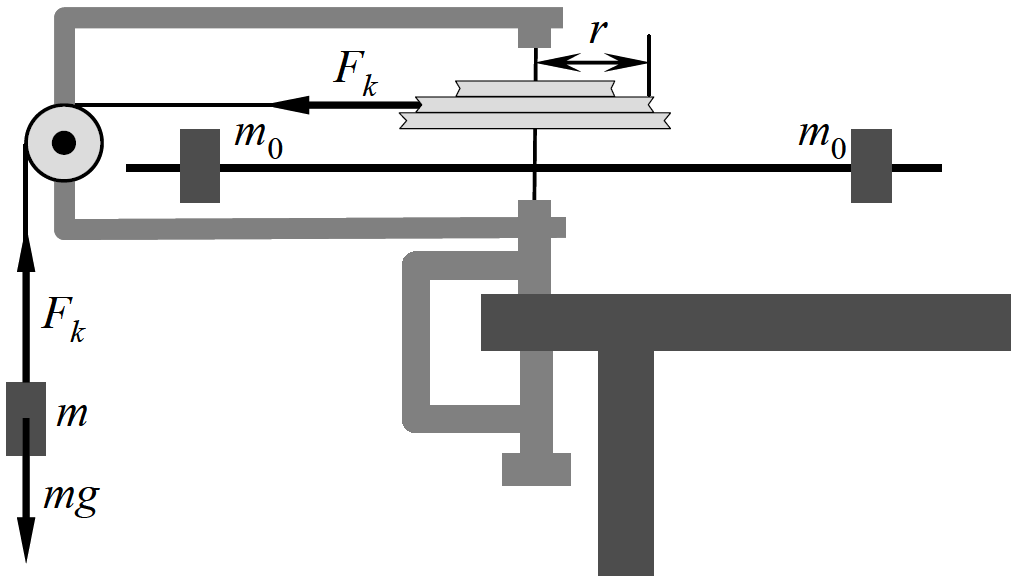
6.2.ábra. A rendszerre ható erők.
A forgómozgásra felírt mozgásegyenlet szerint a szöggyorsulást adott forgatónyomaték mellett a forgó rendszer forgástengelyre vonatkozó tehetetlenségi nyomatéka (Θ) befolyásolja az alábbi egyenlet szerint:
(6.2)
.
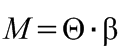Az alkalmazott kísérleti berendezésen változtatható a forgatónyomaték, mind az erőkaron (r), mind az Fk erőn keresztül. Ezen kívül változtatható a forgó rendszer tehetetlenségi nyomatéka mind a forgó tömeg (az ábrán m0 jelöli), mind annak forgástengelytől való távolsága (l) segítségével; mint ismeretes, a tehetetlenségi nyomaték definíció szerint:
(6.3)
.
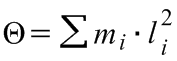Állítson be adott forgatónyomatékot és adott tehetetlenségi nyomatékot, és mutassa meg, hogy a rendszer egyenletesen gyorsuló mozgást végez! Ehhez mérje meg a π, 2π, 3π, 4π, 5π, 6π, 7π, 8π szögelfordulásokhoz szükséges időket! Minden mérést háromszor végezzen el! Adatait foglalja táblázatba! Számítsa ki az idők átlagait, és az átlagidők négyzeteit!
Ábrázolja a megtett szögelfordulásokat a megtételükhöz tartozó idők függvényében! Milyen függvényt vár? Vonjon le következtetést a rögzített tengely körül forgó test mozgására vonatkozóan!
Ábrázolja a megtett szögelfordulásokat az idők négyzetének függvényében! Milyen grafikont vár? Elemezze és értelmezze a kapott grafikont!
Határozza meg a 3. feladatban kapott grafikon meredekségét! Milyen fizikai jelentése van a meredekségnek?
Határozza meg a meredekségből a szöggyorsulás értékét!
Növelje meg az M = Fk r = m (g-a) r forgatónyomatékot - amely közelítőleg mgr -rel egyenlő (mivel a Ť g) - a gyorsulást létrehozó tömeg változtatásával közel kétszeresére, háromszorosára, négyszeresére és ötszörösére! A rendszer tehetetlenségi nyomatékát az előzőhöz képest ne változtassa! Mérje meg egy adott, pl. 4π szögelfordulásokhoz tartozó időket! Az adatokat foglalja táblázatba!
Ábrázolja a forgatónyomatékokat (önkényesen választott egységekben) a β-val arányos (1/t)2 függvényében! Elemezze a kapott eredményt!
Mely más mennyiség mérését teszi lehetővé ez az eszköz?
6.1. táblázat - Táblázat az 1. feladat mérési eredményeihez.
|
φ (rad) |
π |
2π |
3π |
4π |
5π |
6π |
7π |
8π |
|---|---|---|---|---|---|---|---|---|
|
t1 (s) |
|
|
|
|
|
|
|
|
|
t2 (s) |
|
|
|
|
|
|
|
|
|
t3 (s) |
|
|
|
|
|
|
|
|
|
tátl (s) |
|
|
|
|
|
|
|
|
|
(tátl)2 (s2) |
|
|
|
|
|
|
|
|
Mit ért tengelyre vonatkozó forgatónyomaték alatt?
Definiálja a szögsebességet és a szöggyorsulást!
Rajzolja fel a rendszerre ható erőket, és írja fel az m tömegű nehezék és a rögzített tengely körül forgó merev test mozgásegyenleteit!
Hogyan változik a forgó test szögelfordulása az idő függvényében?
Milyen görbét kap, ha az idő négyzetének függvényében ábrázolja az elfordulás szögét?
Hogyan határozza meg a mérési eredményekből a szöggyorsulást?
Az egyenletesen gyorsuló forgómozgásra vonatkozó útképlet: φ=(β/2)t2 , ahol φ a szögelfordulás, β a szöggyorsulás, t az idő.
A tengely körüli forgómozgás alapegyenlete szerint az alkalmazott forgatónyomatékkal arányos szöggyorsulás jön létre.
Ha a szögelfordulást az idő függvényében ábrázoljuk, akkor parabola ívet kapunk.
A kísérleti eszköz alkalmas gömb, henger, hasáb tehetetlenségi nyomatékának kísérleti úton történő meghatározására.
Ha a forgatónyomatékot az idő függvényében ábrázoljuk, akkor a görbe meredeksége a tehetetlenségi nyomatékot adja meg.
A tehetetlenségi nyomaték mindig adott tengelyre vonatkozik és csak a tömegtől függ.
Tartalom
Az ideális gáz összetartozó nyomás, térfogat és hőmérséklet értékei alapján az ideális gáztörvény igazolása.
A gáz (anyag)mennyiségének meghatározása.
A grafikus ábrázolás, a meredekség meghatározásának gyakorlása.
A 7.1. ábrán látható kísérleti eszköz összeszerelt állapotban, termosztát, aneroid barométer, vonalzó, mm-papír.
7.1. ábra. A gázok állapotegyenletének tanulmányozására szolgáló kísérleti eszköz.
Ideális gáznak azokat a gázokat tekintjük, melyeknél a gázrészecskék saját térfogata elhanyagolható a tároló edény térfogatához képest, a részecskék közötti kohéziós erők elhanyagolhatók, ütközésük egymással és az edény falával rugalmasnak tekinthető. Ideális gázok esetén az állapotjelzők között a következő kapcsolat írható fel, ezt állapotegyenletnek nevezzük:
(7.1)
,
illetve
(7.2)
,
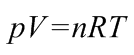ahol p a gáz nyomása, V a gáz által kitöltött térfogat, T az abszolút hőmérséklet, N a gázrészecskék száma, k a Boltzmann-állandó, n a gáz anyagmennyisége, R az egyetemes gázállandó.
A kísérleti eszköz egy, az egyik végén zárt U alakú üvegcső, melyhez alul, egy gumicsövön keresztül tartókehely csatlakozik. (Lásd a 7.1. és 7.2. ábrákat.) Az üvegcsőben és a kehelyben higany van. A higany zárja el a vizsgálandó levegőt a zárt szárban oly módon, hogy a tartókehely függőleges mozgatásával a levegő térfogata és nyomása is változtatható. A levegőt tartalmazó üvegcső mm-es beosztású. Mivel a cső 1 cm2 keresztmetszetű és cm-es beosztású, ezért a térfogat cm3 egységekben olvasható le. A levegő hőmérsékletét egy termosztát segítségével ún. vízfürdőn keresztül állítjuk be, illetve változtatjuk, mert ahogy az a 7.2. ábrán látszik, a gázt folyadékköpeny veszi körül, amely áramlásba hozható.
7.2. ábra. A készülék elvi felépítése.
A bezárt levegő nyomása a p0 külső légnyomásnak és a Δh higanyszintkülönbséghez tartozó hidrosztatikai nyomásnak az összege:
(7.3)
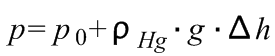
(g a nehézségi gyorsulás, ρ Hg a higany sűrűsége).
Határozza meg a 30-60 şC intervallumban, 5 şC-onként a bezárt gáz nyomását és térfogatát. Ehhez a Δh higanyszint-különbséget és az üvegcső gázzal telt részének a hosszát kell lemérni. A hőmérsékletet a termosztát hőmérőjén olvassa le, minden új hőmérséklet állításnál várjon pár percet, amíg a hőmérsékleti egyensúly közelítőleg beáll. A külső légnyomás értékét a kiadott aneroid barométerről olvassa le. Mérési adatait foglalja táblázatba.
Minden hőmérsékleten (30-60 şC) adja meg az összetartozó nyomás- és térfogatértékek szorzatát! Határozza meg minden hőmérsékleten a pV/T hányadost! Magyarázza meg a kapott eredményt! A higany sűrűsége, ρHg = 13600 kg/m3.
Ábrázolja a pV szorzatokat a T függvényében! Határozza meg a kapott egyenes meredekségét!
A meredekségből számolja ki a bezárt gáz részecskeszámát és anyagmennyiségét. k = 1,38ˇ10 -23 J/K, R = 8,31 J/(molˇK)!
Mit nevezünk ideális gáznak?
Fogalmazza meg az ideális gázokra vonatkozó állapotegyenletet, nevezze meg a benne szereplő mennyiségeket!
Hogyan határozta meg a kísérletben a bezárt levegő nyomását?
Hogyan határozta meg a kísérletben a bezárt levegő mennyiségét (mólszám és részecskeszám)?
Hogyan biztosítja a vizsgált gáz állandó hőmérsékletét?
Adja meg a nem ideális gázok viselkedését leíró Van der Waals-féle állapotegyenletet!
Az ideális gáz egy modell, valójában nem létezik.
Az anyagmennyiség az SI-ben alapmennyiség, mértékegysége a kilogramm.
Az ideális gáz állapotegyenlete az állapotjelzők közötti kapcsolatot írja le.
A pV = f (T) függvény meredeksége a gázállandót adja meg.
Ideális gázoknak csak a nemesgázok tekinthetők.
A termosztáttal a vizsgált gáz hőmérsékletét lehet beállítani és állandó értéken tartani.
Tartalom
A légnyomás meghatározása a Boyle-Mariotte törvény alapján.
Hidrosztatikai nyomás számításának gyakorlása.
A kísérleti eszköz névadója Franz Emil Melde (1864-1901), aki a németországi Marburg egyetem oktatója volt, s aki nagyon sok tudományos igényű demonstrációs eszköz kifejlesztésével és megépítésével gazdagította a fizikát. Tudományos érdemeit a folyadékmechanika, az elektromosságtan és a meteorológia mellett leginkább a hangtan területén szerezte. A Chladni-ábrákról szóló tanulmánya, hangszeres kísérletei (Melde maga is gyakorló zenész és zenekedvelő volt), ultrahanggal kapcsolatos vizsgálatai komoly nemzetközi elismerést is szereztek számára.
A Melde-cső egy vékony, mindenütt azonos keresztmetszetű, kb. 50 cm hosszú üvegcső, melynek egyik vége zárt. A csőben közel súrlódás nélkül mozgó x hosszúságú higanyoszlop levegőt zár el (Lásd a 8.2. ábrát).
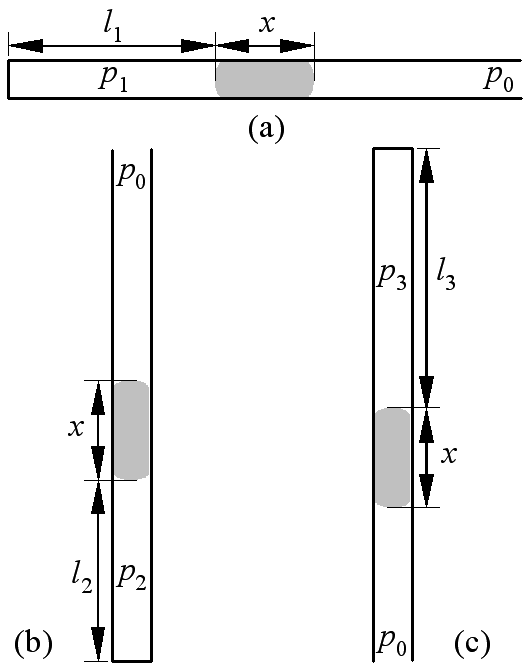
8.2. ábra. A Melde-cső különböző helyzetekben.
Ha a csövet vízszintesen tartjuk, a bezárt levegő p1 nyomása megegyezik a p0 külső légnyomással. Ha a csövet nyitott véggel felfelé állítjuk, a bezárt levegő p2 nyomása a külső légnyomás (p0) és a higanyoszlop hidrosztatikai nyomásának (pHg az összegével, ha nyitott véggel lefelé tartjuk, a gáz p3 nyomása ezek különbségével egyenlő:
(8.1)
,
, és 
A Boyle-Mariotte törvény értelmében az állandó anyagmennyiségű és állandó hőmérsékletű ideális gáz nyomásának (p) és térfogatának (V) szorzata állandó. A Melde-csőben lévő levegő megfelel ezeknek a feltételeknek, így a kísérlet során teljesül a pV szorzat állandósága.
Ha V1 jelöli a vízszintesen, V2 a nyitott véggel felfelé, V3 a nyitott véggel lefelé álló csőben a levegő térfogatát, akkor két-két állapotot összehasonlítva a Boyle-Mariotte törvény a következő módon írható fel:
(8.2)
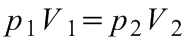, illetve:
.
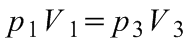A (8.1)-es egyenletek segítségével az előbbi összefüggések az alábbi alakba írhatók át:
(8.3)
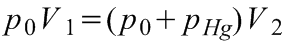, illetve:
,
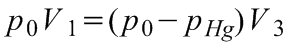ahonnan a külső légnyomás értéke két független méréssel is meghatározható:
(8.4)
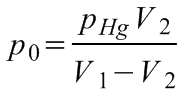, illetve:
.
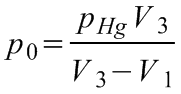Olvassa le a Melde-cső három helyzetében (vízszintes, két függőleges) a bezárt levegő térfogatát. Mivel a mérésnél a térfogatot tetszőleges egységben mérhetjük, vegyük az 1 mm hosszú csőrész térfogatát egységnyinek, így a térfogat meghatározásához elegendő a bezárt levegő hosszának a megadása. Ezután mérjük meg a higanyoszlop x hosszát is, ennek ismeretében a higanyoszlop hidrosztatikai nyomása számítható az alábbi formula alapján:
(8.5)
,
ahol g a nehézségi gyorsulást, ρ Hg a higany sűrűségét jelöli. g = 9,81 m/s2, ρ Hg = 13600 kg/m3. Mérési eredményeit foglalja az alábbi táblázatba.
8.1. táblázat - Táblázat a mérési eredményeknek.
|
x = ..................... m |
pHg = ....................... Pa |
|
p1 = p0 | |
|
V1 =......................te (te = térfogategység) | |
|
V2 = ....................... te |
V3 = ........................ te |
|
p0 = ...................... Pa |
p0 = ....................... Pa |
|
p0, átl = .................... Pa δrelatív = .... | |
A (8.4) egyenletek segítségével határozza meg a külső légnyomás értékeit, majd átlagolja azokat!
Számolja ki a légnyomás relatív eltérését a barométerről leolvasott, aktuális értéktől!
Hogyan befolyásolja a mérés pontosságát a Melde-csőben levő Hg-oszlop hosszúsága?
Számítsa ki a Boyle-Mariotte-féle törvényből a bezárt gáz nyomását a cső vízszintes és két függőleges helyzetében!
Milyen képletből számítható ki a higany hidrosztatikai nyomása?
Hogyan befolyásolja a Melde-csőben lévő higanyszál hossza a mérés pontosságát?
Definiálja a nyomást és SI mértékegységét!
Milyen kapcsolat van a következő nyomásegységek között: Hgmm, torr, Pa, mbar, atm?
Hogyan mérte meg Torricelli a légköri nyomást?
Melde-csövet úgy készíthetünk, hogy az üvegcsövet felmelegítjük, majd higanytálba tartjuk. Lehűlve higanyt szív fel a cső.
Melde francia származású egyetemi oktató volt.
A Melde-csővel való légnyomásmérés pontossága nem függ a higanyoszlop hosszától.
A légnyomás meghatározásához elegendő, ha a csövet vízszintes és egy függőleges állásban vizsgáljuk.
A hidrosztatika szó a hidrogén nevére utal, amely vízképzőt jelet.
Melde-cső segítségével, ismerve a légnyomás értékét a Boyle-Mariotte törvény is igazolható.
Tartalom
Kaloriméter és tartozékainak megismerése.
Az I. főtétel alkalmazása zárt rendszerre.
Hőkapacitás és fajlagos hőkapacitás kísérleti meghatározása.
Digitális mérleggel történő mérés gyakorlása.
Kaloriméter fedővel, belső hőmérővel és keverővel, külső hőmérő, digitális mérleg, főzőpoharak, mérőhenger, elektromos vízmelegítő, törlőkendő, víz, réz-próbatest.
9.1. ábra. A kaloriméter és a szükséges eszközök.
Dewar, Sir James (1842-1923) brit származású kémikus és fizikus, a Cambridge-i egyetem professzora volt. Spektroszkópiai kutatásai mellett jelentősek a gázok, elsősorban az oxigén és a hidrogén cseppfolyósítása területén elért eredményei. Ezen vizsgálataihoz kapcsolódva a cseppfolyós gázok tárolására alkotta meg a róla elnevezett vákuumköpenyes kialakítású ún. Dewar-edényt .
A kaloriméter kettős falú (kísérletünkben ételtermoszból kialakított) ún. Dewar-edény, amelynél a falak közötti tér légritkított, ezért jó hőszigetelő. A kaloriméterek folyadékok és szilárd testek fajhőjének, hőkapacitásának meghatározására, olvadáshő, forráshő, valamint hőmennyiség mérésére szolgáló kísérleti eszközök.
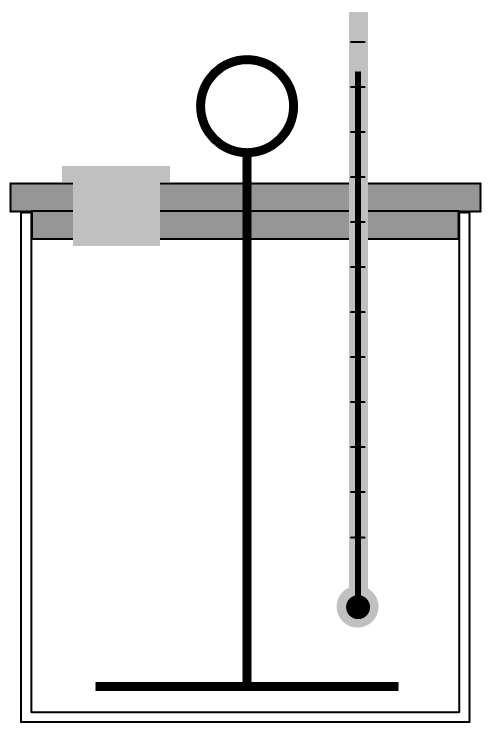
9.2. ábra. A kaloriméter és tartozékai.
A kaloriméter és tartozékai, a hőmérő és a keverő (lásd a 9.2. ábrát), a hőfelvétel- és leadás során szintén változtatják hőmérsékletüket, ezt befolyásolja a kaloriméter C hőkapacitása, amely számértékileg a kaloriméter egységnyi hőmérsékletváltozásához szükséges hőmennyiséggel adható meg:
(9.1)
.
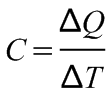A hőkapacitás egysége a J/K vagy J/°C. A testek hőkapacitása arányos a testek m tömegével és függ azok anyagi minőségétől (c):
(9.2)
.
A test anyagára jellemző, az egységnyi tömegű anyag hőmérsékletének egységnyi megváltoztatásához szükséges hőmennyiség, a fajhő vagy fajlagos hőkapacitás, amely az alábbi egyenlettel definiálható:
(9.3)
.
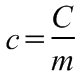A fajhő egysége: J/(kg K) vagy J/(kg °C). A fajhő ismeretében a termikus úton felvett vagy leadott hőmennyiség mértéke az alábbi összefüggéssel adható meg:
(9.4)
.
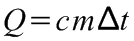A kaloriméter hőkapacitásának meghatározásához a kaloriméterbe ismert tömegű (m1) meleg vizet (fajhője: c) öntünk, majd néhány perc elteltével, a hőmérsékleti egyensúly beállta után leolvassuk a víz (és a kaloriméter) kezdeti hőmérsékletét (t1). Ezután ismert tömegű (m2) és ismert hőmérsékletű (t2) hideg vizet öntünk hozzá. Keverés és kis várakozás után újra leolvassuk a beálló közös hőmérsékletet (tk).
A mennyiségi leíráshoz alkalmazzuk a termodinamika első főtételét. Mivel a rendszer hőszigetelt (Q = 0) és mivel a folyadékoknál a térfogati munka elhanyagolható (W = 0), a belső energia változások előjeles összege zérussal egyenlő: Σ ΔEb = 0, azaz
(9.5)
.
Behelyettesítés után a szokásos termikus kölcsönhatást leíró egyenletet kapjuk:
(9.6)
.
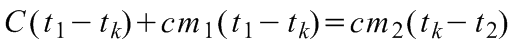Innen a kaloriméter hőkapacitása:
(9.7)
,
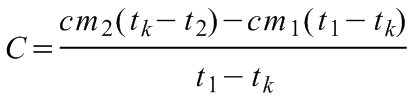ahol c a víz fajlagos hőkapacitása, 4180 J/(kg K).
A kalorimétereket szokás jellemezni a vízértékükkel is. A vízérték megmutatja, hogy a kaloriméter hőmérsékletének 1 °C-kal való megváltoztatásához szükséges hőmennyiség mekkora tömegű vizet melegítene fel 1 °C-kal:
(9.8)
.
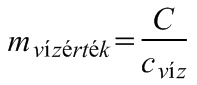Szilárd testek fajhőjének meghatározásánál a következőképpen kell eljárni. A most már ismert hőkapacitású kaloriméterbe lemért tömegű (m1) meleg vizet öntünk, majd kevergetés után, ha a hőmérséklet állandósult, leolvassuk a kaloriméter és a meleg víz kezdeti hőmérsékletét (t1). Ezután a bemért víztömeggel kb. egyenlő (m2) tömegű szilárd testet teszünk óvatosan a kaloriméterbe. Jól megkeverjük a vizet, és leolvassuk a beálló újabb közös hőmérsékletet (tk). A (9.1) és (9.2) egyenletek mintájára a belső energiák változására felírhatók az alábbi egyenletek:
(9.9)
,
(9.10)
,
ahonnan a szilárd test (réz) fajhője:
(9.11)
.
A gyakorlat során a meleg vízzel és az üveg eszközökkel óvatosan dolgozzon!
Mérési eredményeit foglalja az alábbi táblázatokba:
Határozza meg a kaloriméter hőkapacitását a (9.7) egyenlet alapján! Melegítsen 200 g tömegű vizet vízmelegítővel, kb. 80 °C-ra, majd öntse a kaloriméterbe! A hőmérséklet leolvasása után újabb 200 g tömegű, ezúttal szobahőmérsékletű vizet öntsön a kaloriméterbe! Olvassa le a közös hőmérsékletet! A víz tömegének meghatározását mérőhengerrel végzett térfogatmérésre vezetjük vissza: a V = 200 ml víz tömegét m = 200 g-nak tekinthetjük (ρvíz = 1000 kg/m3). A hőkapacitás meghatározását háromszor végezze el, számoljon átlagot!
Adja meg a kaloriméter vízértékét!
Határozza meg a kiadott réz próbatest fajlagos hőkapacitását (fajhőjét)! A próbatest tömegét digitális mérleggel mérje meg! Kb. ugyanekkora tömegű vízzel dolgozzon a feladatban. Mérését háromszor végezze el, számoljon átlagot!
A fajhőre kapott eredményt vesse össze az irodalomban található adattal! Számoljon relatív eltérést!
Elemezze a mérés hibaforrásait!
Mit értünk hőkapacitáson és fajhőn?
Milyen kapcsolat van egy test fajhője és hőkapacitása között?
Mit értünk a kaloriméter vízértékén?
A termodinamika I. főtételét alkalmazva vezesse le a kaloriméter hőkapacitására vonatkozó formulát!
A termodinamika I. főtételét alkalmazva vezesse le a szilárd test fajhőjére vonatkozó formulát!
Mi jellemzi a termodinamikai egyensúlyt?
A fajhő az egységnyi hőmérsékletre vonatkoztatott hőkapacitás.
A hőkapacitás mindig függ az anyag mennyiségétől / tömegétől / részecskeszámától.
A fajhő mértékegysége J/kg.
A hőmérsékleti egyensúly beállta a termodinamika II. főtételének teljesülését is jelzi.
A fajhő pontos meghatározásához a kaloriméter hőkapacitását is figyelembe kell venni.
A kaloriméter vízértékét úgy kapjuk meg, hogy a kaloriméter hőkapacitását elosztjuk a víz fajhőjével.
Tartalom
A jég és víz közötti termikus kölcsönhatás alapján a jég olvadáshőjének meghatározása.
Digitális mérleggel történő mérés gyakorlása.
Ha ismert C hőkapacitású kaloriméterben lévő m1 tömegű, t1 hőmérsékletű vízbe m2 tömegű, t2 hőmérsékletű jeget teszünk, a jég megolvad. Ha a beálló közös hőmérsékletet tk-val jelöljük, akkor a termikus kölcsönhatást leíró egyenlet:
(10.1)
,
ahonnan a jég olvadáshője meghatározható:
(10.2)
.
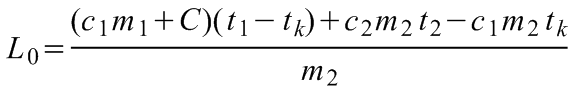L0 a jég olvadáshőjét, c1 a víz, c2 a jég fajhőjét jelöli.
Üres kaloriméterbe tegyen m1 tömegű vizet és olvassa le a kaloriméter hőmérőjéről a víz t1 hőmérsékletét. Ha a jeget a szokásos módon mérnénk le, akkor tömege csökkenne az olvadás és szublimáció miatt, ezért a következő módon kell eljárni. Digitális mérlegen tárázza ki a vízzel megtöltött kalorimétert tartozékaival együtt. A kiadott jégkockáról itassa le a vizet, és tegye a már száraz jeget a kaloriméterbe. Állandó kevergetés közben figyelje a kaloriméter hőmérőjét és olvassa le az elért legalacsonyabb hőmérsékletet. Ezt a hőmérséklet tekintjük közös hőmérsékletnek (tk). A kalorimétert helyezze újra a mérlegre, a mutatott érték lesz a jég m2 tömege.
A jég minél előbb kerüljön a hűtőszekrényből a kaloriméterbe, mert így a jég t2 hőmérsékletéül a hűtőszekrényben mért hőmérsékletet fogadhatjuk el.
A mért adatok ismeretében a (10.2) egyenlet segítségével határozza meg a jég olvadáshőjét! Végezze el a mérést háromszor! Adatait foglalja táblázatba!
Adja meg a kapott olvadáshő irodalmi értéktől való százalékos eltérését (δrel)!
Elemezze a mérés hibaforrásait!
Definiálja az olvadáshőt és adja meg az SI mértékegységét!
A termodinamika I. főtételét alkalmazva vezesse le a jég olvadáshőjére vonatkozó formulát!
Milyen hibaforrási vannak a mérésnek?
Számolja ki a jég olvadáshőjét az alábbi adatokból: A kaloriméterben 655 g víz van, hőmérséklete 35,7 °C. A kaloriméter hőkapacitása 100 J/°C. A kaloriméterbe 86 g, -18 °C hőmérsékletű jeget teszünk. A beálló közös hőmérséklet 21,8 °C. A víz fajhője 4180 J/(kg °C), a jég fajhője 2090 J/(kg °C).
Milyen kialakítású a keverési kaloriméter (Dewar-edény) és miért?
Mi jellemzi a termodinamikai egyensúlyt?
A jég olvadáshője 2,256ˇ106 J/kg.
Az olvadáshő felszabaduló hőmennyiség.
A jég olvadáshője megegyezik a víz fagyáshőjével.
Az olvadáshő megmutatja, hogy milyen erős a kötés a még szilárd test részecskéi között.
A kísérletekben a jég kezdeti hőmérséklete értékéül a hűtőszekrény mélyhűtőjének hőmérsékletét fogadhatjuk el.
A jég olvadáshőjének extrém nagy értéke is befolyásolja az óceáni hőmérsékletet.
Tartalom
Mikroszkóp felépítésének megismerése.
Okulárskála hitelesítése.
Tárgymikrométer és szerepének megismerése.
Mikroszkóp felhasználása hosszúságmérésre.
Mikroszkóp három objektívvel, okulárskála, fémszál-, hajszál- preparátum, biológiai minta, optikai rács, vonalzó.
11.1. ábra. Mikroszkóp.
A mikroszkóp lényegében két gyűjtőlencséből áll, amelyeket sematikusan egy-egy lencsével helyettesíthetünk (11.2. ábra). A T tárgyról az objektív nagyított, valódi és fordított állású, ún. közbülső képet (K) ad, amelyet az okulárral, azaz egy lupéval tovább nagyítunk. Ha az okulárt úgy helyezzük el, hogy az objektív által előállított valódi kép az okulár fókuszsíkjában keletkezzen, akkor a végső kép virtuális, a tárgyhoz viszonyítva fordított állású, erősen nagyított lesz. Az objektív és az okulár egymás felé eső fókuszpontjainak távolságát optikai tubushossznak (Δ) nevezzük, szokásos értéke 160 mm.
11.2. ábra. Sugármenet a mikroszkópban.
A mikroszkóppal való hosszmérések célját szolgálja az ún. okulár-mikrométer. Az okulár-mikrométer üveglemezre karcolt ismert (pl. 0,1 mm vagy 0,05 mm) vagy ismeretlen beosztású skála, amelyet a valódi kép keletkezésének helyén, a tubusban helyeznek el. Így az okulárral egyszerre látjuk élesen a tárgy mikroszkópi képét és az okulár-mikrométer skáláját.
Ha az okulárskála ismeretlen beosztású, akkor hitelesíteni kell egy ún. tárgymikrométer segítségével. Ilyenkor a mikroszkópot úgy állítsuk be, hogy a mikroszkópon át egyszerre lássuk élesen a tárgyasztalra helyezett tárgymikrométer hiteles osztásait és az okulárskála skálarészeit. A megfelelő aránypárból az okulárskála beosztása meghatározható (mm/skálarész). Ezt a hitelesítést minden objektívnél el kell végezni.
A hitelesítés után válik alkalmassá a mikroszkóp hosszmérésre. Ilyenkor megkeressük a mérendő tárgy éles képét a mikroszkóp legmegfelelőbb nagyítású objektívjével, majd leolvassuk, hogy hány okulárskála beosztás a mérete, és ezt a skálabeosztás számot megszorozzuk a hitelesítési értékkel.
A mikroszkóp nagyítását a megfelelő lencsék nagyításainak szorzata adja:
(11.1)
,
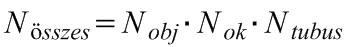ahol Nobj az objektív nagyítása, Nok az okulárlencse nagyítása, Ntubus a tubuslencse nagyítása.
Hitelesítse a mikroszkóp okulárskáláját 10-szeres nagyítású objektívét és 10-szeres nagyítású okulárját használva! A hitelesítéshez használja a tárgymikrométert!
Az előző okulárt és objektívet használva mérje meg a kiadott hajszálak és optikai szál vastagságát!
Hitelesítse a mikroszkóp okulárskáláját 10-szeres nagyítású objektívét és 5-szörös nagyítású okulárját használva! A hitelesítéshez használja a tárgymikrométert!
Az utóbbi okulárt és objektívet használva mérje meg a kiadott hajszálak és optikai szál vastagságát!
Vizsgálja, nézze meg a kiadott biológiai mintákat! Jegyezze fel, mekkora össznagyítást alkalmazott a mikroszkópban!
Képalkotásnál milyen típusú képek jöhetnek létre, és mi a jellemzőjük?
A nevezetes sugarakon alapuló képszerkesztéssel értelmezze a mikroszkóp működését, készítsen ábrát!
Milyen típusú végső képet alkot a mikroszkóp? Válaszát magyarázza meg!
Mit nevezünk tárgymikrométernek és mire használjuk?
Ismertesse az okulár skála hitelesítésének lépéseit!
Hogyan méri meg a kiadott tárgyak lineáris méretét?
Ahhoz, hogy a mikroszkópot hosszúságmérésre használhassuk, az okulárskáláját hitelesíteni kell.
A tárgymikrométer üveglemezre karcolt beosztás. Általában 50 vagy 100 osztás van 1 mm-en.
A tárgymikrométert a tubusban kell elhelyezni.
A mikroszkóp össznagyítása nem függ a tubuslencse nagyításától.
A nagyítás növelésével a mikroszkópi kép egyre világosabb lesz.
A mikroszkóp szemhez közeli lencséjét okulárnak, a tárgyhoz közeli lencséjét objektívnek nevezzük.
Tartalom
Az optikai képalkotás vizsgálata.
A leképezési törvény használata.
Grafikus ábrázolás gyakorlása.
Pasco gyártmányú optikai sín cm-es beosztással, fényforrással (megvilágított célkereszt), ernyővel, 10 cm és 20 cm névleges fókusztávolságú műanyaglencsék az optikai sínre illeszkedő speciális foglalatban.
12.1. ábra. Az optikai sín és tartozékai.
A gyűjtőlencse a ráeső párhuzamos sugarakat a lencse másik oldalán közel egyetlen pontba, a fókuszpontba gyűjti össze. A fókuszpont távolsága a lencse középpontjától a lencse jellemző paramétere, a fókusztávolság (f). Ennek meghatározására több módszer is létezik. Az egyik lehetőség a vékonylencsékre érvényes leképezési törvény alkalmazása, amely mennyiségi összefüggést ad a tárgytávolság (t), a képtávolság (k) és a fókusztávolság között:
(12.1)
.
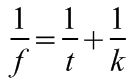A méterekben kifejezett fókusztávolság reciprok értékét dioptriának (D), vagy törőerősségnek nevezzük. Minél nagyobb a dioptria értéke, annál jobban megtöri a lencse a rajta áthaladó fényt.
(12.2)
.
A lencse fókusztávolsága és dioptriája meghatározható az optikai padon végzett leképezési kísérletsorozat alapján, a tárgytávolság és a képtávolság mérésével.
A 12.2. ábrán vázolt elrendezés alapján különböző tárgytávolságokat választva az ernyő mozgatásával keresse meg azt a helyet, ahol a tárgyként használt célkereszt képe (lásd a 12.2. ábrát) élesen látszódik az ernyőn. A kép lehet kicsinyített és nagyított is. Olvassa le az optikai sínre rögzített skálán az összetartozó tárgy- és képtávolságokat.
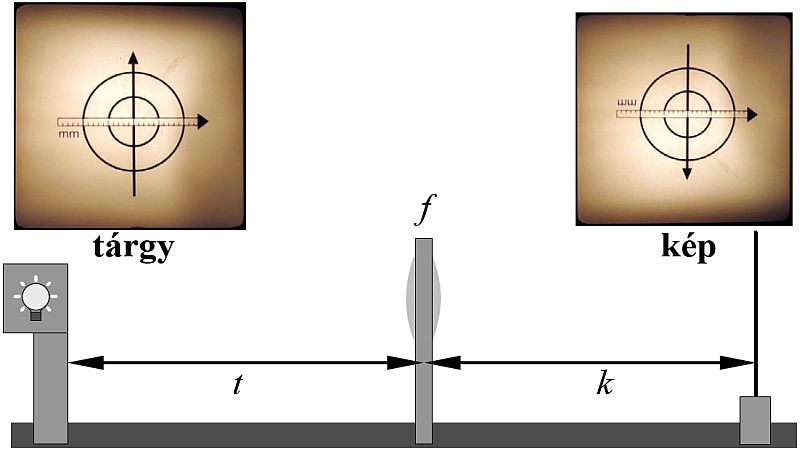
12.2. ábra. Optikai elrendezés a fókusztávolság meghatározásához fényforrással, lencsével, ernyővel.
A (12.1) összefüggés alapján számítsa ki a fókusztávolságokat. Eredményeit foglalja az alábbi táblázatokba.
Későbbi tanulmányai során meg fog ismerkedni más fókusztávolság meghatározási módszerekkel, így a Bessel- és Abbe-módszerrel is, amely módszerek vastag lencsék fókusztávolságának meghatározására is alkalmasak.
Tanulmányozza az összeállított kísérleti berendezést!
Becsülje meg a kiadott lencsék fókusztávolságát!
Határozza meg a 10 cm-es névleges fókusztávolságú lencse fókusztávolságát öt mérésből! Számoljon szórást, átlagot és relatív eltérést! Az eredményeket foglalja táblázatba!
Határozza meg a 20 cm-es névleges fókusztávolságú lencse fókusztávolságát öt mérésből! Számoljon szórást, átlagot és relatív eltérést! Az eredményeket foglalja táblázatba!
Ábrázolja mindegyik méréssorozatnál az 1/k értékek függvényében az 1/t értékeket! A kapott egyenes tengelymetszeteiből is határozza meg a fókusztávolság értékét!
Adja meg a lencsék dioptriájának értékeit!
Mit értünk fókusztávolság alatt, és hogyan becsülhető meg a gyűjtő lencse esetén?
Írja fel a lencsék leképezési törvényét! Mi a dioptria?
Mi a nagyítás definíciója, és hogyan számítható ki a tárgy- és képtávolságból?
Hogyan számítható ki egy vékony gömbi lencse fókusztávolsága? Mikor működik egy lencse gyűjtő vagy szóró lencseként?
Hogyan határozta meg grafikus úton a lencsék fókusztávolságát? Válaszát indokolja!
Ismertesse az Abbe- és a Bessel-féle fókusztávolság meghatározási módszer lényegét, és írja fel a megfelelő formulákat!
Vékonylencsék fókusztávolsága a fókuszpont és a lencse távolsága.
Vékonylencsék fókusztávolsága nem függ a lencse anyagának környezetre vonatkozó törésmutatójától.
Sík-domború lencse egyik görbületi sugara nulla.
Éles képet csak akkor kaphatunk, ha az ernyő és a tárgy távolsága a fókusztávolság négyszeresénél nagyobb.
Domború lencse fókusztávolsága mindig pozitív.
Domború lencse elé az egyszeres és kétszeres fókusztávolság közé helyezve a tárgyat mindig nagyított, látszólagos képet kapunk. Ez az egyszerű nagyító leképezése.
Tartalom
Optikai Hartl-korong megismerése.
A fényvisszaverődés és fénytörés törvényeinek igazolása.
Törésmutató-meghatározás.
Hartl-korong és tartozékai, lézer, üvegbot, fémállvány, tolómérő.
13.1. ábra. Hartl-korong és tartozékai.
Az első optikai korongot, amelyet a fényvisszaverődés és fénytörés jelenségeinek demonstrálására és mérésére fejlesztettek ki, a Max Kohl tanszerkatalógus említi 1900-ból. Az általunk is használt elrendezésű optikai korong, a Hartl-korong tervezője Hans Hartl osztrák professzor volt. Ezt a típusú eszközt a Central Scientific katalógus említi először 1928-ban.
Ha fény esik valamely optikailag átlátszó test vagy közeg határfelületére, a határfelületről a fény egy része visszaverődik, másik része behatol a közegbe.
A fényvisszaverődés törvénye kimondja, hogy a beeső fénysugár, a beesési merőleges és a visszavert fénysugár egy síkban van, valamint, hogy az α' visszaverődési szög egyenlő az α beesési szöggel.
A fénytörés törvénye (Snellius-Descartes törvény) kimondja, hogy a beeső fénysugár, a beesési merőleges és a megtört fénysugár egy síkban van, valamint az α beesési és a β törési szög szinuszainak hányadosa a beesési szögtől független, a két közegre jellemző állandó, a második közegnek az elsőre vonatkoztatott relatív törésmutatója, jelölése: n21.
(13.1)
.
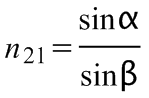A relatív törésmutató megegyezik a két közeg vákuumra (levegőre) vonatkozó ún. abszolút törésmutatóinak hányadosával.
(13.2)
.
Teljes visszaverődés: Ha optikailag sűrűbb közegből optikailag ritkább közeg felé halad a fény, azaz ha n21 < 1, akkor bizonyos beesési szöghöz, az ún. határszöghöz 90°-os törési szög tartozik. Amennyiben a határszögnél nagyobb beesési szögben érkezik a fény a határfelületre, akkor nem jut át a második közegbe, hanem teljesen visszaverődik a visszaverődés törvényeinek megfelelően. A 13.2. egyenlet alapján egyszerűen belátható, hogy a két közeg abszolút törésmutatója határozza meg a határszöget.
(13.3)
.
13.2. ábra. A beeső és a megtört fény sugármenete.
Fénytörés planparalel-lemezen: A két párhuzamos síkkal határolt átlátszó lemezre ferdén beeső fénysugár a belépésnél és a kilépésnél is megtörik. Ha a lemez mindkét oldalán ugyanaz a közeg van, akkor a lemezből kilépő fénysugár a belépőhöz képest párhuzamosan eltolódik (lásd a 13.3. ábrát).
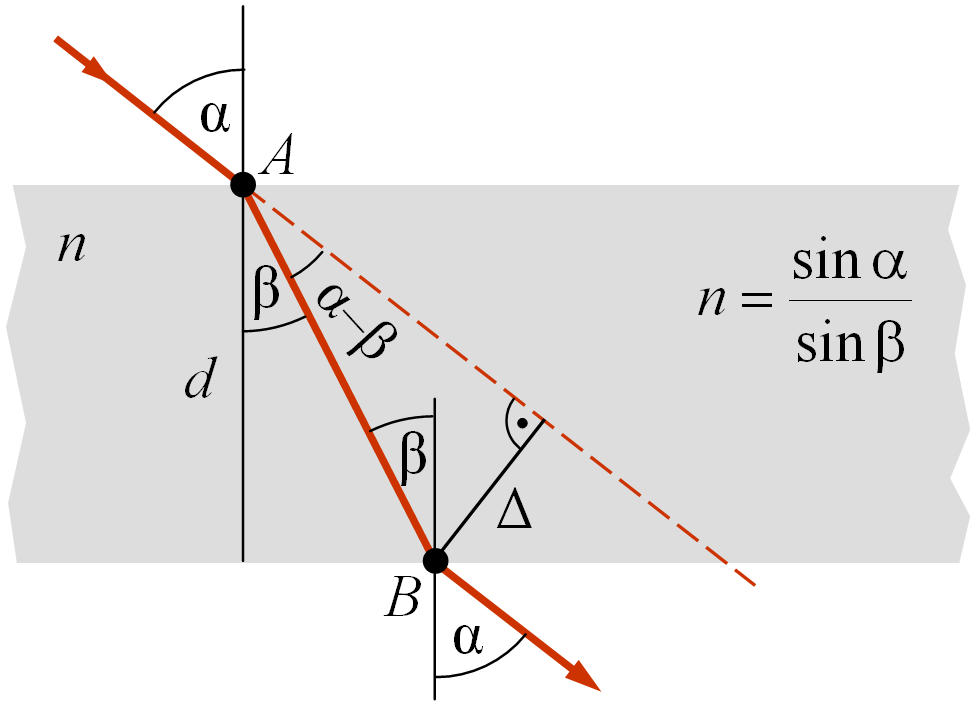
13.3. ábra. Fénytörés planparalel-lemezen.
Az eltolódás mértéke függ a beesés szögétől (α), a planparalel-lemez törésmutatójától (n) és a lemez vastagságától (d). A törés törvényének alkalmazásával és egyszerű trigonometriai megfontolásokkal belátható, hogy az eltolódás (Δ) nagysága az alábbi összefüggéssel adható meg:
(13.4)
.
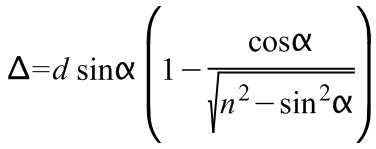Hélium-neon lézer fénysugarát egy üvegbot segítségével kicsit szétterítjük, majd ráirányítjuk a Hartl-korongra rögzített optikai eszközre (mely lehet tükör, lencse, planparalel-lemez, stb). A törés törvényének kvantitatív vizsgálatánál speciális félkör keresztmetszetű testet (félhengert) használunk.
A Hartl-korong forgatható, peremén szögosztással ellátott, ezért kényelmesen be tudjuk állítani a különböző beesési szögeket, és könnyen leolvashatjuk a speciális félkör alak miatt a második határfelületen irányváltoztatás nélkül haladó fénysugár törési szögét. A korong peremén található szögosztás a szögek leolvasását fok pontossággal biztosítja, ha kell, a fél fokot becsüljük meg. A mérési adatokat foglalja az alábbi táblázatokba.
A lézerfénnyel óvatosan dolgozzon, a gyakorlat során fokozottan ügyeljen arra, hogy sem a direkt, sem a reflektálódott lézerfény ne kerüljön saját és társai szemébe!
Igazolja a visszaverődés törvényét! Helyezzen síktükröt a Hartl-korongra, állítson be különböző beesési szögeket, és olvassa le a visszaverődési szögeket!
Igazolja a törésre vonatkozó Snellius-Descartes törvényt! Helyezze fel a Hartl-korongra a félkör keresztmetszetű testet! Állítson be 10, 20, 30, 40, 50, 60, 70, 80°-os beesési szöget, és olvassa le a hozzá tartozó törési szögeket! Az adatokból számolja ki a műanyag test levegőre vonatkozó relatív törésmutatóját!
Mérje meg a teljes visszaverődés határszögét a Hartl-korongra helyezett félkör alakú test segítségével! A határszögből is határozza meg a törésmutató értékét!
Mérje meg a Hartl-korongra helyezett planparalel-lemezen az eltolódás mértékét különböző beesési szögeknél! Ennek felhasználásával számolja ki a planparalel-lemez törésmutatóját a (13.4) formula alapján! A planparalel-lemez vastagságát tolómérővel mérje meg!
A használt optikai elemek anyaga azonos. Ennek tudatában vesse össze a kapott törésmutatókat! Elemezze az eljárásokat a mérési pontosság szempontjából!
Fogalmazza meg a szabályos fényvisszaverődés törvényeit, és hogyan igazolta ezeket!
Fogalmazza meg a fénytörés törvényeit, és hogyan igazolta ezeket!
Mikor jön létre a teljes visszaverődés jelensége?
Mi a határszög, és milyen optikai elemmel mérte meg azt?
Hogyan halad át egy fénysugár egy planparalel-lemezen, és milyen hatása van ennek a testek látszólagos helyére vonatkozólag? Válaszát részletesen indokolja!
Mi az optikai szál és hogyan működik?
A Hartl-korong lehet függőleges és vízszintes síkú elrendezésű is.
A Hartl-korongot már a középkorban is ismerték.
A fényvisszaverődés törvénye Snellius és Descartes nevéhez fűződik.
A teljes visszaverődés jelensége valójában a fénytörés egy speciális esete.
Két közeg relatív törésmutatója a két közeg vákuumra vonatkozó relatív törésmutatóinak a hányadosa.
A vákuumra vonatkozó relatív törésmutató az abszolút törésmutató.
Tartalom
Elektromos áramköri elemek megismerése, elektromos kapcsolások összeállításának gyakorlása.
Áramerősséget, feszültséget, ellenállást mérő alapműszerek megismerése, használata.
Mérőműszerek méréshatárának megismerése.
Mérőműszerek leolvasásának gyakorlása.
9 db különböző ellenállást tartalmazó áramköri panel, 12 V-ig változtatható, 2 A-ig terhelhető egyenfeszültségű feszültségforrás, 2 db digitális multiméter, vezetékek.
14.1. ábra. Az ellenállásokat tartalmazó panel elő- és hátlapja és a szükséges eszközök.
A feszültség és áramerősség közötti egyenes arányosságot Georg Simon Ohm (1787-1854) német fizikus és matematikus állapította meg 1827-ben, ezért tiszteletére róla nevezték el a törvényt és az ellenállás mértékegységét is: 1 ohm = 1 Ω = 1 V/A. Ohm az elektromosságtan mellett foglalkozott kristályoptikával, a hangtanban ő alkalmazta először a Fourier-analízist.
Ohm-törvénye kimondja, hogy egy homogén, állandó keresztmetszetű, áramjárta vezető két pontja között mért potenciálkülönbség, feszültség (U) egyenesen arányos az átfolyó áram erősségével (I). A két mennyiség hányadosa állandó, a vizsgált vezetőszakaszra jellemző, ez az elektromos ellenállás (R):
(14.1)
.
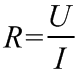Az ellenállás, a feszültségforrás, az áramerősségmérő műszer, és a feszültségmérő műszer rajzjelei, amelyet elektromos kapcsolásokban használunk a 14.2. ábrán láthatók. Ellenállás (fogyasztó): R, feszültségforrás: U, áramerősségmérő műszer: A, feszültségmérő műszer: V
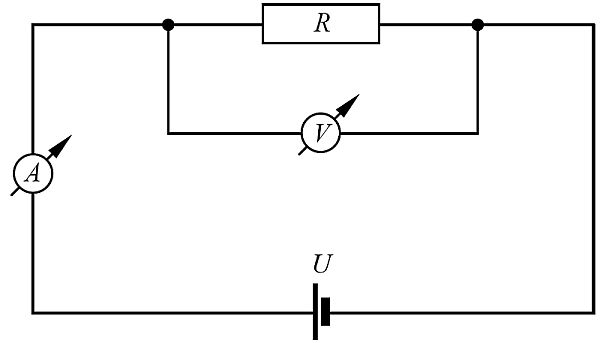
14.2. ábra. Az ellenállás-méréshez szükséges kapcsolási rajz.
Ezeket az áramköri elemeket az áramkörben vezeték köti össze (gyakorlatban röpzsinórnak is nevezzük). Mivel az áramköröknél használt vezetékek saját ellenállása a fogyasztók ellenállásához viszonyítva elhanyagolható, ezért azt megállapodás szerint zérusnak tekintjük.
Az áramerősségmérő műszert sorosan kapcsoljuk az áramkörbe, mert az áram átfolyik rajta. Az ideális ampermérő elhanyagolható belső ellenállással rendelkezik, így elhanyagolható a rajta eső feszültség is.
A feszültségmérő műszert párhuzamosan kell csatlakoztatni ahhoz a fogyasztóhoz, amin a feszültséget mérjük. Az ideális voltmérő belső ellenállása végtelenül nagy, így az áramkörben folyó áram erősségét nem változtatja meg.
Ha az ún. kombinált mérőműszert ellenállásmérésre használjuk, (ohm-mérő) akkor egy, a mérőműszer dobozába épített feszültségforrást kapcsolunk az áramkörbe, és tulajdonképpen az Ohm-törvény alapján határozzuk meg az ellenállást úgy - ez a mutatós, ún. analóg műszernél jól is látható, - hogy egy hitelesített skáláról leolvassuk az ellenállás értékét.
Az általunk is használt számkijelzéses, ún. digitális műszerrel mérni lehet áramerősséget, feszültséget és ellenállást, egyenáramú és váltakozó áramú üzemmódban egyaránt. A műszer forgatógombjával lehet kiválasztani a mérni kívánt mennyiségeket. A műszeren öt csatlakozó pont található. Ezek közül egyik, a COM feliratú a földelt, és mindhárom mérési üzemmódban ez a negatív pólus. A másik négyből (mA, A, V, Ω) értelemszerűen, felirat szerint kell kiválasztani a másik pólust.
Állítsa össze a 14.2. ábrán látható kapcsolást!
Határozza meg feszültség- és áramerősség-méréssel az Ohm-törvény alapján a kiadott ellenálláspanel 1, 2, 3, 4, stb jelű ellenállásainak értékét! Adott ellenállást három különböző feszültségértéknél határozzon meg!
Mérje meg a kiadott ellenállások értékét ohm-mérővel!
Mérési eredményeit foglalja táblázatba!
Számolja ki az Rszámolt és Rmért értékek relatív eltérését (δrelatív)!
Fogalmazza meg Ohm törvényét!
Hogyan kapcsolja az áramkörbe az ampermérőt és a voltmérőt?
Milyen belső ellenállású az ideális ampermérő és voltmérő? Miért?
Hogyan függ egy vezető ellenállása a geometriai és fizikai adataitól?
Hogyan határozta meg a kiadott ellenállások értékét, és hogyan ellenőrizte méréseinek helyességét?
Mi a Joule-féle hő és hogyan jön létre?
A fémek ellenállása egyenesen arányos a vezető keresztmetszetével és fordítottan arányos a hosszával.
A fémek ellenállása nem függ a vezető hőmérsékletétől.
A róla elnevezett törvényt Ohm német matematikus és fizikus állította fel 1727-ben.
Az egyszerű áramkör részei: áramforrás, fogyasztó, kapcsoló, áramerősségmérő műszer, feszültségmérő műszer.
Az ellenállásmérő műszer beépített feszültségforrást használ az ellenállásméréshez.
A fajlagos ellenállás értékeinek ismeretében eldönthető azonos hosszúságú, különböző anyagból készült vezetők ellenállásának egymáshoz való viszonya.
Tartalom
Sorosan és párhuzamosan kapcsolt ellenállásokra vonatkozó összefüggések igazolása.
Elektromos áramköri elemek megismerése, kapcsolások összeállításának gyakorlása.
3-3 db ellenállást soros, illetve párhuzamos kapcsolásban tartalmazó áramköri panel, 12 V-ig változtatható, 2 A-ig terhelhető egyenfeszültségű feszültségforrás, 2 db digitális multiméter, vezetékek.
15.1. ábra. Sorosan és párhuzamosan kapcsolt ellenállások és a szükséges eszközök.
A 15.2. ábrán látható ellenállások soros kapcsolásúak, ennek következményeként az áramköri elemeken azonos értékű áram folyik át. Az egyes ellenállásokon eső feszültségek összege egyenlő az áramforrás kapocsfeszültségével.
(15.1)
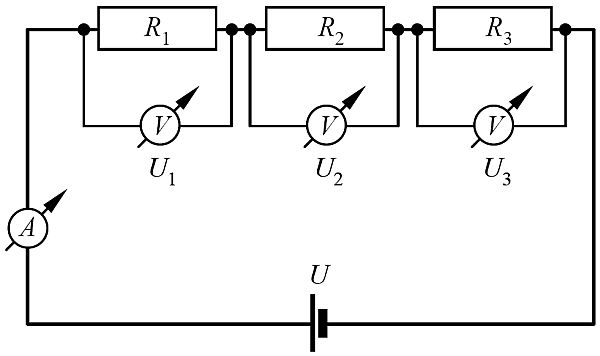
15.2. ábra. Ellenállások soros kapcsolása.
A kapocsfeszültség, illetve az egyes ellenállásokon mérhető feszültség és az átfolyó áram erőssége között érvényes az Ohm-törvény:
(15.2)
.
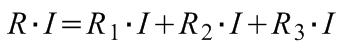A (15.2) egyenlet egyszerűsítésével adódik a sorosan kapcsolt ellenállások eredőjére vonatkozó összefüggés, amely szerint sorba kapcsolt ellenállások eredője megegyezik az egyes ellenállások összegével:
(15.3)
.
A 15.3. ábrán látható ellenállások párhuzamos kapcsolásúak, az ellenállásokon eső feszültség így azonos. Az ellenállásokon átfolyó áramok összege a csomóponti Kirchhoff-törvény miatt - ami a töltésmegmaradás következménye - megegyezik a főáramköri áramerősséggel:
(15.4)
.
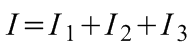15.3. ábra. Ellenállások párhuzamos kapcsolása.
Alkalmazva Ohm-törvényét az egyes ellenállásokon eső feszültségek és a rajtuk átfolyó áramerősségek között:
(15.5)
.
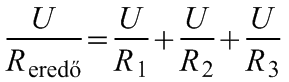A (15.5) egyenlet egyszerűsítéséből adódik a párhuzamosan kapcsolt ellenállások eredőjére vonatkozó összefüggés:
(15.6)
,
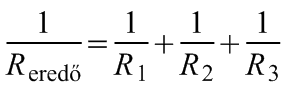amely szerint az ellenállások eredőjének reciproka megegyezik az egyes ellenállások reciprokainak összegével.
Állítsa össze a 15.2. ábrán látható kapcsolást! Igazolja a sorosan kapcsolt ellenállások eredőjére vonatkozó (15.3) összefüggést!
Igazolja, hogy az egyes ellenállásokon eső feszültségek aránya megegyezik az ellenállások arányával!
Határozza meg Reredő értékét úgy is, hogy U értékét közvetlenül méri meg! Magyarázza meg Reredő és (Reredő)' értékének különbözőségét!
Változtassa meg az áramforrás kapocsfeszültségét, majd ismételje meg a mérést! Eredményeit foglalja újabb táblázatba!
Állítsa össze a 15.3. ábrán látható kapcsolást! Igazolja a párhuzamosan kapcsolt ellenállások eredőjére vonatkozó (15.6) összefüggést!
Igazolja, hogy a párhuzamos ágakban folyó áramok erősségei a megfelelő ellenállásokkal fordítottan arányosak!
Határozza meg Reredő értékét úgy is, hogy I értékét közvetlenül méri meg! Magyarázza meg Reredő és (Reredő)' értékének különbözőségét!
Mérési eredményeit foglalja a megfelelő táblázatba!
Mit ért soros kapcsoláson, és hogyan számítható ki az eredő ellenállás?
Mit ért párhuzamos kapcsoláson, és hogyan számítható ki az eredő ellenállás?
Fogalmazza meg Kirchhof csomópont- és huroktörvényét!
Kirchhoff-féle csomópont- és huroktörvényt alkalmazva vezesse le a soros és párhuzamos kapcsolás eredő ellenállására vonatkozó formulákat!
Mi a Wheatstone-féle hidas ellenállásmérés lényege?
Hogyan változik a fémek és félvezetők ellenállása a hőmérséklet függvényében és miért?
Az ideális áramerősségmérő műszer azért kis ellenállású, hogy rajta kevés áram folyjon át.
Az ideális feszültségmérő azért nagy ellenállású, hogy rajta és a vele párhuzamosan kapcsolt fogyasztón nagy feszültség essen.
Párhuzamosan kapcsolt ellenállások eredőjének levezetésekor a csomóponti törvényt kell felhasználni.
Kircchoff csomoponttörvénye törvénye a töltésmegmaradást fejezi ki.
Párhuzamosan kapcsolt ellenállások eredője kisebb lesz bármelyik ellenállásnál.
Sorosan kapcsolt ellenállásoknál a telep belső ellenállása nem befolyásolja a kialakuló áramerősséget.
I. Zárthelyi dolgozat
Egyenes vonalú egyenletes mozgás vizsgálata Mikola-csővel. Hogyan függ a buborék sebessége a cső hajlásszögétől? Milyen grafikont kapott? (5 pont)
A dinamika alapegyenletének vizsgálata Atwood-féle ejtőgéppel. Hogyan igazolta a dinamika alapegyenletének helyességét az Atwood-féle ejtőgéppel? Rajzolja fela kísérleti elrendezést, jelölje az erőket! Vezesse le a felhasznált összefüggést! (10 pont)
A nehézségi gyorsulás meghatározása matematikai ingával. Mely mennyiségek felhasználásával és hogyan határozható meg grafikusan a nehézségi gyorsulás értéke? (5 pont)
Tehetetlenségi nyomaték meghatározása fizikai inga lengésidejének mérésével. Adja meg a fizikai inga lengésidejére vonatkozó összefüggést. Nevezze meg a benne szereplő fizikai mennyiségeket! (5 pont)
Egyenletesen gyorsuló forgómozgás dinamikai vizsgálata. a) Írja fel a forgómozgás alapegyenletét! Nevezze meg a benne szereplő fizikai mennyiségeket! b) Definiálja a tehetetlenségi nyomatékot! (2+2 pont)
Jég olvadáshőjének meghatározása keverési kaloriméterrel. Számolja ki a jég olvadáshőjét az alábbi adatokból! A kaloriméterben 655 g víz van, hőmérséklete 35,7 °C. A kaloriméter hőkapacitása 100 J/°C. A kaloriméterbe 86 g, -18 °C hőmérsékletű jeget teszünk. A beálló közös hőmérséklet 21,8 °C. A víz fajhője 4180 J/(kgˇ°C), a jég fajhője 2090 J/(kgˇ°C). (5 pont)
Mérések Melde-csővel. a) Vezesse le a légnyomás meghatározására használt összefüggéseket. b) Váltsa át a légnyomás 105 Pa értékét bar-ra. (4+1 pont)
Fókusztávolság meghatározása távolságtörvény alapján. Hogyan határozta meg grafikus úton a lencsék fókusztávolságát. Válaszát indokolja! (5 pont)
Optikai mérések Hartl-koronggal. a ) Mikor jön létre a teljes visszaverődés jelensége? b) Hogyan, milyen optikai elemmel mérte ki a törés törvényét? (2+3 pont)
Ohm-törvény vizsgálata, illetve Ellenállások soros és párhuzamos kapcsolása. Hogyan kapcsolja az áramkörbe az ampermérőt és a voltmérőt? Milyen belső ellenállású az ideális ampermérő és voltmérő? Miért? (4 pont)
Általános kérdések. a) Foglalja össze a grafikonkészítés szabályait! b) Hogyan számol relatív eltérést? c) Definiálja a szórást! (5+1+1 pont)
Értékelés
51%-62% (elégséges), 63%-74% (közepes), 75%-86% (jó), 87%-100% (jeles).
II. Zárthelyi dolgozat
Egyenes vonalú egyenletes mozgás vizsgálata Mikola-csővel. Hogyan igazolta a buborék egyenletes mozgását? (5 pont)
Egyenes vonalú egyenletesen gyorsuló mozgás vizsgálata lejtőn. Mely mennyiségek felhasználásával és hogyan határozta meg grafikus úton a lejtőn leguruló golyó gyorsulását? (5 pont)
A dinamika alapegyenletének vizsgálata Atwood-féle ejtőgéppel. Rajzolja le a kísérleti elrendezést, írja fel a mozgásegyenleteket! (5 pont)
A nehézségi gyorsulás meghatározása matematikai ingával. Hogyan határozható meg a nehézségi gyorsulás értéke? (5 pont)
Tehetetlenségi nyomaték meghatározása fizikai inga lengésidejének mérésével. Írja fel a fizikai inga mozgását leíró mozgásegyenletet! Nevezze meg a benne szereplő fizikai mennyiségeket! (5 pont)
Ideális gáz állapotegyenletének kísérleti igazolása. a) Fogalmazza meg az ideális gázokra vonatkozó állapotegyenletet, nevezze meg a benne szereplő mennyiségeket. b) Hogyan határozta meg a kísérletben a bezárt levegő mennyiségét (mólszám és részecskeszám) (3+5 pont)
Mérések Melde-csővel. a) Hogyan számol hidrosztatikai nyomást (formula, mennyiségek)? b ) Milyen kapcsolat van a Hgmm és a torr, továbbá a Pa és a mbar nyomásegységek között? (5+1+1 pont)
Fókusztávolság meghatározása távolságtörvény alapján. Hogyan becsülte meg a lencsék fókusztávolságát? Válaszát indokolja! (5 pont)
Optikai mérések Hartl-koronggal. a) Fogalmazza meg a Snellius-Descartes törvényt! b) Hogyan, milyen optikai elemmel mérte meg a határszöget? Készítsen rajzot!(3+2 pont)
Ohm-törvény vizsgálata, illetve Ellenállások soros és párhuzamos kapcsolása. a) Fogalmazza meg Ohm törvényét! b ) Készítsen kapcsolási rajzot ellenállásméréshez! c) Készítsen kapcsolási rajzot ellenállások soros és párhuzamos kapcsolása esetén az eredő ellenállás meghatározásához! Milyen mennyiségeket mért, hogyan számolt? (2+2+6 pont)
Általános kérdések. a) Hogyan számol meredekséget, mi a "haszna"? b) Hogyan számol relatív eltérést? c) Definiálja a szórást! (3+1+1 pont)
Értékelés
51%-62% (elégséges), 63%-74% (közepes), 75%-86% (jó), 87%-100% (jeles).