Tartalom
- Előszó
- 1. Az ultrarövid fényimpulzusok tulajdonságai
- 2. A rövid fényimpulzusok leírása
- 3. Impulzushossz és spektrális sávszélesség, határozatlansági reláció
- 4. Az ultrarövid lézerimpulzusok terjedése diszperzív közegben
- 5. Optikai elemek diszperziós tulajdonságai
- 6. Szögdiszperzió és hatásai
- 7. Impulzusok időbeli alakjának formálása, impulzuskompresszió
- 8. Szélessávú fényjelek fókuszálása
- 9. Optikai aberrációk és impulzusfronttorzulás
- 10. Optikai elemek spektrális fázisfüggvényének mérése
- 11. A szögdiszperzió mérése
- 12. Az ultrarövid impulzusok időbeli alakjának mérési módszerei
A bennünket körülvevő reális világ fizikai, biológiai és kémiai elemi folyamatainak nagy része femto- illetve attoszekundumos időskálán játszódik le. Az elektronikus tudományos-technikai eszközök feloldóképessége ettől több nagyságrenddel elmarad. A lézertechnikában az utóbbi évtizedben lejátszódott fejlődés eredményeképpen előállíthatók olyan lézerimpulzusok, melyek segítségével ma már az elemi jelenségek kísérleti vizsgálata is lehetséges. Az esetek jó részében a megfelelő vizsgálathoz azonban nem elegendő a lézeroszcillátor által kibocsátott nJ nagyságrendű energia. Sőt, igazán izgalmas kísérletek, alapvető felfedezések elvégzéséhez nem csak 6-9 nagyságrenddel kell megnövelnünk a felhasználandó ultrarövid lézerimpulzus energiáját, hanem gondoskodnunk kell a nyaláb céltárgyra juttatásáról és a lehető legkisebb területre való torzulásmentes fókuszálásról is.
Az ultrarövid lézerimpulzusok alapkutatási felhasználása tehát alapvetően két területre osztható: egyrészt az elemi folyamatok időbontott vizsgálata (jelenleg szub-fs) mellett lézeres hűtés, lézercsipesz, stb. hozható létre, másrészt oly mértékű fókuszált intenzitás érhető el (1015-1022 W/cm2), mellyel egy sor rendkívül érdekes jelenség - az attoszekundumos impulzusok előállításától kezdve relativisztikus fény-plazma kölcsönhatásokon keresztül a lézer-indukált nukleáris reakciókig - idézhető elő.
A monokromatikus elektromágneses hullámok közegbeli terjedésének Maxwell-egyenleteken alapuló leírása a mai egyetemi törzsanyag része. Egy lézerimpulzus azonban hullámcsomagként fogható fel, azaz a Fourier-tétel szerint időben minél rövidebb, annál nagyobb a sávszélessége. A nagy sávszélesség, valamint az anyagok, eszközök diszperziós tulajdonságai miatt az általában használt lassan változó burkoló közelítés nem, vagy csak megszorításokkal érvényes. Ebben a digitális tananyagban a lézerimpulzusok rövidségéből fakadó lineáris, azaz intenzitás-független terjedés alapvető leírását körvonalazzuk, illetve az azzal kapcsolatos problémákat írjuk le. Elsősorban a jel alakjának időbeli formálódását tartván szem előtt a lézertechnikában használatos néhány alapvető optikai eszközre külön is kitérünk. Az összefüggések származtatásánál nem a klasszikus elektrodinamikában megszokott módon járunk el, azaz nem a Maxwell-egyenletek speciális megoldásaiból indulunk ki, hanem a jel terjedésére vonatkozó Fourier-transzformációs tételeket használjuk fel. Megközelítésünk oka, hogy lineáris rendszerek esetén a kétféle módszer ugyanazt a végeredményt adja, ugyanakkor a rendszerelméleti leírás matematikailag egyszerűbb, áttekinthetőbb, a paraméterek a mindennapi laboratóriumi gyakorlatban közvetlen jelentéssel bírnak.
E digitális tananyag célja, hogy a fent említett tudományterületnek, azaz a femtoszekundumos optikának az alapjaival megismertesse az Olvasót. A tananyag a Fizikus MSc szakos hallgatók Optika és lézerfizika moduljának egyik alapkurzusához, a Femtoszekundumos és nemlineáris optika alapjai című kurzushoz készült. A címből látható, hogy ez a tananyag a kurzusnak csak a lineáris optika részéhez tartozó ismereteket tartalmazza. A tananyag azon Biológus MSc és Vegyész MSc szakos hallgatók számára is hasznos információkkal szolgál, akik a diplomamunkájuk során femtoszekundumos lézerimpulzusokkal végeznek majd biológiai illetve kémiai kísérleteket. A tananyaghoz képest az előadás jóval részletesebben ismerteti a femtoszekundumos optika alapjait, ezért azt javasoljuk, hogy a kurzust is vegyék fel. Az előadáshoz közvetlenül nem kapcsolódik gyakorlat éppen abból a célból, hogy a különböző mesterszakokon tanuló hallgatóknak lehetőségük legyen választani, hogy e tudományterületet milyen mélységben kívánják elsajátítani.
Aki mélyebb ismeretekre is törekszik, itt különösen a Fizikus Msc szakos hallgatókra gondolunk, azok számára e témához kapcsolódóan további három kurzus választható, a Femtoszekundumos optika MathCad-del illetve a Lézerfizikai laboratóriumi gyakorlatok 1. és 2.. E kurzusok mind gyakorlati kurzusok. Míg az előbbi kurzus keretében a hallgatók az előadáson bemutatott jelenségek, eszközök működését az általuk készített számítógépes szimulációk segítségével, addig az utóbbi két, laboratóriumi gyakorlat típusú kurzusnál méréseket végezve részleteiben is megismerhetik. A jól sikerült szimulációk a későbbiekben a digitális tananyag részét is képezhetik majd.
A tananyag megértésének minimális előfeltétele, hogy az Olvasó rendelkezzen a természettudományi alapszakok bevezető fizikai és matematikai kurzusain elhangzó ismeretekkel. Természetesen, ha az Olvasó az említett kurzusokon kívül hallgatott még haladottabb szintű elektrodinamikai, optikai, lézerfizikai kurzust, akkor a tananyag elsajátítása könnyebbé válik. Itt különösen ki kell emelnünk, hogy ebben a tananyagban nem foglalkozunk a lézerek felépítésével, működésének jellemzőivel, az ultrarövid lézerimpulzusokat előállítására leggyakrabban használt lézertípussal, a Ti:zafír lézerrel, mivel erről a Fizika BSc szak Lézerek és alkalmazásaik illetve a Fizikus MSc szak törzsanyagához tartozó Lézerfizika című kurzusokon (illetve az utóbbihoz kapcsolódó digitális tananyagban) esik szó.
A tananyagban szereplő ismeretek hozzásegítik a hallgatókat, hogy szak befejezése után alkalmasak legyenek a korszerű technológiai alapanyagok és folyamatok femtoszekundumos lézerekkel történő vizsgálatára, a bennük lezajló fizikai jelenségek észlelésére, értelmezésére és alkalmazására.
A tananyag felépítése: az első három fejezetben az ultrarövid lézerimpulzusok jellemzésére használt fizikai mennyiségek definiálásával, jellemzőivel foglalkozunk. A 4. fejezetben rátérünk a lézerimpulzusok lineáris, homogén, diszperzív közegbeli terjedésének rendszerelméleti formalizmust használó leírására. Az 5. fejezetben a gyakrabban használt optikai elemek diszperziós tulajdonságait ismertetjük. A 6. fejezet az optikai elemek által okozott szögdiszperziónak az impulzus idő- és térbeli alakjára gyakorolt hatásáról szól. A 7. fejezetben bemutatjuk az ultrarövid lézerimpulzusok időbeli alakjának formálásra használt eszközöket, különös tekintettel a nagyintenzitású lézerimpulzusok előállítására alkalmazott fázismodulált impulzuserősítési technika két alapvető eszközét, az impulzusnyújtót és -kompresszort, melyek az impulzusok időbeli alakjának megfelelő kinyújtásáért és összenyomásáért felelősek. A 8. és 9. fejezetben áttekintjük az impulzusok kísérleti alkalmazásánál rendszerint fellépő fontos jelenségnek, az impulzusnak a céltárgyra, mintára történő fókuszálásával kapcsolatos problémákat. Az utolsó három fejezet méréstechnikai témájú. Míg a 10. fejezet az optikai elemek spektrális fázisfüggvényének, addig a 11. fejezet az optikai elemek által okozott szögdiszperziónak a mérési módszereit ismerteti. Az utolsó, 12. fejezet pedig az impulzus időbeli alakjának meghatározására szolgáló fontosabb technikákat mutatja be. A fejezetek végén ellenőrző kérdéseket találhatunk, melyek a fejezetben ismertetett fontosabb fizikai mennyiségekhez, jelenségekhez kapcsolódnak. Néhány esetben kérdés helyett számolási feladat szerepel, mellyel az Olvasó ellenőrizheti, hogy az ismeretanyagot készségszinten is tudja-e alkalmazni.
A tananyag elsajátításához alapvetően a lineáris tanulási módszert ajánljuk. Azon hallgatók, akik haladottabb optika, lézerfizika kurzuson is részt vettek, az első három fejezetet akár át is ugorhatják. Meg kell jegyeznünk, az 5. fejezet után némi szabadsága van az Olvasónak abban, hogy melyik fejezeteket tekinti át előbb. Ugyanis a 8. és 9. fejezet megértéséhez nem szükséges a 6. és 7. fejezetet elolvasni, míg a 10., 11. és 12. fejezet nem épül a 8. és 9. fejezet ismereteire, hanem csak az azt megelőzőkére.
Néhány megjegyzés a tananyagban található animációk, filmek megtekintésével kapcsolatban. Bár számos, multimédiás tartalmak lejátszására alkalmas program van forgalomban, azonban bizonyos programoknál az animációk lejátszásakor különféle hibákat észleltünk. Azért, hogy a tananyaghoz készült multimédiás tartalmak a tanulást segítsék, a nem interaktív animációk, hangfájlok és filmek megtekintésére a Windows Media Player-t ajánljuk. Az interaktív animációk esetében előbb le kell tölteni egy segédprogramot a lejátszáshoz. A szükséges segédprogram linkje az animáció mellett található.
A tananyag az Interdiszciplináris és komplex megközelítésű digitális tananyagfejlesztés a természettudományi képzési terület mesterszakjaihoz (TÁMOP-4.1.2.A/1-11/1) című projekt keretében készült.
Utolsó módosítás: 2013.05.13.

Tartalom
Ultrarövid fényimpulzusok alatt olyan lézerimpulzusokat értünk, melyek időbeli hossza néhány femtoszekundumtól (1 fs = 10-15s ) néhány száz pikoszekundumig (1 ps = 10-12s) terjed [1.1]. Ahhoz, hogy érzékeltessük, hogy az 1 fs milyen rövid időtartam, tekintsük a világunkban ismert leggyorsabb mozgást, azaz a fény terjedését. A fény vákuumban 1 fs alatt pusztán csak 300 nm távolságra jut el. A mindennapi életünket tekintve ez szinte felfoghatatlanul kicsi távolság. Egy kristály esetében azonban ez az érték néhány ezer elemi cella méretével egyezik meg.
Vegyünk egy másik példát, a hidrogénatomot. A Bohr-féle atommodellt tekintve, az atommag körül az n főkvantumszámú pályán keringő elektronnak az átlagos körüljárási ideje:
 |
. | (1.1) |
ahol e az elektron töltése, m e az elektron tömege és ε0 a vákuumpermittivitás. Ha a hidrogénatom gerjesztett állapotban van, például n =3, akkor a fenti kifejezés alapján a keringési időre T = 4 fs adódik. Ez az időtartam nagyjából megegyezik a Ti:zafír lézerrel eddig előállított legrövidebb fényimpulzus időtartamával.
Molekuláris skálán a kétatomos molekulák disszociációja során a kötésfelszakadás mellett a két atom kb. 1 km/s sebességgel távolodik egymástól. Ahhoz, hogy a molekulák a kötött állapotból izolált atomokká váljanak, néhány angströmnyi távolságra kell távolodniuk egymástól, ami azt jelenti, hogy ez a folyamat 100 fs-os időskálán zajlik le. Ebből következik, hogy ennek a jelenségnek a dinamikája néhány femtoszekundum időbeli hosszúságú lézerimpulzusokkal már tanulmányozható.
A femtoszekundumos optikában az előbb említett Ti:zafír lézer az egyik igen gyakran használt lézertípus. Ha az általa kibocsátott impulzusok spektrumát megvizsgáljuk, akkor a spektrum maximális értéke λ0=800 nm körül van. Egy ilyen hullámhosszú fényhullám periódusideje 2,7 fs. Ez annyit jelent, hogy a 6-10 fs időtartamú impulzusok csak néhány periódusból állnak, ellentétben a nano- illetve pikoszekundumos időtartamú lézerimpulzusokkal. Nemrég kiderült, hogy amikor csak néhány periódusból áll egy lézerimpulzus, akkor a fény-anyag kölcsönhatás szempontjából már korántsem mindegy, hogy az impulzus térerősségének burkológörbéje alatt hol helyezkedik el a térerősség maximális csúcsa.
Egy átlagos Ti:zafír lézer impulzusainak időtartama 10 fs körül van. Ha geometriai méretekben gondolkodunk, azaz mintha lefényképeznénk az előttünk elhaladó fényimpulzust, akkor ez az impulzus 3 μm hosszúságú, miközben az átmérője tipikusan néhány milliméter. Ez azt jelenti, hogy úgy képzelhetjük el ezeket az impulzusokat, mintha egy szalvéta repülne el előttünk a levegőben. Ahogy a szalvéta alakja rendkívül érzékenyen reagál még a legenyhébb légáramlatokra is, az ultrarövid lézerimpulzus idő- és térbeli alakja is nagyon könnyen torzulhat a terjedése során. Ezért komoly elméleti és kísérleti vizsgálatokat végeztek az impulzusok terjedésével kapcsolatban, illetve számos eszközt fejlesztettek ki, amelyek az impulzus idő- és a térbeli alakjában bekövetkező változásokat diagnosztizálják, illetve korrigálják. Ezen technikákról illetve eszközökről a későbbi fejezetekben olvashatunk.
Végül tekintsünk egy szintén fontos paraméterét a lézerimpulzusnak, a csúcsintenzitást. Manapság egy erősített lézerimpulzusokat produkáló lézerrendszer kimenetén az impulzusok időtartamának és energiájának tipikus értékei 50 fs illetve 1 mJ, azaz a teljesítményük 20 GW. Ezeknek az impulzusoknak az átmérője 1 cm körül van. Az impulzus fókuszálására használjunk egy 10 cm fókusztávolságú lencsét. Ekkor a fókuszfolt átmérője 10 μm körüli érték, azaz a felülete 80 μm2. Ebből következően az intenzitás 25 PW/cm2, ami kb. 4 GV/cm térerősséget eredményez. Ha ezt összevetjük az atomon belüli térerővel, ami 1 GV/cm nagyságrendbe esik, akkor láthatjuk, hogy egy erősített femtoszekundumos impulzust, ha ráfókuszálunk az anyagra, akkor olyan térerősséget hozunk létre, ami összemérhető az atomon belüli térerősséggel, így a megvilágítás befolyásolhatja az elektronok mozgását. Az anyagot egy másik lézerrel megvilágítva, azaz egy pumpa-próba kísérletet elvégezve, az anyag szerkezetéről fontos információkat szerezhetünk.
Bár az előbbi példában egy erősített impulzust tekintettünk, azonban a Ti:zafír lézerből kilépő impulzusok bár kicsiny energiájúak, de az extrém rövid időtartamuk miatt a csúcsintenzitásuk a minket körülvevő fényhullámokhoz képest jelentős. Ez azt eredményezi, hogy a fény-anyag kölcsönhatás során az anyag válasza a lézerimpulzus gerjesztésére a nemlineáris tartományba kerül, azaz nemlineáris optikai jelenségek is bekövetkeznek. Ilyen jelenség például a felharmonikus keltés, amikor infravörös hullámhosszú, ultrarövid időtartamú lézerimpulzust fókuszálunk rá egy kettősen törő BBO (béta-bárium-borát) kristályra, és a kristály túloldalán ultraibolya hullámhosszú lézerimpulzus is megjelenik az eredeti impulzus mellett. Bár a keletkezett ultraibolya fényt a szemünk nem érzékeli, azonban ha egy fehér papírt teszünk a fény útjába, akkor az ultraibolya fény hatására kékesen fluoreszkálni kezd. Egy másik példa, amikor egy kvarclemezre fókuszáljuk az ultrarövid lézerimpulzust, és vakító fehér fényben világít a kvarclemezen a fókuszfolt. Ezt a jelenséget úgy hívjuk, hogy fehérfény-kontinuum keltése. Ilyen módon rendelkezésünkre áll már egy, a hagyományos fehér lámpához hasonlóan széles spektrummal bíró fényforrás, azonban ez a fény jól kollimálható, jóval nagyobb az intenzitása és a térbeli koherenciája a hagyományos lámpával összehasonlítva.
A fenti példák azt mutatják, hogy az ultrarövid lézerimpulzusok igen fontos szerepet töltenek be az anyagszerkezeti kutatásokban [1.2],[1.3], de számos orvosi alkalmazással is találkozhatunk [1.4]. Egyre szélesebb körben használják őket, ezért egy lézerfizikával foglalkozó kutatónak fontos, hogy ismerje ezen impulzusok terjedésének jellemzőit, diagnosztikai módszereit. A további fejezetekben e területeket tekintjük át röviden.
[1.1] J-C. Diels, W. Rudolph: Ultrashort laser pulse phenomena, 2. kiadás (Academic Press, 2006)
[1.2] W. Demtröder: Laser spectroscopy, 3. kiadás (Springer, 2004)
[1.3] J. M. Hollas: Modern spectroscopy, 4. kiadás (John Wiley, 2004)
[1.4] M. E. Ferman, A. Galvanauskas, G. Sucha szerk.: Ultrafast lasers, Technology and applications (Marcel Dekker, 2001)
A femtoszekundumos fényimpulzusok elektromágneses hullámcsomagok, ezért az idő- és térfüggő elektromos térerősséggel teljesen leírhatók. A fényimpulzusok terjedésének és anyaggal való kölcsönhatásának tárgyalásánál a Maxwell-egyenletekkel írjuk le a terjedést. Az anyagnak a fényimpulzusra adott válaszát a makroszkopikus polarizációval vesszük figyelembe. Ebben a fejezetben összefoglaljuk a fontosabb jelöléseket és fogalmakat. Az impulzusokat mérhető mennyiségekkel jellemezzük, melyek közvetlenül kapcsolhatók az elektromos térerősséghez. Bár a mérhető mennyiségek valósak, a térerősség felírásakor mégis a komplex írásmódot használjuk, ami kényelmesebbé teszi a fényimpulzusok terjedésének leírását.
Tekintsük először az elektromos térerősséget csak, mint az idő függvényét, azaz eltekintünk a térfüggéstől és a polarizációtól:
 |
. | (2.1) |
ahol E(t) valós mennyiség. Definiáljuk a térerősség komplex spektrumát a Fourier-transzformáció segítségével:
 |
. | (2.2) |
ahol |Ę(ω)| jelöli a spektrális amplitúdót , és a Φ(ω)-t spektrális fázisnak nevezzük. Itt is és a következőkben is ^ jelöli, hogy komplex mennyiségről van szó.
Mivel E(t) valós, ezért teljesül, hogy
 |
. | (2.3) |
Ha adott a térerősség komplex spektruma, akkor abból az inverz Fourier-transzformáció segítségével kapjuk meg az elektromos térerősség időfüggését, azaz
 |
. | (2.4) |
Gyakorlati szempontból nem túl kényelmes olyan függvényeket használni, amelyek értéke zérustól különbözik a negatív frekvenciák esetében, ami például a (2.4)-nél is előállhat. Gyakran az E(t) időfüggő elektromos térerősségnél is hasznos, ha komplex írásmódot használunk. A fenti két követelménynek eleget tehetünk, ha az alábbi módon vezetjük be a komplex térerősséget :
 |
. | (2.5) |
ahol a megfelelő spektrális térerősség csak pozitív frekvenciákat tartalmaz:
 |
. | (2.6) |
Vegyük észre, hogy ekkor
 |
. | (2.7) |
és
 |
. | (2.8) |
Hasonlóan az Ę-(t) és Ę-(ω) is definiálható. A valós térerősség az alábbi módon fejezhető ki ezekkel az újonnan definiált mennyiségekkel:
 |
. | (2.9) |
és a komplex értékű Fourier-transzformáltjaik közötti kapcsolat:
 |
. | (2.10) |
Az Ę+(t) -t általában egy amplitúdó és egy fázistag szorzataként írhatjuk fel:
 |
. | (2.11) |
A gyakorlatban a spektrális amplitúdó csak egy ω0 frekvencia körüli Δω intervallumban nem lesz zérus, így érdemes bevezetni az ω0 - t, mint vivőfrekvenciát , és ekkor
 |
. | (2.12) |
ahol φ(t) az időfüggő fázis , Ԑ(t)a valós amplitúdó burkoló , míg a ^-pal jelölt mennyiség a komplex változata. A konstans eiφ0 fázistagnak, melyet vivő-burkoló fázistagnak nevezünk, gyakran nincs jelentősége, és így akár el is hagyható. Azonban amikor néhány optikai ciklusú lézerimpulzusok hatnak kölcsön az anyaggal, ez a tag jelentősen befolyásolja a kölcsönhatás eredményét. Ebből következőleg ilyen esetekben a vivő-burkoló fázis mérése és kontrollja igen fontos.
Csak abban az esetben hasznos a vivőfrekvencia és burkológörbe fogalmának bevezetése, ha az impulzus spektrumának sávszélessége töredéke a vivőfrekvencia értékének, azaz
 |
. | (2.13) |
Ez azt jelenti, hogy Ԑ(t) és φ(t) változásának egy optikai cikluson belül (ami T =2,7 fs körüli érték egy Ti:zafír lézer esetében) kicsinek kell lenni. Ennek a követelmények eleget teszünk, ha
 |
. | (2.14) |
amit lassan változó burkoló közelítésnek (slowly varying envelope approximation, SVEA) nevezünk.
Figyelembe véve, hogy manapság a legrövidebb impulzusok néhány optikai ciklusból állnak, ilyen esetekben körültekintően kell eljárnunk, hogy a SVEA közelítés megfelelően leírja-e az impulzus viselkedését. Ha igen, akkor az impulzus terjedésének illetve az anyaggal való kölcsönhatásának a leírása nagyban egyszerűsödik.
Legyen adott a Ę+(ω) komplex spektrális amplitúdó. Ekkor az időfüggő térerősség komplex amplitúdó burkolóját (2.7) és (2.12) alapján az alábbi Fourier-transzformációból kapjuk meg:
 |
. | (2.15) |
azaz az integrandusban eltoltuk a komplex spektrális amplitúdó függvényt ω0 -lal a frekvencia tengely mentén. Az optimális értéke az ω0 transzlációnak az, amelynél a burkológörbében a legkevesebb moduláció van.
Ezután vizsgáljuk meg a fizikai jelentését a φ(t) fázisfüggvénynek. Az ω0 központi vivőfrekvencia megválasztásának olyannak kell lenni, hogy minimalizálja a φ(t) fázis változását. A (2.11)-ben szereplő Γ(t) fázisfaktornak az idő szerinti első deriváltja megadja a pillanatnyi vivőfrekvenciát :
 |
. | (2.16) |
Ha a dφ/dt egy állandó b érték, akkor ez azt jelenti, hogy a pillanatnyi vivőfrekvencia időben állandó, de a központi vivőfrekvenciához képest b-vel eltolódik. Ha a dφ/dt = f(t), azaz időben változik, akkor a pillanatnyi vivőfrekvencia is változni fog időben. Ekkor az impulzust frekvenciamoduláltnak vagy más néven csörpöltnek nevezzük (angolul chirp). Tehát a csörp a pillanatnyi frekvencia változási gyorsaságát jellemzi. Ha a d2φ/dt2 >0 vagy <0, akkor a vivőfrekvencia időben nő vagy csökken, azaz ekkor pozitívan (up) vagy negatívan (down) csörpöltnek nevezzük az impulzust.
(2.11)-ből látható, hogy Γ(t) felbontása ω0-ra és φ( t )-re nem egyértelmű A legeredményesebb felbontás az, amikor a legkisebb dφ/dt adódik az impulzusnak a legintenzívebb részén. Általában ω0az impulzuscsúcsnál vett vivőfrekvencia értékével egyezik meg. Ennél egy jobb definíció, amely konzisztens mind az idő- mind a frekvenciatartományban, amikor egy intenzitás-súlyozott átlagot használunk:
 |
. | (2.17) |
Az ebben a fejezetben bevezetett jelöléseket szemlélteti a 2.1. és a 2.2. ábra. A 2.1.a ábrán láthatjuk egy néhány ciklusból álló, ultrarövid lézerimpulzus E(t) térerősségének időbeli alakját. Az ábrán a kék szaggatott vonal az elektromos térerősség Ԑ(t) burkológörbéjét jelöli. A 2.1.b ábra a 2.1.a ábrán látható impulzus vivőfrekvenciájának időfüggését ábrázolja. Vegyük észre, hogy a vivőfrekvencia változik időben, méghozzá monoton módon növekszik, azaz a 2.1.a ábrán látható térerősség egy pozitívan csörpölt impulzus térerőssége. Ezt persze már a 2.1.a ábrán is észrevehetjük, mivel az impulzus elején a hullám periódusideje láthatóan jóval nagyobb, mint az impulzus végén.

2.1. ábra a) Egy pozitívan csörpölt ultrarövid lézerimpulzus térerősségének (piros vonal) időbeli alakja, feltüntetve a térerősség burkológörbéjét is (kék vonal). b) Az impulzus vivőfrekvenciájának időbeli változása.
Végezzük el a 2.1.a ábrán látható E(t) térerősségen a Fourier-transzformációt. A kapott komplex értékű Ę(ω) függvény abszolút értéke megadja a spektrális amplitúdót (2.2.a ábra), illetve a fázisa a spektrális fázist (2.2.b ábra). Míg az |Ę + (ω)| függvénynek a tükörképe az |Ę-(ω)| függvény, addig a spektrális fázis esetében ez így nem igaz. Ekkor a (2.3) egyenletből következően, ha a Φ-(ω) függvényt -1-gyel megszorozzuk, akkor már valóban a tükörképét kapjuk a Φ+(ω) spektrális fázisgörbének, ahogy a 2.2.b ábrán is láthatjuk.
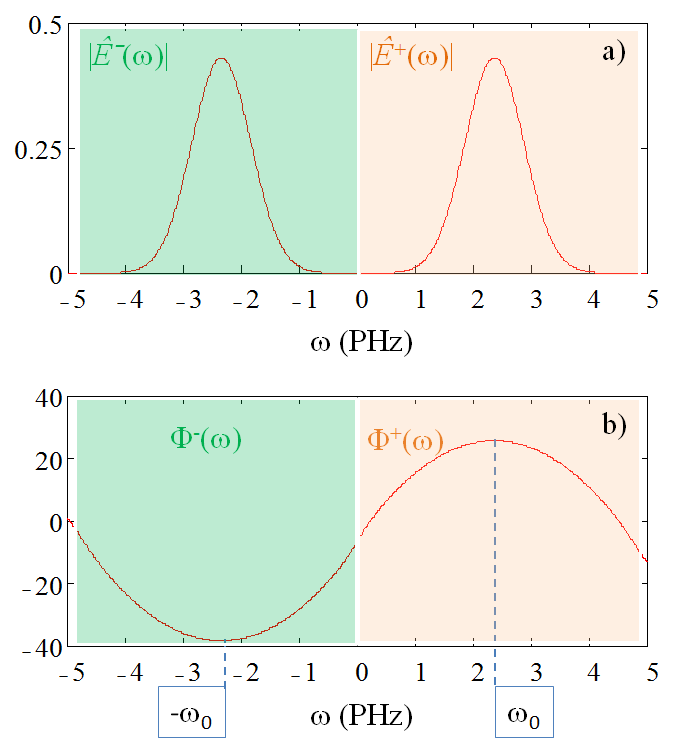
2.2. ábra Pozitívan csörpölt impulzus 2.1. ábrán látható térerősségének Fourier-transzformációjával kapott a) spektrális amplitúdó és b) spektrális fázis.
Tekintsük azt az esetet, amikor az impulzus egy A keresztmetszetű nyalábban terjed, és az elektromos térerőssége E(t). Az impulzus (pillanatnyi) teljesítménye (wattban megadva) egy n törésmutatójú, diszperziómentes közegben a Poynting-vektorból számolva:
 |
. | (2.18) |
ahol c a vákuumbeli fénysebességet jelöli. Az integrálást a nyaláb teljes keresztmetszetére el kell végeznünk, mivel a mérendő impulzus teljes keresztmetszetében megvilágítja a teljesítmény mérésére használt detektor (fotodióda, fotoelektronsokszorozó, stb.) fényérzékeny felületét. A detektor időbeli válaszának olyan rövidnek kell lenni, mint a mérendő impulzus térerősségének periódusideje ( T =2π/ω0). Az időbeli átlagolást erre a T időtartamra kell elvégezni. Vegyük észre, hogy a (2.18) egyenlettel bevezetett pillanatnyi teljesítmény egy megfelelő elméleti mennyiség. Azonban a gyakorlati életet tekintve, a detektorok τR válaszideje sokkal nagyobb T-nél, ezért (2.18)-ban T helyett τR-t kell használnunk. Még a napjainkban elérhető leggyorsabb detektorokkal (τR~10-13-10-12s) sincs lehetőségünk arra, hogy az ultrarövid lézerimpulzusok időbeli burkolójának részleteit közvetlenül kimérjük.
A teljesítmény időbeli integrálása az impulzus energiáját adja meg (jouleban):
 |
. | (2.19) |
ahol az integrálási határokat a mérendő impulzus előtti és utáni időpillanatok adják.
A megfelelő mennyiség az egységnyi felületen átáramló teljesítmény, azaz a pillanatnyi intenzitás (W/cm2):
 |
. | (2.20) |
valamint az egységnyi felületen átáramló energia, azaz az energiasűrűség (J/cm2):
 |
. | (2.21) |
Néhány esetben hasznos, ha olyan mennyiségeket használunk, amik a fotonszámmal vannak kapcsolatban, azaz az f fotonfluxus (foton/s) vagy az F fotonfluxus sűrűség (foton/s/cm2):
 |
. | (2.22) |
ahol ω0 az impulzus vivőfrekvenciájával rendelkező foton energiája.
Az impulzusok spektrális tulajdonságainak vizsgálatához rendszerint egy spektrométert használunk, melynek a kimenetén például egy diódasort helyezünk el. A diódasor egy-egy pixelére az impulzus teljes spektrumának egy-egy kicsiny frekvenciatartományú része esik, azaz a detektor a I(ω) spektrális intenzitást méri időfelbontás nélkül:
 |
(2.23) |
ahol az η egy skálázási faktor, melynek értéke függ a detektor spektrális érzékenységétől és a spektrográf felbontóképességétől. Vegyük észre, hogy I(ω) nem az I(t) függvény Fourier-transzformáltja, azaz az I(ω) jelölés nem teljesen konzekvens a korábbi jelöléseket tekintve. Azonban a szakirodalomban ezt a jelölést használják leggyakrabban, így mi is ezt használjuk a továbbiakban.
Egy ideális spektrométert tekintve az η értéke meghatározható az energiamegmaradás törvényét
 |
. | (2.24) |
és a Parseval-tételt
 |
. | (2.25) |
használva, melyekből adódik, hogy
 |
. | (2.26) |
A komplex Ę+ mennyiséget használjuk a továbbiakban az impulzus elektromos térerősségének leírására. A jelölések egyszerűsítése céljából, ahol ez nem zavaró, a + jelet elhagyjuk.
Hogyan kapjuk meg a spektrális amplitúdót az impulzus térerősségének időfüggéséből?
Hogyan definiáljuk az impulzus pillanatnyi vivőfrekvenciáját?
Mit jelent az, hogy egy lézerimpulzus negatívan vagy pozitívan csörpölt?
Milyen esetekben használható a lassan változó burkoló közelítés?
Igazolja a (2.3) egyenlet helyességét!
Hogyan számoljuk ki az impulzus pillanatnyi intenzitását?
Mi a különbség a pillanatnyi intenzitás és a spektrális intenzitás között?
Mondja ki a Parseval-tételt!
Tartalom
Az előző fejezetben bevezettük az intenzitás illetve a spektrális intenzitás fogalmát. Míg az előbbi az impulzus időbeli alakját, addig az utóbbi a spektrumának alakját adja meg. Ezek a függvények különböző impulzusok esetén különböző menetűek. Ahhoz, hogy össze tudjuk hasonlítani különböző impulzusok időbeli alakját illetve spektrumát, célszerű bevezetni olyan mennyiségeket, melyek esetében egy-egy számmal jellemezhetjük az alakot [3.1, 3.2].
Az impulzus időtartama, időbeli hossza vagy más néven időbeli félértékszélessége alatt azt a τp időtartamot értjük, amíg az impulzus I(t) intenzitása a maximális értékének a felénél nagyobb értékű (full width at half maximum, FWHM) (3.1.a ábra). Az impulzus Δωp spektrális sávszélessége alatt pedig annak a két körfrekvencia értéknek a különbségét értjük, amelyek között teljesül, hogy az I(ω) spektrális intenzitás értéke nagyobb a maximális érték felénél (3.1.b ábra).

3.1. ábra Egy lézerimpulzus a) időbeli hosszának és b) spektrális sávszélességének definíciója. Az ábrán látható impulzus csörpölt, időbeli hossza 10 fs, míg a sávszélessége 0,85 PHz.
Az impulzusok jellemzése e mennyiségekkel akkor igazán hasznos, ha az impulzus időbeli alakja illetve a spektrumának alakja haranggörbe jellegű.
Ennek a feltételnek eleget tesz az egyik igen gyakran használt impulzusmodell, a Gauss-görbe lefutású impulzus (lásd 3.1.a ábra), ahol a térerősség burkológörbéjének egyenlete:
 |
. | (3.1) |
Az impulzus időbeli alakja és a spektruma között a Fourier-transzformáció teremt kapcsolatot. Ebből következően az impulzus τp időtartama és a Δωp=2πΔνp spektrális sávszélessége nem változtatható egymástól függetlenül, van egy minimális sávszélesség-időtartam szorzat, ami ebben az esetben
 |
. | (3.2) |
Az egyenlőségjel a csörpöletlen impulzusokra érvényes, amelyeket transzformlimitált, sávszélesség limitált vagy Fourier-limitált impulzusoknak hívunk. Ezek az impulzusok rendelkeznek a legrövidebb időtartammal egy adott spektrális sávszélesség mellett. Vegyük észre, hogy a 3.1. ábrán látható impulzus esetében a szorzat értéke 1,35, azaz jóval nagyobb a 0,441 értéknél. Ez azt mutatja, hogy az impulzus csörpölt.
Vizsgáljuk meg ezek után a lineáris csörp hatását, mely analitikusan is jól kezelhető. Az impulzus térerősségének burkolója ekkor (3.1)-et kiírva:
 |
. | (3.3) |
ahol a a lineáris csörp paraméter, melynek az értéke pozitív a negatívan csörpölt impulzusokra, mivel
 |
. | (3.4) |
A (3.3) Fourier-transzformáltja:
 |
(3.5) |
ahol a Φ(ω) spektrális fázis:
 |
(3.6) |
Vegyük észre, hogy a spektrális fázist lineáris csörp esetén körfrekvenciában másodfokú függvény írja le.
Látható (3.5)-ből, hogy a spektrális intenzitás is Gauss-görbe alakú:
 |
(3.7) |
melynek a félértékszélessége
 |
(3.8) |
Ekkor az impulzus időtartamának és sávszélességének szorzata:
 |
(3.9) |
melyből nyilvánvaló, hogy a szorzat értéke a=0-nál, azaz csörpöletlen impulzus esetén a legkisebb, összhangban (3.2)-vel. Ez persze azt is jelenti, hogy ha csörpölt lesz az impulzus, akkor újabb spektrális komponensek jelennek meg, így szélesedik a spektrum, és az időtartam-sávszélesség szorzat értéke is nő. Eddigiekben egy speciális impulzusalakot, a Gauss-görbe alakot vizsgáltuk meg. Ezek után térjünk rá az általánosabb eset vizsgálatára.
Számos esetben a korábban bevezetett impulzushossz és sávszélesség definíció nem igazán jól használható az impulzus jellemzésére. Ha az impulzuson belül van egy szubstruktúra (3.2.a ábra), vagy éppen széles talpai vannak (3.2.b ábra), amikben viszonylag sok energia raktározódik el, az időbeli félértékszélesség illetve a sávszélesség lehet ugyanakkora, miközben az impulzus fizikai hatása jelentősen eltérő lehet. Ezekben az esetekben egy átlagolt másodrendű momentum használata célszerűbbnek tűnik.

3.2. ábra Két 29 fs időbeli félértékszélességű, de eltérő spektrális fázisú impulzus időbeli alakja. Amikor a spektrális fázis körfrekvenciában a) harmadrendű függvény, akkor mellékimpulzus sorozatot alakul ki, míg b) ha negyedrendű függvény, akkor talpai lesznek az impulzusnak.
Először tekintsük általánosan egy f(x) függvényt, ahol az x jelölheti a térkoordinátát, az időt vagy éppen frekvenciát. Az x mennyiség n-ed rendű intenzitás szerinti momentuma:
 |
(3.10) |
Az n=1 eset, azaz az első rendű momentum az intenzitás-eloszlás tömegközéppontját adja meg, amit gyakran úgy választanak, hogy ez legyen a referencia pont, azaz a 0 értékű koordináta tartozzon hozzá. Például a (3.1)-gyel leírt, időben Gauss-görbe alakú impulzus esetén t=0-nál van a csúcsa az intenzitásgörbének. Egy jó választásnak tűnik az eloszlásfüggvény szélességének a jellemzésére az átlagos négyzetes eltérés, azaz
 |
(3.11) |
Ennek alapján az időbeli szélességre és a spektrális sávszélességre adódik, hogy
 |
. | (3.12) |
és
 |
(3.13.) |
Amikor lehetséges, feltételezzük majd, hogy az elsőrendű momentum zérus, azaz
 |
(3.14) |
Van egy jól ismert határozatlansági elv a konjugált változók másodrendű momentumai között. Ha k a Fourier-konjugált párja az x változónak, akkor megmutatható, hogy
 |
(3.15) |
ahol bevezettük az M2 alakfaktort, amelyet a Gauss-nyalábok jellemzésére szoktak használni [3.2]. A (3.15) reláció alkalmazható az időre és a frekvenciára, mint konjugált párokra is:
 |
(3.16) |
Az egyenlőség csak a fázismoduláció nélküli Gauss-os impulzusokra (nyalábokra) érvényes. Fontos megjegyezni, hogy a (3.15) és (3.16) határozatlansági relációk csak arra az impulzusszélességekre érvényesek, amelyek (3.11) szerint vannak definiálva. Gauss-os impulzusokra
 |
(3.17) |
míg a félértékekkel definiált szélességek szorzatára (3.2) szerint 0,441 adódott. A szorzat értéke a Gauss-os impulzusok esetén nem minimális, mivel szekáns hiperbolikusz vagy Lorentz-görbe esetében kisebb. Azonban az igaz, ha csak a Gauss-görbe alakú impulzusokat tekintjük, akkor a szorzat abban az esetben minimális, ha nincs frekvenciamoduláció, ahogy ezt már korábban tárgyaltuk.
A kvadratikus fázismoduláció fontos szerepet játszik az impulzus idő- és térbeli terjedésében egyaránt. Egy szférikus hullámfront jól közelíthető egy kvadratikus fázissal a terjedési irány közelében, mely a nyaláb fókuszálódásához vagy defókuszálódásához vezet. Ez az analógia igaz időben is, azaz kvadratikus fázismoduláció az impulzus időbeli összenyomódásához vagy éppen kiszélesedéséhez vezet, miközben keresztülhalad egy diszperzív közegen. A továbbiakban ez utóbbit vizsgáljuk meg részletesebben.
Vegyünk egy transzformlimitált impulzust, mely keresztülhalad egy diszperzív közegen, és ennek során kvadratikus fázismodulációra tesz szert. Tételezzük fel, hogy a közeg az impulzus amplitúdó- illetve teljesítményspektrumát nem befolyásolja. Az impulzus spektruma az <ω>=ω0 átlagfrekvencia körül koncentrálódik. Az átlagfrekvencia nem változik, ennél fogva a Φ(ω) függvény Taylor-sorának első nem zérus tagja:
 |
(3.18) |
ahol Φ(ω) meghatározza az Ɛ(ω) fázisfaktorát:
 |
(3.19) |
Az első- és a másodrendű momentumok (3.10) szerint:
 |
(3.20) |
és
 |
(3.21) |
A fenti formulákban a ' jel az ω szerinti deriválást jelzi. Mivel az impulzus kezdetben transzformlimitált volt, és a spektrumát a diszperzív közeg nem változtatta meg, így (3.21) első tagja a t-nek a közegbe való belépés előtti <t 2 >0 másod rendű momentumát adja meg. Behelyettesítve a fázisra kapott (3.18) kifejezést (3.10)-be, a t másodrendű momentumára kapjuk, hogy
 |
(3.22) |
azaz a frekvenciacsörp időbeli kiszélesedést okoz, ami arányos a csörpegyüttható négyzetével.
Ezen formalizmussal az időbeli fázismodulációnak
 |
(3.23) |
a spektrumra gyakorolt hatása is vizsgálható, ha az impulzus időbeli burkológörbéje változatlan marad. Az időbeli frekvenciamoduláció vagy csörp spektrális kiszélesedéshez vezet:
 |
(3.24) |
ahol <ω2>0 a közegbe belépő impulzus spektrális sávszélességét jelöli. A (3.22) és (3.24) kifejezések az időbeli hossz és sávszélesség (3.11)-en alapuló definícióinak hasznosságát mutatja, mivel látható, hogy egyszerű kapcsolatot teremt az időbeli és a spektrális kiszélesedés között úgy, hogy függetlenné vált az impulzus időbeli alakjától illetve a spektrumának alakjától.
A (3.22)-re és a (3.24)-re alkalmazhatjuk a (3.16)-tal adott határozatlansági relációt:
 |
(3.25) |
ahol bevezettük a κc csörpparamétert, melynek értéke frekvenciacsörp esetén, állandó spektrum mellett:
 |
(3.26) |
 |
(3.27) |
és időbeli csörp esetén, ha az impulzus időbeli burkológörbéjének alakja állandó
Összefoglalva, ha az átlagos négyzetes eltérést használjuk az impulzushossz és a sávszélesség definiálására, akkor:
-
az impulzushossz-sávszélesség szorzat

minimális, ha nincs frekvenciamoduláció. Gauss-os impulzusokra a minimális érték 0,5.
bármilyen impulzusalakra definiálhatunk egy M2 alakfaktort, ami egyenlő a minimális hossz-sávszélesség szorzattal.
bármilyen kvadratikus fázismoduláció vagy lineáris csörp akár az idő-, akár a frekvenciatartományban megnöveli a hossz - sávszélesség szorzatot a κc csörpfaktorral. A csörpfaktor arányos a fázis idő illetve frekvencia szerinti második deriváltjával.
Hogyan szokás definiálni Gauss-görbe alakú impulzusokra az impulzus időbeli szélességét illetve a spektrális sávszélességét?
Az 1. kérdésben említett definíciók alkalmazása általános alakú impulzusnál miért okozhat problémát?
Hogyan definiáljuk az impulzus időbeli és spektrális szélességét általános esetben?
Transzformlimitált impulzus esetében mekkora az időbelihossz-sávszélesség szorzat értéke a két eltérő definíció esetében?
Mit okoz az időben kvadratikus csörp az impulzus spektrumában, ha az intenzitásának időbeli burkológörbéje nem változik?
Mit okoz a frekvenciában kvadratikus csörp az impulzus időbeli alakjában, ha a spektrumának alakja nem változik?
Tartalom
Az ultrarövid impulzusok közegbeli terjedésének leírását a Maxwell-egyenletekből levezethető hullámegyenlet megoldásaként tárgyalhatjuk az elektromos térerősség időbeli alakjának megadásával. Abban az esetben, ha az impulzus lineáris optikai elemen halad keresztül vagy verődik vissza róla, akkor a lineáris rendszerek leírására kidolgozott formalizmust használhatjuk, mely megkönnyíti a terjedés során lezajló folyamatok megértését és egyszerű matematikai alakba öntését. Az optikai elrendezésekben gyakran használt elemek többsége lineáris optikai elem, például tükör, prizma, diffrakciós rács. Ebben a fejezetben az impulzusoknak a lineáris optikai elemen való áthaladás során bekövetkező időbeli és spektrális változásait vizsgáljuk, azaz eltekintünk a nyalábjellemzők esetleges változásaitól.
Egy lineáris optikai elem jellemezhető a
 |
(4.1) |
komplex optikai átviteli függvényével, amely összekapcsolja az optikai elembe belépő impulzus Ębe(ω) illetve az abból kilépő impulzus Ę(ω) komplex térerősség spektrumát:
 |
(4.2) |
Itt R(ω) a valós értékű amplitúdóátviteli függvény, míg a Φ(ω) az optikai elem spektrális fázisfüggvénye. Amint látható (4.2)-ből, az R(ω) hatása az, hogy megváltoztatja az optikai elemen áthaladó impulzus ω frekvenciájú spektrális komponensének amplitúdóját, azaz frekvenciaszűrőként viselkedik. A Φ(ω) fázisfaktor úgy interpretálható, mint az ω frekvenciájú spektrális komponens átal elszenvedett fáziskésés. Ahhoz, hogy a Φ(ω)-nak az impulzus időbeli alakjára gyakorolt hatását jobban lássuk, tegyük fel, hogy R(ω) értéke nem függ a frekvenciától a vizsgált spektrumtartományban. Így az optikai elemből kilépő impulzus térerősségének időfüggésére kapjuk, hogy
 |
(4.3) |
Amennyiben az optikai elem Φ(ω) spektrális fázisfüggvénye bizonyos matematikai feltételeknek eleget tesz, akkor Taylor-sorba fejthető az impulzus ω0 központi frekvenciája körül:
 |
(4.4) |
Az optikai elem diszperziós tulajdonságait a Taylor-sor együtthatóival, a fázisderiváltakkal jellemezzük. A fázisderiváltak elnevezése ahol lehet, kapcsolódik az impulzus időbeli alakjára gyakorolt hatásukhoz. Így a
 |
(4.5) |
azaz a spektrális fázisnak a körfrekvencia szerinti elsőrendű deriváltját csoportkésleltetésnek (group delay -GD), míg a
 |
(4.6) |
másodrendű fázisderiváltat csoportkésleltetés-diszperziónak (group delay dispersion -GDD) nevezzük. A harmad- és magasabb rendű deriváltak esetében az elnevezés a derivált rendjére utal, azaz a
 |
(4.7) |
harmadrendű deriváltat egyszerűen csak harmadrendű diszperziónak (third order dispersion -TOD) hívjuk. Az optikai elem spektrális fázisának (4.4)-gyel adott Taylor-sorát beírva (4.3)-ba és némileg átrendezve kapjuk, hogy
 |
(4.8) |
A (4.8) kifejezésből látható a spektrális fázisfüggvény sorfejtésében szereplő nullad- és elsőrendű tagnak a hatása. A nulladrendű tag, azaz az e-iΦ0 egy konstans fázistag, aminek nincs hatása a térerősség burkológörbéjének alakjára. Azonban befolyásolja, hogy a burkológörbe alatt a térerősség maximuma hol helyezkedik el. Az elsőrendű derivált (GD) az impulzus időbeli késését okozza, azaz egy csoportsebességgel terjedő hullámcsoportnak GD időre van szüksége ahhoz, hogy a lineáris optikai elemen áthaladjon. Ezért hívjuk az elsőrendű deriváltat csoportkésleltetésnek. A magasabb rendű fázisderiváltak a körfrekvenciában nemlineáris spektrális fázisfüggvényt eredményeznek, ami a térerősséget burkológörbe alakjának megváltozását illetve az impulzus csörpölődését okozza.
Általános esetben nem lehet analitikus formát kapni a magasabb rendű fázisderiváltak által létrehozott impulzusalakra. Azonban, ha Gauss-os időbeli lefutású impulzus alakjának megváltozását vizsgáljuk, és a spektrális fázist csak másodrendű tagig vesszük figyelembe, akkor már zárt alakot kapunk. Az egyszerűség kedvéért tételezzük fel, hogy a lineáris optikai elemhez érkező impulzus transzformlimitált is, azaz a térerősségének időfüggése:
 |
(4.9) |
ahol τp0 jelöli az impulzus időbeli félértékszélességét az optikai elembe való belépés előtt. Az impulzus térerősség spektrumát a (4.9)-en Fourier-transzformációt elvégezve kapjuk meg:
 |
(4.10) |
Vegyük észre, hogy (4.10)-ben az egyenlőségjel baloldalán a térerősséget komplex mennyiségként jelöltük, miközben a jobb oldalon valós mennyiség szerepel. Ezt azért hagytuk így, mert arra utalunk, hogy általános esetben a térerősség spektrum komplex értékű, és csak ebben a speciális esetben vált valós értékűvé, mivel a spektrális fázisfüggvény értéke zérus.
Az optikai elem spektrális fázisfüggvénye csak másodrendig tartalmazzon tagokat, azaz:
 |
(4.11) |
Szintén az egyszerűsítés kedvéért tételezzük fel, hogy az optikai elem az impulzus spektrális komponenseinek amplitúdóját nem változtatja meg, azaz R=1. Az optikai elemből kilépő impulzus térerősségének időbeli függését megkapjuk, ha (4.10)-et és (4.11)-et (4.3)-ba helyettesítjük, és elvégezzük az inverz Fourier-transzformációt:
 |
(4.12) |
ahol a térerősség-burkoló maximális értéke:
 |
(4.13) |
az impulzus időbeli félértékszélessége:
 |
(4.14) |
és az impulzus fázisának időbeli változását tartalmazó tag:
 |
(4.15) |
Láthatjuk, hogy a korábban tárgyaltak szerint ebben az esetben is a térerősség burkolója időben GD-vel tolódik el, azaz a GDD-nek az impulzus terjedési idejére nincs hatása. A (4.14)-ből adódik, hogy a GDD az impulzus időbeli kiszélesedéséért felelős. Ha a GDD olyan nagy, hogy a gyökjel alatt az 1 elhagyható, akkor kapjuk, hogy
 |
(4.16) |
azaz az impulzus időbeli kiszélesedése a GDD-vel arányos, és a bemenő impulzusidővel pedig fordítottan arányos. Ez azt a némileg meglepő eredményt adja, hogy ugyanazon GDD érték mellett egy kezdetben rövidebb impulzus nagyobb mértékben szélesedik ki, mint egy hosszabb impulzus. A (4.13) összefüggésből következik, hogy a GDD az impulzus időbeli kiszélesedése mellett a térerősség burkológörbéje maximumának csökkenését is eredményezi. Ez végülis az impulzusidő növekedéséből is sejthető, hiszen az impulzus energiája nem változhat meg. A fázis időfüggését megadó (4.15) egyenlet ( t-GD)2 tagjának együtthatójában is szerepel a GDD, azaz az impulzus csörpölődését is okozza. Tudjuk, hogy a Γ időszerinti deriváltja adja meg a pillanatnyi frekvenciát, azaz akkor pozitívan csörpölt az impulzus, ha a GDD előjele pozitív. Innen ered a csörpölés előjelének az elnevezése. A térerősség burkológörbéjének maximumámál, ahol t-GD=0, a fázis (4.15) alapján
 |
(4.17) |
A ΦCE mennyiséget vivő-burkoló fázisnak (carrier-envelope phase -CEP) nevezzük, mely megadja, hogy mennyivel tolódik el a térerősség burkológörbéje alatt a térerősség maximális értékének a helye. Ez a fizikai mennyiség, ahogy már korábban is utaltunk rá, a néhány ciklusból álló impulzusoknak az anyaggal való kölcsönhatásánál fontos szerepet tölt be. A (4.17) egyenlet megadja a kapcsolatot az időfüggő térerősség vivő-burkoló fázisa és az impulzus spektrális fázisfüggvényének együtthatói között másodrendű sorfejtés esetében. Megállapíthatjuk, hogy a vivő-burkoló fázist a spektrális fázisfüggvény mindhárom tagja befolyásolja, azonban az utolsó tag értéke maximum π/4 lehet, így általában elhagyható a többi mellett. Összefoglalva azt mondhatjuk, hogy ha az optikai elem spektrális fázisfüggvényében csak másodrendig vannak jelentős diszperziót okozó tagok, akkor a vivő-burkoló fázis értéke:
 |
(4.18) |
Az eddigi vizsgálatainknál a Φ(ω) spektrális fázisfüggvény Taylor-sorát használtuk, a sorfejtés együtthatói, azaz a fázisderiváltak tetszőleges értékűek lehettek. A következőben megvizsgáljuk konkrétan, egy L vastagságú, n(ω) törésmutatójú közeg esetében a fázisderiváltak és a törésmutató illetve deriváltjainak kapcsolatát. Ekkor a spektrális fázisfüggvény
 |
(4.19) |
alakú, ahol k a hullámszám. Tudjuk, hogy egy ω frekvenciájú monokromatikus hullám terjedési sebessége, azaz a fázissebessége
 |
(4.20) |
Korábbi tanulmányainkból ismert, hogy egy ω0 vivőfrekvenciájú hullámcsomag burkolójának csúcsa nem a fázissebességgel, hanem a
 |
(4.21) |
csoportsebességgel terjed. A (4.15) alapján az impulzus a közegből a csoportkésleltetés
 |
(4.22) |
értékével később lép ki. A spektrális fázisfüggvény deriválása után észrevehetjük, hogy a nevezőben éppen a csoportsebesség jelenik meg, azaz az L hosszúságú közegen az impulzus a vcs csoportsebességgel halad keresztül, azaz az áthaladási idő éppen a csoportkésleltetéssel egyezik meg, ahogy az a (4.15)-ből is adódott.
Ha a diszperzív közeg anyagi minőségére helyezzük a hangsúlyt, akkor célszerű bevezetni a fajlagos csoportkésleltetést (specific group delay -SGD), mely az egységnyi hosszúságú diszperzív közeg csoportkésleltetését adja meg, azaz
 |
(4.23) |
Vegyük észre, hogy az SGD a csoportsebesség reciprokával egyezik meg. Hasonló módon definiálható a fajlagos csoportkésleltetés-diszperzió (SGDD) és a fajlagos harmadrendű diszperzió (STOD) is.
Ha az impulzust nem mint különböző frekvenciájú monokromatikus hullámok, hanem mint különböző vivőfrekvenciájú hullámcsomagok összegeként fogjuk fel, akkor érdemes bevezetni a csoportsebesség-diszperzió (group velocity dispersion, GVD) fogalmát is a
 |
(4.24) |
definícióval. Vegyük észre, hogy a k hullámszám frekvenciaszerinti másodrendű deriváltja éppen az SGDD-vel egyezik meg, így a csoportsebesség-diszperzió kifejezhető az SGDD-vel is.
Ezek után tekintsünk néhány speciális esetet a fázisderiváltak hatásának szemléltetéséhez. Elsőként vizsgáljuk meg, hogy hogyan változik az impulzus térerősségének időbeli alakja, ha vákuumban L távolságot tesz meg (4.1. ábra). E célból vegyünk egy 4 fs időbeli félértékszélességű impulzust, melynek a központi vivőfrekvenciája, illetve az ennek megfelelő gyakran használt mennyiség, a központi hullámhossza 800 nm. Ez a hullámhossz a Ti:zafír lézerekkel előállított impulzusok spektrumának központi hullámhosszával egybeesik, vagy nagyon közel van hozzá.

Látható, hogy az L hossz megtételéhez a c sebességgel terjedő impulzusnak L/c idő szükséges, ami a GD-vel egyezik meg, azaz GD-vel tolódik el időben a bemenő impulzushoz képest az impulzus térerősség burkológörbéjének maximuma. Azt is láthatjuk, hogy az időbeli alakja a burkológörbének nem változik meg, így az időbeli félértékszélessége sem, azaz τ = τp0. Ezen nem lepődünk meg, hiszen a vákuum GD-nél magasabb rendű fázisderiváltjai zérusak. Ennek, valamint annak, hogy a GD·ω0 = Φ0 egy további következménye, hogy a térerősség időbeli alakja sem változik meg. Így ha kezdetben a ΦCE=0 rad, akkor L távolság megtétele után is 0 rad marad.
Ezután tekintsük azt az esetet, amikor csak a GDD értéke különbözik zérustól. Tesszük ezt azért, hogy a különböző fázisderiváltak hatásait külön-külön meg tudjuk vizsgálni. A GDD értéke legyen 40 fs2, ami kb. 2 m levegő GDD-jével egyezik meg. Az impulzus transzformlimitált időtartama ismét 4 fs.

4.2. ábra. Egy τp0 = 4 fs időbeli félértékszélességű, 800 nm-es központi hullámhosszú impulzus a) térerősségének (vastag kék vonal) és burkológörbéjének (vékony kék vonal) időbeli alakja, ha transzformlimitált, illetve GDD = 40 fs2 hatására (piros vonal).b) A két impulzus intenzitásának időbeli lefutása.
A 4.2. ábrán láthatjuk, hogy hogyan változik meg az impulzus térerőssége illetve az intenzitása pusztán csak a GDD hatására. Az impulzus, ahogy 4.14 alapján várjuk, időben jelentősen kiszélesedik, 28 fs lesz az impulzus időbeli félértékszélessége. Az időbeli megnyúlás a csúcsintenzitás drasztikus csökkenésével jár együtt. Az impulzus térerősségének periódusideje az impulzus elején hosszabb, mint a végén, azaz a pillanatnyi vivőfrekvencia az idővel nő, tehát csörpölt, méghozzá pozitívan csörpölt lett, összhangban azzal, hogy a GDD értéke is pozitív. A CEP-re vonatkozó (4.17) kifejezés kapcsán megjegyeztük, hogy a GDD csak kismértékben befolyásolja, azaz gyakran figyelmen kívül hagyhatjuk a CEP számolásakor (lásd (4.18)). A 4.2.a ábra azt mutatja, hogy valóban a GDD-nek kicsi a hatása, de nem zérus.
Csörpölt ultrarövid lézerimpulzust sem szemmel, sem fotodetektorral nem tudunk közvetlenül megfigyelni, de hanghullámokkal jól szemléltethető. Először vegyünk egy 440 Hz frekvenciájú, transzformlimitált hangimpulzust, melynek az időbeli félértékszélessége 3 s. Ekkor azt tapasztaljuk, hogy állandóan azonos a hangmagasság, csak a hang intenzitása erősödik meg, majd gyengül el. Ha pozitívan csörpölt a hangimpulzus, akkor viszont a fentiek szerint az impulzus vivőfrekvenciája az impulzus elején kisebb, mint a végén. Esetünkben ez azt jelenti, hogy kb. 20 Hz-ről 800 Hz-re nő a vivőfrekvencia, így az intenzitásváltozás mellett azt is halljuk, hogy idővel egyre magasodik az impulzus hangja. Ha negatívan csörpölt az impulzus, akkor éppen fordítva változik a vivőfrekvencia az idő függvényében, azaz kezdetben az impulzus hangja magas, majd egyre mélyebbé válik.
Következőkben tekintsük a TOD-nek a hatását, melynek értéke legyen 100 fs3 (4.3. ábra)

4.3. ábra. Egy τp0 = 4 fs időbeli félértékszélességű, 800 nm-es központi hullámhosszú impulzus a) térerősségének (vastag kék vonal) és burkológörbéjének (vékony kék vonal) időbeli alakja, ha transzformlimitált, illetve TOD = 100 fs3 hatására (piros vonal).b) A két impulzus intenzitásának időbeli lefutása.
A TOD legfontosabb jellemzője, hogy egy csökkenő mellékimpulzus-sorozatot hoz létre. Nyilván az energiamegmaradás miatt az első, főimpulzus csúcsintenzitásának csökkenie kell. A GDD-től eltérően nem okozza az impulzus időbeli hosszának jelentős megnyúlását, hiszen amint az a 4.3.b ábrán is látható, a 4 fs impulzus csupáncsak 6,6 fs-ra nyúlt meg. Viszont érdekes, hogy némileg megkéslelteti a főimpulzust, esetünkben 3,2 fs-mal. A 4.3.a ábrán látható, hogy a TOD ha kismértékben is, de megváltoztatta a CEP értékét.
Ezután térjünk rá a FOD hatásának vizsgálatára (4.4. ábra), melynek az értéke legyen 1000 fs4.

4.4. ábra. Egy τp0 = 4 fs időbeli félértékszélességű, 800 nm-es központi hullámhosszú impulzus a) térerősségének (vastag kék vonal) és burkológörbéjének (vékony kék vonal) időbeli alakja, ha transzformlimitált, illetve FOD = 1000 fs4 hatására (piros vonal).b) A két impulzus intenzitásának időbeli lefutása.
A 4.4.ábra jól mutatja a FOD jellemző hatását, azaz, hogy talpakat hoz létre az impulzus előtt és után. Az impulzusidőt relatíve nem nagyon növeli meg, esetünkben csak 8,6 fs lett (4.4.b ábra). A GDD-hez hasonlóan, amely szintén párosrendű derivált, itt is csörpöltté vált az impulzus, és a CEP-re nem volt jelentős hatása (4.4.a ábra).
Végül tekintsük az ötödrendű fázisderivált (QOD) hatását (4.5. ábra). A QOD értéke legyen 10000 fs5.

4.5. ábra. Egy τp0 = 4 fs időbeli félértékszélességű, 800 nm-es központi hullámhosszú impulzus a) térerősségének (vastag kék vonal) és burkológörbéjének (vékony kék vonal) időbeli alakja, ha transzformlimitált, illetve QOD = 10000 fs5 hatására (piros vonal).b) A két impulzus intenzitásának időbeli lefutása.
Az ötödrendű derivált esetében az látszik, hogy a hatása a harmadrendű deriválthoz hasonló, azaz ekkor is egy csökkenő intenzitású impulzussorozat alakul ki, valamint kismértékben időben eltolja a főimpulzus csúcsát. A 4.5.a ábrán látható, hogy a CEP értékét is kissé megváltoztatja.
További deriváltaknak a hatását már nem vizsgáljuk, mert egyrészt a gyakorlati esetek többségében nem jelentősek. Másrészt az eddigi példákból is láthatjuk, hogy a páros rendű deriváltakat illetően jellemző, hogy csörpöt okoznak, míg a páratlan rendűek impulzussorozatot hoznak létre. A rendszám növekedtével egyre nagyobb értékűeknek kell lenni hasonló impulzusalaktorzulás létrehozásához.
A különböző rendű fázisderiváltak hatását kipróbálhatjuk egy interaktív animáción. Az animáció futtatásához az alábbi program telepítésére van szükség.
Számolja ki, hogy 100 nm félrtékszélességű, 800 nm központi hullámhosszal rendelkező Gauss-os spektrális eloszlású impulzus mekkora transzformáció-limitált impulzusidővel rendelkezik!
Mekkorára nő egy 15 fs hosszú, transzformáció-limitált impulzus, ha 800 fs2 csoportkésés-diszperzióval rendelkező üvegtömbön halad át?
Számolja ki a BK7 típusú üveg 1 cm-re vonatkozó GD, GDD és TOD értékét 800 nm-en! A BK7-es üveg törésmutatóját megtalálja az interneten (pl. http://www.refractiveindex.info)
Fejezze ki az SGDD-t a törésmutató hullámhossz szerinti deriváltjaival!
Miért függ a transzformáció-limitált impulzusidő a spektrum alakjától?
Elérhető-e a transzformáció-limitált impulzusidő tetszőleges CEP érték mellett?
[4.1] P. Lazaridis, G. Debarge, and P. Gallion, "Time–bandwidth product of chirped sech2 pulses: application to phase–amplitude-coupling factor measurement," Optics Letters 20, 1160-1162 (1995).
[4.2] J.-C. Diels, W. Rudolph, Ultrashort Laser Pulse Phenomena, második kiadás (AP, 2006).
[4.3] J. D. Jackson, Classical Electrodynamics (Wiley & Sons, 1999).
[4.4] R. D. Guenther, Modern Optics (Wiley & Sons, 1990).
[4.5] C. Rulliere, Femtosecond Laser Pulses - Principles and Experiments, második kiadás (Springer, 2005).
[4.6] F. A. Jenkins, H. E. White, Fundamentals of Optics, hetedik kiadás (McGraw-Hill, 2001).
Tartalom
Az elemi geometriai optika egyik leglátványosabb kísérlete szivárvány színeinek előállítása a fény bontásával, melyet legegyszerűbben egy üvegprizma segítségével hozhatunk létre (5.1. ábra). A jelenség oka is jól ismert: a különböző hullámhosszúsággal rendelkező sugarak esetében a törésmutató más és más, így a Snellius-Descartes-törvény értelmében különböző szögekben törnek meg és haladnak tovább. A fény bizonyos terjedési tulajdonságai függenek a hullámhossztól, ezeket a jelenségeket összefoglaló néven diszperziónak nevezzük.

5.1. ábra. Fénytörés prizma segítségével (Forrás: [5.1])
Folytonos lézerek esetén a diszperzió hatása nem releváns, hiszen csak egy jól meghatározott hullámhosszon bocsátanak ki sugárzást. Ultrarövid impulzusüzemű lézerek esetén már nem tekinthetünk el a diszperziótól, sőt, hatása egyre jelentősebbé válik az impulzusidő csökkentésével, hiszen a Fourier-elmélet értelmében a lézersugárzás sávszélességét kell növelnünk ennek eléréséhez. A nagyobb hullámhossztartomány két végén a törésmutató egyre növekvő eltérést mutat, így az impulzus spektrumának szélein található komponensek közegbeli terjedési sebessége is különbözni fog. Ennek eredményeként a komponensek időben eltávolodnak egymástól, vagyis az impulzusidő növekedni fog. Femtoszekundumos optikában tehát kimondottan fontos az optikai elemek diszperziós tulajdonságainak ismerete.
Ahogy a 4. fejezetben is már említettük, a lineáris rendszerek elmélete sok esetben megkönnyíti a terjedés során lezajló folyamatok megértését és egyszerű matematikai alakba öntését. A törésmutató hullámhossz-, - illetve a könnyebb leírás kedvéért - frekvenciafüggésének vizsgálatához tekintsük át az egyes monokromatikus spektrális komponensek terjedési sebességét meghatározó fizikai folyamatokat.
Általános esetet tekintve, egy izotropikus, dielektromos anyagba lépő fény elektromágneses terének hatására az anyag atomjai vagy molekulái polarizálódnak, azaz a kötött elektronfelhő kissé eltávolodik az atommagtól illetve atommagoktól. Matematikai modellel ez úgy írható le, hogy az E elektromágneses térősség vektor hatására az anyagban P=ε0χE polarizációvektor lép fel, ahol ε0 a vákuum elektromos permittivitása, χ pedig az anyag elektromos szuszceptibilitása.
A monokromatikus fényhullám adott közegbeli terjedési sebességének vákuumbeli terjedési sebességéhez viszonyított arányát az n törésmutatóval jellemezzük, amely a Maxwell-egyenletek anyagbeli terjedésre vonatkozó megoldásából
 |
(5.1) |
alapján számolható. A törésmutató frekvenciafüggő viselkedésének legegyszerűbb leírását molekuláris gázok esetére a Lorentz-féle oszcillátormodell adja meg, mely a problémát egy csillapított kényszerrezgésként kezeli. A polarizált atomot vagy molekulát, mint oszcillátort gerjesztő fényt E=E0exp(iωt) elektromágneses térrel írjuk le. A σ csillapítási együtthatóval és ω0 sajátfrekvenciával rendelkező oszcillátor rezgésének viselkedése a
 |
(5.2) |
differenciálegyenlettel írható le, ahol N az m tömeggel rendelkező atomok vagy molekulák száma egységnyi térfogatban, q pedig az elektron töltése. Ennek a frekvenciafüggő χ-re kiszámolható megoldását a (5.2) összefüggésbe behelyettesítve a törésmutató frekvenciafüggése az
 |
(5.3) |
alakba írható. Az így kapott komplex törésmutató valós része az optikai törésmutató értékét adja meg, míg a képzetes rész az abszorpciót írja le. Az atomok és molekulák a valóságban egynél több abszorpciós hellyel rendelkezhetnek, amelyek azon elektronátmeneteknek felelnek meg, ahol az oszcillátor sajátfrekvenciájával rendelkező fotonok elnyelődnek. Ezeket a rezonanciacsúcsokat az úgynevezett f j oszcillátorerősségekkel jellemezve
 |
(5.4) |
formában írható le egy ritka közeg, például gáz komplex törésmutatójának frekvenciafüggése. Sűrű közegek, azaz folyadékok és szilárd testek esetén a szomszédos oszcillátorok rezgése miatt fellépő indukált térerősség miatt az (5.4) kifejezés
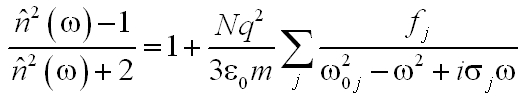 |
( 5.5) |
szerint módosul. Az 5.2. ábra egy tipikus anyag sematikus komplex törésmutatójának valós részét (azaz optikai törésmutatóját) és képzetes részét (abszorpcióját) szemlélteti.

5.2. ábra. Az abszopciós együttható és a törésmutató frekvenciafüggésének sematikus alakja
A törésmutató frekvenciafüggése az 5.2. ábrán látható módon nagyjából kétféle típusú szakaszra bontható. Az abszorpciós csúcsoktól távol eső spektrális tartományokon az anyag átlátszó, a frekvencia növekedésével a törésmutató is növekszik. A klasszikus optika terminológiája szerint, ahol törésmutató frekvencia szerinti deriváltja nullánál nagyobb, normális diszperzióval jellemzett tartománynak nevezzük. A törésmutató-görbe dn/dω < 0 tulajdonságú részein anomális diszperzióról beszélünk. A femtoszekundumos optikában azonban, az impulzusterjedés tárgyalása során sokkal nagyobb szerepe van a frekvencia szerinti második deriváltnak. Előfordulhat, hogy ebben a tudományos szakzsargonban a normális és az anomális anyagi diszperziót a d2n/dω2(vagy az ezzel szorosan összefüggő GDD)előjeléből származtatják. Gyakoribb azonban a pozitív vagy negatív diszperzió (csörp) elnevezés használata, ami némiképp egyértelműbbé teszi a kifejezések jelentését.
A normális diszperzióval rendelkező anyagok egyszerű jellemzésére szolgál az Abbé-szám. Definíciója három, látható tartományban mért törésmutató értékén alapszik, mégpedig
 |
(5.6) |
formában, ahol n d a 587,6 nm-es, n F a 486,1 nm-es és n C a 656.3 nm-es Fraunhofer-vonalnál mért törésmutató. Az Abbé-szám nagy értékei kis diszperziót takarnak, értéke tipikusan 20 (pl. sűrű flintüveg) és 60-80 (különböző típusú koronaüvegek) között változik. Az 5.3 ábrán néhány példa látható különböző üveganyagok törésmutatójának hullámhosszfüggésére a közeli ultraibolyától a látható tartományon át a közeli infravörös tartományig.

5.3. ábra. Néhány üveg törésmutatójának hullámhosszfüggése és Abbé-száma
Az impulzusterjedés és a diszperzió szempontjából csak azokat a frekvenciatartományokat érdemes megvizsgálnunk, amelyeken az abszorpció hatása elhanyagolható; itt már elegendő a komplex törésmutató valós részét alkalmaznunk. Ezeken a hullámhosszakon számos közelítő formula használata terjedt el, melyek közül a leggyakrabban a Cauchy- és a Sellmeier-típusú formalizmus szerint adják meg egy kérdéses anyag törésmutatóját. A Cauchy-formalizmus a törésmutató egyszerű ω2 szerinti Taylor-sorfejtése, de általában a
 |
(5.7) |
vákuumbeli hullámhossz szerinti alakba írva adják meg, ahol Q1, Q2, Q3 stb. anyagra jellemző állandók. Előnye a könnyű matematikai kezelhetőség, de csak szűk hullámhossztartományon ad pontos értéket. A Sellmeier-típusú formulákat ezzel szemben a Lorentz-féle oszcillátormodell abszorpciós helyektől távoli megoldására alapulva az
 |
(5.8) |
alakban adják meg. Ezen elméletileg megalapozott formula érvényessége már sokkal szélesebb hullámhossztartományra terjed ki; általánosan alkalmazható ritka közegekre, például gázokra. Szilárd testekben és folyadékokban az (5.5) egyenlet alakjában felírt Sellmeier-formulák adnak pontosabb közelítést.
A törésmutató nem csak a hullámhossztól függhet, hanem az anyag állapotjelzőitől is. Gázok esetén igen jelentős különbségek fordulhatnak elő a törésmutatóban a hőmérséklet és nyomás változása miatt, gondoljunk csak a légköri fényjelenségekre. Ennek leírására a Lorentz-Lorenz-elmélet kínál megoldást. A T hőmérsékletű, p nyomású, Z kompresszibilitással rendelkező, ρ sűrűségű gázkeverék törésmutatójára az
 |
(5.9) |
összefüggés írható fel, ahol R az univerzális gázállandó, az A m (ω) az x m móltörttel és M m moláris tömeggel rendelkező m-edik gázkomponens molekuláris polarizálhatósága, az
 |
(5.10) |
pedig a Lorentz-Lorenz-paraméter.
Mivel extrém esetektől eltekintve a gázok törésmutatója 1-hez igen közel van, alkalmazhatjuk az
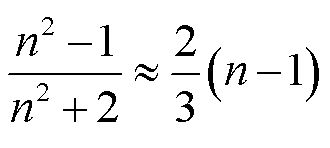 |
(5.11) |
közelítést. Felhasználva azt, hogy az ideális gázok kompresszibilitása Z = 1, az (5.9) egyenlet gázkeverékekre vonatkozó alakját felírhatjuk az egyszerűbb
 |
(5.12) |
formában, ahol - emlékeztetőül - x m a móltörtet, A m (ω) a molekuláris polarizálhatóságot jelenti, míg R az univerzális gázállandó, és p, illetve T a gáz nyomása és hőmérséklete. A fajlagos fázisderiváltak pedig az
 |
(5.13) |
 |
(5.14) |
 |
(5.15) |
alakban fejezhetők ki. Ezek alapján megállapíthatjuk, hogy a fázisderiváltak lineáris kapcsolatban állnak a gázkeverék össznyomásával. Amennyiben a gázkeverék összetevői nem lépnek kémiai reakcióba egymással, alkalmazhatjuk Dalton törvényét. A teljes gázkeverékre vonatkozó törésmutató és fázisderiváltak felírhatóak az egyes összetevők parciális nyomásával számolt törésmutatók és a megfelelő fázisderiváltak összegeként. Ha a keverék N-féle, megkülönböztethető gázt tartalmaz, melyek közül az m-edik gáz parciális nyomása pm, akkor az
 |
(5.16) |
 |
(5.17) |
 |
(5.18) |
 |
(5.19) |
kifejezéseket alkalmazhatjuk gázkeverékek spektrális fázisának számolásakor.
Az optikai szálak igen fontos szerepet töltenek be az optikai jelek vezetésében, hiszen a szabad térben való terjedéssel szemben mechanikailag sokkal rugalmasabban irányítható, nincs szükség tükrökre, nem lépnek fel nyalábstabilitással, divergenciával kapcsolatos problémák. A fénynyaláb megőrzi tulajdonságait több száz kilométernyi terjedés során is, amivel légköri körülmények között igen nehéz lenne felvenni a versenyt. Az optikai szálakban való terjedés során azonban más jellegű nehézségek lépnek fel, melyek megnehezítik az optikai jelek átvitelét. Az anyagi diszperzió mellett fellép az úgynevezett módusdiszperzió is, amennyiben a hullámvezetőben több módusban terjedhet a fény. Ez azt jelenti, hogy a különböző optikai úthosszakat befutó módusok között úgynevezett differenciális móduskésés lép fel, mely jelentősen függ a szál mag körüli törésmutatóprofiljától. A módusdiszpezió erősen limitálja az adatátviteli sebességet, hiszen nem használható tetszőlegesen rövid impulzus a szálban, mert az jelentősen meghosszabbodna a terjedés során. Az effektus hatása minimalizálható parabolikus törésmutatóprofillal, illetve egymódusú szál alkalmazásával.

5.4. ábra. Fotonikus szál keresztmetszetének elektronmikroszkópos felvétele. (Forrás: [5.2]).
Az ultrarövid impulzusok vezetésére az úgynevezett üreges maggal és azt körülvevő mikrostruktúrált köpennyel rendelkező, fotonikus kristályból létrehozott szálak (az angol nyelvű irodalomban a hollow-core fiber, a photonic crystal fiber és a microstructure fiber elnevezések egyaránt elterjedtek) alkalmasak, amelyek speciális tulajdonsága, hogy a vezetett fény csupán töredéke terjed a szál anyagában. A szál hullámvezetési tulajdonságait így túlnyomórészt az apró, egymáshoz nagyon közeli légcsatornák határozzák meg, amelyek a szál teljes hosszán végigfutnak. A lyukak elrendezésével, méretével és formájával rendkívül széles tartományon érhetőek el különleges és egymástól nagyon eltérő tulajdonságok, amelyek sokrétű felhasználást tesznek lehetővé. Alkalmazható például az impulzus sávszélességének kiszélesítésére, azaz szuperkontinuum keltésére. Diszperziós tulajdonságai is kiválóan alakíthatóak, negatív diszperzió is könnyen létrehozható benne, így elterjedten alkalmazzák szállézerek erősítőiben az impulzusok időbeli összenyomására is.
Az anyagi diszperziónak nem csupán a transzmissziós optikai elemeken történő áthaladáskor van hatása a rövid impulzusokra, hanem legtöbbször reflexiós esetben is. Elemi optikából jól ismert, hogy a reflexiós együtthatót a fény polarizációja és beesési szöge mellett az anyag törésmutatója is befolyásolja. Amennyiben az impulzus egyetlen felületről verődik vissza, a spektrális fázis nem szenved változást. Ha azonban a felületre több, különböző vastagságú és eltérő törésmutatóval rendelkező vékonyréteget viszünk fel, akkor annak már komoly hatása lehet az egyes felületekről részleges visszavert fényből összeálló impulzus spektrális fázisára éppúgy, mint egyéb más tulajdonságaira. Az ilyen típusú optikai elemeket dielektrikum-tükröknek nevezzük. Jellemző rájuk, hogy speciális, előre megtervezhető reflexiós és diszperziós tulajdonsággal rendelkeznek, de ezek a paraméterek igen érzékenyek a megadott hullámhossz-tartományra, polarizációra és beesési szögre.
A Gires-Tournois-interferométer az egyik legegyszerűbb példa arra, hogy hogyan hozható létre negatív diszperzióval rendelkező reflexiós optikai elem. Az eszköz tulajdonképpen egy állóhullám-rezonátor, mely sok hasonlóságot mutat a Fabry-Perot-interferométerrel. Két reflexiós felületből áll, melyből az első részlegesen visszaverő tulajdonsággal rendelkezik (R1), míg az ettől d távolságra elhelyezkedő másodikon teljes visszaverődés megy végbe (lásd 5.5 ábra). Ha feltételezzük, hogy a rezonátor veszteségmentes, akkor a teljesítmény-átvitel minden hullámhosszon azonos, 100%. A csoportkésés spektrális függése azonban periodikus jelleget mutat és bizonyos frekvenciákon csúcsokkal rendelkezik. A csúcs annál élesebb, minél nagyobb az első felület reflexiós együtthatója, a csúcsok távolsága pedig a d paramétertől és a felületek közötti anyag törésmutatójától függ.

5.5. ábra. A Gires-Tournois interferométer vázlatos rajza
Érdemes megjegyezni, hogy az eszköz által létrehozni kívánt hatás létrehozható attól függetlenül, hogy milyen törésmutatóval rendelkező anyag van a felületek között. Természetesen a fázisderiváltak is követik a periodikus jelleget, a GDD ott vált előjelet, ahol a rezonancia-csúcs és két csúcs közötti minimum van a csoportkésés spektrális függvényében (lásd 5.6. ábra). Azokon a tartományokon ahol a GDD negatív, ott az eszköz hatékonyan alkalmazható impulzusok kompresszálására. A GDD mértéke hangolhatóvá tehető, amennyiben a két felület távolsága nem rögzített.

5.6. ábra. A Gires-Tournois interferométer által létrehozott GDD-változás spektrális függése (Forrás: [5.3]).
A Gires-Tournois-interferométer gyakorlati megvalósításával azonban stabilitási problémák léphetnek fel. Egy hordozóra párologtatott rétegek alkalmazásával sokkal stabilabb hatás érhető el, de ehhez fel kell áldoznunk a hangolhatóságot.
Két különböző törésmutatóval rendelkező anyagból felváltva felépített rétegek sorozatát nevezzük Bragg-tükörnek, vagy elosztott Bragg-reflektorak. Leggyakrabban a negyedhullám-tükör változatát alkalmazzák, amelyben az optikai rétegek vastagsága - az alkalmazott beesési szöget figyelembe véve - a tervezett optikai hullámhossz negyedének felelnek meg. A rétegek közötti határfelületeken a Fresnel-egyenleteknek megfelelően oszlik el a beeső fény intenzitása és iránya. Az 5.7. ábra szemlélteti a Bragg-tükörre eső fény behatolási mélységét különböző hullámhosszakon.

5.7. ábra. A Bragg-tükör törésmutató-profilja (fekete görbe), valamint a fény behatolási mélysége a tervezési (1000 nm, kék görbe), illetve attól eltérő (800 nm, szürke görbe) hullámhosszon. A 800 nm-es hullámhosszal rendelkező fény nagy része áthatol a rétegeken, 1000 nm-en azonban erős reflexiót kapunk. (Forrás: [5.3])
Két azonos anyagú rétegről történő visszaverődés közötti optikai úthossz a hullámhossz felének felel meg, így a visszavert komponensek egymást erősítő interferenciát hoznak létre. Ennek eredményként egy magas reflexióval rendelkező felületet kapunk. Az elért reflexiós együtthatót az alkalmazott rétegek száma és a két anyag törésmutató-kontrasztja határozza meg; míg a sávszélesség főként csak az utóbbi függvénye.

5.8. ábra. A visszaverőképesség (fekete görbe, bal oldali skála) és a GDD (kék görbe, jobb oldali skála) a hullámhossz függvényében egy 1000 nm-re tervezett Bragg-tükör esetében. (Forrás: [5.3])
A Bragg-tükrök esetében a diszperzió jelenlétével is számolni kell. Az 5.8. ábra szemlélteti a reflexiós együttható és a csoportkésés-diszperzió spektrális változását. Míg igen széles tartományon magas reflexió érhető el, a csoportkésés-diszperzió a tervezési hullámhossz környékén még kicsi, de attól távolodva abszolút értéke gyorsan növekszik.
A Bragg-tükörből kiindulva, általánosabb értelemben a több, különböző anyagú, átlátszó optikai vékonyrétegből álló tükröket dielektrikum-tükröknek nevezzük. A rétegek megfelelő kombinálásával sokféle reflexiós, polarizációs és diszperziós tulajdonság szinte tetszőlegesen kialakítható, valamint a sávszélesség is jól előre tervezhető. Éles spektrális levágással rendelkező élszűrő, felül- vagy aluláteresztő és sávszűrő optikai elemek is létrehozhatóak ezzel a módszerrel.
A réteg-rendszer működésének tulajdonságai nem csak egy hullámhosszra tervezhetőek, például kialakítható olyan tükör, amely (két vagy több) különböző hullámhosszon rendelkezik speciális tulajdonsággal, például olyan esetben, ha valamely fényjel keltése esetén nagyon eltérő hullámhosszúságú pumpanyaláb is jelen van, így ilyenkor vagy mindkét hullámhosszra magas reflexió, vagy egyik nyaláb esetében magas reflexió, míg másik nyaláb esetében magas transzmisszió kívánatos. Az ilyen tükröket dikroikus tükröknek nevezzük.
A polarizációs tulajdonságok tervezésével előállíthatóak olyan optikai elemek, melyek vékonyréteg-polarizátorként, polarizációs, - vagy éppen ellenkezőleg - nem polarizáló nyalábosztóként viselkednek.
A dielektrikum réteget mindkét polarizációs síkra lehet tervezni és görbült felületekre, azaz fókuszáló illetve defókuszáló tükrökre is fel lehet párologtatni. Ilyen esetekben is figyelembe kell venni a beesési szögeket, azaz előfordulhat, hogy a gömbtükör fókuszáláson és kollimáláson kívül más leképzési műveletre nem alkalmas. Kis sugarak esetén (pl. 10 mm alatt) a homogenitás és a stabilitás tekintetében számítani lehet a felület minőségének gyengülésére.
Mivel a dielektrikum-tükrök gyakran olyan hullámhosszra készülnek, amelyek a látható tartományon kívül esnek, első pillantásra sokuk nem is tűnik tükörnek, hiszen ilyen esetben gyakorlatilag átlátszó. Fény felé fordítva és a beesési szöget változtatva különböző színű lehet, és néhány esetben nagyon nehéz megmondani, hogy a tükör hordozójának melyik oldalán van a bevonat.
A dielektrikum tükröknek azt a típusát, amelyekkel az ultrarövid lézerimpulzusok diszperziója passzív módon szabályozható, csörpölt tükröknek nevezzük [5.4]. Legtöbb esetben negatív diszperzióval rendelkeznek, hiszen a különböző közegekben történő terjedés során jelentős mennyiségű pozitív diszperzióval terhelődhet az impulzusok spektrális fázisa, ezek kompenzálására szolgálnak ezek az eszközök. Alapvetően abban különböznek a Bragg-tükröktől, hogy a rétegek vastagsága nem állandó, hanem megfelelően változik, így a különböző hullámhosszal rendelkező spektrális komponensek más-más mélységig hatolnak be, így eltérő csoportkésést szenvednek, amint ez az 5.9. ábrán is látható.

5.9. ábra. A rétegstruktúrába behatolt elektromos tér intenzitása a hullámhossz és a behatolási mélység függvényében. (Forrás: [5.3])
A valóságban a rétegszerkezet kicsit összetettebb, egyébként erős oszcillációk jelennének meg a GDD spektrális függésében; de numerikus optimalizálás segítségével megtervezhető a kívánt tulajdonsággal rendelkező rétegszerkezet. Az 5.10. ábra egy csörpölt tükör reflexiós és diszperziós tulajdonságait szemlélteti.
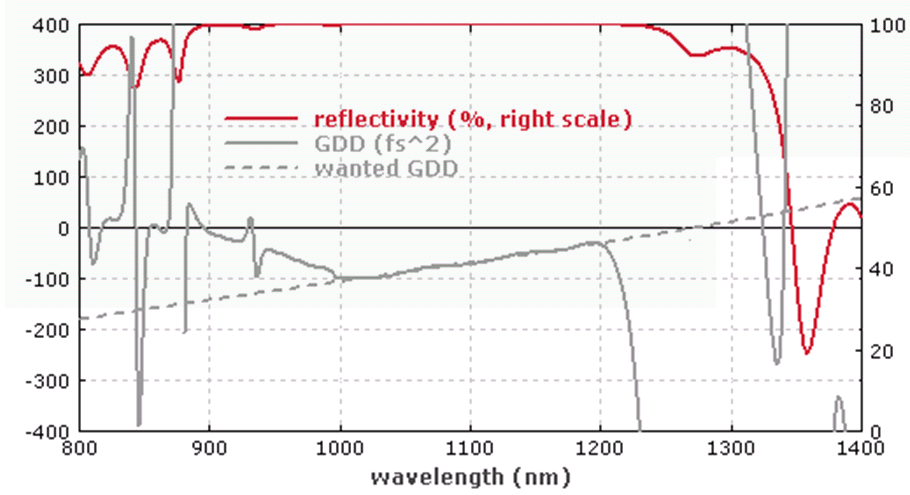
5.10. ábra. Egy csörpölt tükör tipikus reflektivitás- (vörös görbe) és diszperzió-profilja (szürke görbe) a hullámhossz függvényében. (Forrás: [5.3])
A csörpölt tükrök egyik legfontosabb alkalmazása az ultramagas sávszélességgel rendelkező, néhány ciklusú impulzusok előállításához kapcsolódik. Az ilyen impulzusokat előállító módusszinkronizált lézeroszcillátorokban a diszperzió kompenzálása és szabályozása kulcsfontosságú szerepet játszik. Mivel egyetlen csörpölt tükörrel csak korlátozott mennyiségű diszperzió kompenzálására van lehetőség, így több tükör együttes hatását használják. Sok esetben nem csak a csoportkésés-diszperzió kompenzálását végzik el, hanem a magasabb rendű diszperziós együtthatókat is figyelembe veszik.
Hogyan módosul a normális és anomális diszperzió definíciója, ha a törésmutató hullámhossz szerinti deriváltjával fogalmazzuk meg?
Mi a fizikai jelentése a gázkeverék fajlagos csoportkésését kifejező (5.13) egyenletben a 1/c konstansnak?
Hogyan folytatódna az (5.13)-(5.15) sor a fajlagos negyedrendű diszperzióra vonatkozó kifejezéssel?
Optikai szálakban mit nevezünk a módusdiszperziónak és miért jön létre?
Létrehozható-e pozitív diszperzióval rendelkező Gires-Tournois-interferométer?
Hogyan változna a Gires-Tournois-interferométer GDD-je, ha a részlegesen átersztő felület reflexióját változtatni tudnánk?
Okoz-e csoportkésést egy nulla GDD-vel rendelkező Bragg-tükör, és kell-e ezt kompenzálni?
Mik az előnyei és hátrányai a dielektrikum-tükröknek a fémtükrökkel szemben?
Mi történne, ha néhány ciklusú impulzusok terelésére nem megfelelően nagy sávszélességű dielektrikum-tükröket használnánk?
Miért nem lehet tetszőlegesen nagy GDD-t létrehozni egyetlen csörpölt tükör segítségével?
[5.1] Adam Hart-Davis, http://scienceblogs.com/startswithabang/files/2012/08/prism-and-refraction-of-light-into-rainbow-AJHD.jpeg
[5.2] NKT Photonics A/S, http://www.nktphotonics.com
[5.3] RP Photonics, http://www.rp-photonics.com/
[5.4] R. Szipőcs, K. Ferencz, C. Spielmann, F. Krausz, "Chirped multilayer coatings for broadband dispersion control in femtosecond lasers," Optics Letters 19, 201-203 (1994).
Tartalom
A széles spektrummal rendelkező fénynyalábok különböző hullámhosszúságú komponensei nem csak különböző terjedési sebességgel rendelkezhetnek, de terjedési irányaik is eltérőek lehet, ebben az esetben beszélünk szögdiszperzióról. Ilyen jelenség például akkor jön létre, ha a szélessávú fénynyaláb eltérő diszperzióval rendelkező anyagok közötti felületen megtörik, prizmán halad át, vagy rácson szenved elhajlást.
A szögdiszperziónak kétféle definíciója is használatos. A geometriai optika felől megközelítve, ha a spektrális komponensek terjedési irányának hullámhosszfüggéséről beszélünk, akkor azt γTIterjedésiirány-szögdiszperziónak nevezzük (lásd pl. [6.1]). Egy másik, valamivel általánosabb hullámoptikai meghatározás alapján az adott hullámhosszakhoz tartozó virtuális hullámfrontok által bezárt szög hullámhosszfüggését jellemezzük az úgynevezett γFF fázisfront-szögdiszperzióval (lásd pl.[6.2]). A kétféle definíció alapján bevezetett mennyiségek síkhullám-közelítésben azonos viselkedést írnak le; de más esetekben, például Gauss-nyalábok tárgyalásánál már különbözőképpen fejlődnek a terjedés során. A 6.1. ábra hasonlítja össze ezt a két esetet.

6.1. ábra. A kétféle módon értelmezett szögdiszperzió összehasonlítása síkhullám (a), illetve Gauss-nyaláb (b) közelítésben
Míg a γTI terjedésiirány-szögdiszperzió - szabad terjedés esetén - végig állandó marad, a nyalábnyakban a vele megegyező γFF fázisfront-szögdiszperzió az optikai tengely mentén a görbületi sugár folyamatos növekedése (ezzel együtt a virtuális hullámfrontok által bezárt szögek csökkenése) miatt csökken, a Rayleigh-hossznál már csupán feleakkora értékű, és aszimptotikusan nullához tart. A görbületi sugarak hullámhosszfüggése miatt az optikai tengelytől távolodva, lineárisan növekvő, másodrendű szögdiszperzió jelenik meg. A fázisfront-szögdiszperzió fejődését a nyalábnyaktól az optikai tengelyen z távolságra, az optikai tengelytől r távolságra, λ hullámhosszon a
 |
(6.1) |
közelítő kifejezés írja le, ahol w0 a nyalábnyak mérete.
Széles spektrális tartománnyal rendelkező fény terjedésekor minden esetben számolni kell a szögdiszperzió jelenségével, akár folytonos, akár impulzus jellegű sugárzásról legyen szó. Míg a folytonos fény és hosszú lefutású impulzusok esetében kevésbé, ultrarövid hullámcsomagok esetében már sokkal inkább kiemelt szerepe van a tér-időbeli eloszlásnak. Ennek megfelelően, ultrarövid impulzusok esetén a szögdiszperzió jelentős időbeli kiszélesedést okoz akkor is, ha a közeg nem, vagy csak elhanyagolható mértékű anyagi diszperzióval rendelkezik.
A szögdiszperzió vákuumban terjedő ultrarövid impulzusra kifejtett hatását a 6.2. ábra szemlélteti. A kiinduló impulzus spektrális összetevői térben és időben átfednek, de a szögdiszperzió miatt terjedési irányuk kissé eltér egymástól. A vákuumban (valamint izotróp anyagban) terjedő hullámok terjedésiirány-szögdiszperziója a terjedés közben állandó marad, de az impulzusra kifejtett hatása a megtett út növekedésével egyre jelentősebb.

6.2. ábra. Egy ultrarövid impulzus szögdiszperzió miatt kialakult tipikus térbeli alakja bizonyos távolság megtétele után
A 6.2. ábrán az impulzus spektrális komponenseinek térbeli intenzitáseloszlását látjuk valamekkora z távolság megtétele után. Szögdiszperzió jelenléte esetén a terjedésre merőleges x irányban az impulzus középpontjától távolodva az impulzusidő növekszik, és a spektrális komponensek szeparálódása miatt - a spektrum csúcsa is eltolódik az impulzus különböző oldalain. Az optikai tengelyen (x=0-nál) sem marad meg az eredeti impulzusidő, ugyanis könnyen belátható, hogy egy τ0 transzformlimitált időbeli félértékszélességgel rendelkező impulzus
 |
(6.2) |
csoportkésleltetés-diszperziónak megfelelő fázistorzulást szenved. Gauss-os impulzusalak esetén a jól ismert
 |
(6.3) |
összefüggést használva közelíthető a kialakult impulzus hossza.

6.3. ábra. Az impulzusidő kiszélesedése különböző terjedési távolságok esetén a szögdiszperzió függvényében (a), illetve az időbeli kontraszt alakulása Gauss-os, illetve kvadratikus hiperbolikus szekáns alakú impulzusalak esetén 5 fs-os transzfomlimitált impulzusidőből kiindulva [6.3].
A fenti összefüggéseket alapul véve, a 6.3.a ábra egy numerikus példával demonstrálja az említett jelenséget: egy 5 fs-os, transzformlimitált impulzusidejű, Gauss-os jellegű hullámcsomag kiszélesedését követhetjük nyomon a szögdiszperzió függvényében különböző terjedési úthosszak esetén. A 6.3.b ábrán az időbeli kontraszt alakulásából azt a tanulságot vonhatjuk le, hogy a szögdiszperzió növekedésével az impulzus csúcsa egyre inkább elmosódik, a hordozott energia egyre inkább szétoszlik, ami a kompresszor után már igen nehezen kompenzálható.
A (6.3) összefüggés csak akkor érvényes, ha a sávszélesség viszonylag keskeny, a transzformlimitált impulzusidő 30-50 fs felett van. Ez alatt a magasabb rendű, de legalább a harmadrendű diszperziót is figyelembe kell vennünk az időbeli alak megfelelő pontosságú számolásához. Abban az esetben, ha a szögdiszperzió spektrális függése lineáris jellegű (azaz dθ/dλ>>λ0·d2θ/dλ2), akkor élhetünk a
 |
(6.4) |
közelítéssel. Az időbeli hosszra a harmadrendű diszperzió akkor lesz hatással, ha a TOD SZD ·Δω szorzat azonos nagyságrendbe esik a GDD-vel. Ha még nagyobb a TOD aránya, akkor az az impulzus időbeli alakjában kisebb mellékcsúcsok jelennek meg, melyek a TOD abszolútértékének növekedésével egyre jelentősebbé válnak, és még tovább rontják az időbeli kontraszt értékékét.
Annak eredményeképpen, hogy az ultrarövid impulzusok térbeli hossza a terjedési irány mentén rövidebb, de legalábbis összemérhető a terjedési irányra merőleges kiterjedésével, a prizmán való törés, rácson való elhajlás, stb. a szögdiszperzió keletkezése mellett további, nem kívánt impulzus-deformációkat okozhat. Egyik ilyen jelenség az impulzusfront dőlése, melyet sematikusan a 6.4 ábra szemléltet.
A szögdiszperzió gyakorlatilag minden esetben együtt jár az impulzusfrontdőlés jelenségével, ha véges kiterjedésű nyalábot vizsgálunk. Ha az impulzusfront szögben érkezik, illetve hagyja el a prizma felületeit, vagy a rács felszínét, az impulzus két oldala különböző úthosszakat fog bejárni, emiatt az impulzusfront két széle között csoportkésés jelenik meg, vagyis a terjedési irányhoz képest megdől.

6.4. ábra. Az impulzusfront-dőlés szemléletes bemutatása. (Forrás: [6.4])
Könnyen belátható, hogy egységnyi keresztmetszetre nézve a csoportkésés mértéke
 |
(6.5) |
ami a hullámcsomag további, a szögdiszperzió hatásán felüli időbeli hosszabbodását is eredményezni. A dőlt impulzusfront általános esetben a terjedésre merőleges iránnyal
 |
(6.6) |
szöget zár be.
Azt a jelenséget, amikor a nyaláb keresztmetszete mentén változik az impulzus spektrális összetétele, térbeli csörpnek szokás nevezni. Az effektus szintén természetes velejárója a szögdiszperziónak, ahogyan a 6.2. ábrán is látható, a nyaláb egyik oldala a vörös irányba tolódik el, míg a másik oldalán a kék színű komponensek a dominánsak.

6.5. ábra. Térbeli csörp kialakulása plánparalel lemezen, szögben történő áthaladáskor (a), valamint prizmapár kétpasszos elrendezésben a szögdiszperzió és a térbeli csörp együttes kompenzálása végett (b). (Forrás: [6.5])
A szögdiszperzió kompenzálása azonban általában nem jár együtt a térbeli csörp megszüntetésével, valamint a spektrum térbeli modulációját okozza az egyszerű plánparalel lemezen szög alatt történő áthaladás is (lásd 6.5.a ábra). A teljes, szögdiszperzióra és térbeli csörpre vonatkozó kompenzálás érdekében alkalmaznak kétpasszos elrendezést prizma- és rácspárok esetén, például ahogy ez a 6.5.b. ábrán is látható.
A térbeli csörp is legalább kétféleképpen értelmezhető és mérhető a nyalábprofil térbeli-spektrális felbontásának diagramján. Egyrészt ha a diagram spektrális metszeteit vesszük adott pozícióknál és ehhez rendeljük hozzá a spektrum csúcsértékét, az így kapott görbe meredeksége ad egy úgynevezett frekvencia-gradienst, amely jól jellemzi a térbeli csörpöt. A másik megközelítési módban egy adott hullámhossznál vett metszet ad egy intenzitáseloszlást, amely csúcsértékének pozícióját rendeljük hozzá a vonatkozó hullámhosszértékhez. Ennek első deriváltja adja a térbeli diszperziót, amely szintén szoros összefüggésben van a térbeli csörppel. A kétféle definíció összehasonlítását a 6.6. ábra szemlélteti. X. Gu és munkatársai ([6.5]) analitikusan bebizonyították, hogy Gauss-os alakú nyalábprofil és spektrum esetén a két megközelítés azonos módon alkalmas nem túlságosan nagy térbeli csörp jellemzésére.

6.6. ábra. A térbeli diszperzió és a frekvencia-gradiens összehasonlítása egy nyaláb spektrálisan és térben bontott diagramján. (Forrás: [6.5])
Folytonos fénynyaláb esetén beszélhetünk-e szögdiszperzióról?
Lehet-e értelmezni Gauss-nyalábok esetén a terjedésiirány-szögdiszperziót a Rayleigh-hossznál?
Számolja ki egy egyenlő oldalú, BK7 anyagú prizma által keltett szögdiszperziót 800 nm-en, minimális deviáció esetén!
Függ-e pl. egy prizma által létrehozott szögdiszperzió értéke a bemeneti impulzus GDD-jétől?
Számolja ki egy egyenlő oldalú, BK7 anyagú prizma által keltett inpulzusfrontdőlés szögét 800 nm-en, minimális deviáció esetén!
Keletkezik-e térbeli csörp, ha szélessávú impulzusok két, egymással szembefordított, párhuzamos felületű, megegyező diffrakciós síkkal rendelkező rács felületén diffraktálódnak?
[6.1] F. A. Jenkins, H. E. White, Fundamentals of Optics, hetedik kiadás (McGraw-Hill, 2001).
[6.2] M. Born, E. Wolf, Principles of Optics, hetedik kiadás (Cambridge, 1999).
[6.3] K. Osvay, A. P. Kovács, Z. Heiner, G. Kurdi, J. Klebniczki, M. Csatári, "Angular dispersion and temporal change of femtosecond pulses from misaligned pulse compressors," IEEE Journal of Selected Topics in Quantum Electronics 10, 213-220 (2004).
[6.4] G. Pretzler, A. Kasper, K. J. Witte, "Angular chirp and tilted light pulses in CPA lasers," Applied Physics B 70, 1-9 (2000).
[6.5] X. Gu, S. Akturk, R. Trebino, "Spatial chirp in ultrafast optics," Opt. Commun. 242, 599-604 (2004).
Tartalom
Az ultrarövid impulzusok egyik legelőnyösebb tulajdonsága az, hogy időbeli hosszúságuk egyszerű optikai eszközök segítségével könnyen alakítható mindkét irányban, azaz nemcsak az impulzushossz növelésére van lehetőség, hanem annak csökkentésére is. Ha az impulzust egymáshoz közeli frekvenciával rendelkező hullámok szuperpozíciójaként képzeljük el, melyek egy pontban mind erősítik egymást (ez felel meg az impulzus csúcsának), akkor könnyen megérthető az impulzusidő alakításának mechanizmusa: a hullámok fázisának egymáshoz képesti eltolása rontja az adott pontbeli szuperpozíciót, így növekszik az impulzusidő; illetve minél jobban összehangoljuk a fázisokat, annál rövidebb impulzust kapunk. Egy adott spektrális összetételű impulzus időbeli alakja természetesen nem rövidíthető tetszőlegesen. Azt a minimális időtartamot, amelynél tovább nem lehet rövidíteni a hullámcsomag időbeli hosszát, vagyis amikor előáll az az eset, hogy minden spektrális hullámkomponens fázisa megegyezik, transzformlimitált impulzusidőnek nevezzük.
Akkor érhetünk el tehát rövid impulzusidőt, ha minél szélesebb tartományon igazítjuk össze a komponensek fázisát, azaz a spektrális fázis, pontosabban ennek deriváltja, a diszperzió megfelelő alakítására van szükség. Ez már a néhány femtoszekundumos impulzusok előállításánál is nélkülözhetetlen: egy lézeroszcillátort akkor tudunk széles sávban, impulzus-üzemmódban működtetni, ha a körüljárási idő minden spektrális komponensre azonos, más szóval az optikai úthosszak különböző hullámhosszakon is megegyeznek. Ebben az esetben a titán-zafír alapú aktív közeg nem csak egyetlen hullámhosszat (folytonos lézer-üzemmód) tud erősíteni, hanem a különböző hullámhosszú, spektrális komponensek egész sorozatát. Ha ez a feltétel fennáll, és egy külső mechanikai zavar hatására valamely pillanatban a fázisok is konstruktív szuperpozíciót hoznak létre, az elért nagy intenzitás hatására önstabilizáló nemlineáris folyamat, az úgynevezett Kerr-lencsés módusszinkronizáció indul be, és ezzel az ultrarövid impulzussorozat előállítása önfenntartóvá válik. A Kerr-lencsés módszer mellett számos más eljárás is használatos a módusszinkronizáció beindításásra, azonban az ultrarövid impulzusok titán-zafír kristállyal történő előállításához messze ez bizonyult eddig a legsikeresebbnek.
Ha az oszcillátor olyan diszperziókompenzálása széles spektrális tartományon működik, hogy a keltett transzformlimitált impulzusok már csak néhány optikai ciklusból állnak, akkor a legtöbb kísérlet szempontjából már igen fontos a CEP állandó értéken tartása. Mivel a legkisebb mechanikai zavar és hőmérsékletváltozás megváltoztatja az oszcillátor optikai úthosszát, stabilizálás nélkül a különböző CEP értékkel rendelkező impulzusok más és más hullámalakkal rendelkeznek, így a kísérletek kimenetele sem lesz azonos. A egyik legelterjedtebb módszer a CEP impulzusról impulzusra történő változásának, azaz a CEP csúszásának mérésére az ún. f-to-2f interferometria [7.1]. A oszcillátor stabilizálása megoldható azáltal, hogyha a mért jelet megfelelő módon visszacsatoljuk az oszcillátorba, leggyakrabban a pumpa teljesítményének, a kristály hőmérsékletének vagy például az optikai útba helyezett ékpár mozgatásának segítségével.
A diszperzió manipulálása nem csak az ultrarövid impulzusok előállításánál játszik döntő szerepet, hanem azok erősítésénél is. A módusszinkronizált oszcillátorban stabilitási okok miatt nem állítható elő tetszőlegesen nagy térerősségű impulzus, de a rezonátoron kívül, további, például megfelelően pumpált titán-zafír kristállyal az impulzusok energiája sokszorosára növelhető. Direkt erősítés alkalmazásával a folyamat idő előtt telítésbe megy, illetve egyes optikai elemek roncsolódhatnak. D. Strickland és G. Mourou ismerték fel, hogy az impulzusok időbeli nyújtásával a magimpulzusok csúcsintenzitása is reverzibilis módon csökkenthető, így az erősítés is sokkal hatékonyabban végezhető. Ezt az eljárást fázismodulált impulzuserősítésnek (chirped-pulse amplification - CPA) nevezik [7.2].
Egy CPA-rendszer legtöbb esetben három fő szakaszból áll, melyeket a 7.1 ábra folyamatábrája szemlélteti. A módusszinkronizált oszcillátort elhagyó, nJ nagyságrendű impulzusenergiával és közel transzformlimitált időbeli alakkal rendelkező magimpulzusok először az impulzusnyújtón (stretcher) haladnak végig, amelyben az egyes spektrális komponensek különböző úthosszakat futnak be, ezáltal az impulzusok időben több nagyságrenddel is megnyúlnak. Az impulzusidő hosszabbodása a térerősség és ezen keresztül az intenzitás maximumának csökkenéséhez vezet; így a megfelelő mértékben csökkentett intenzitású impulzusok erősítése optikai roncsolódás nélkül végezhető, egészen az erősítő közeg telítődéséig.

7.1. ábra. Femtoszekundumos impulzusok erősítésére szolgáló fázismodulált impulzuserősítő (CPA) rendszer sematikus felépítése.
Az erősítési szakasz (amplifier stage) (lásd animáció) során legtöbb esetben szilárdtest alapú erősítőközeget gerjesztünk egy nagy energiájú pumpalézer segítségével, mely az energiát a kristályon egymás után többször keresztülhaladó nyújtott impulzusnak adja át, áthaladásonként a telítéstől függően általában 1,1-10-szeresére növelve annak energiáját. Az erősítés egyik legjelentősebb hátráltató tényezője az erősítőközegben kialakuló erősített spontán emisszió (amplified spontaneous emission -ASE), melyet az erősítő szakaszok tervezésénél figyelembe kell venni. Összességében egy vagy akár több erősítési szakasz alkalmazásával a nyújtott impulzusok energiája 6-9 nagyságrenddel növelhető.
Egy igen elterjedt alternatív erősítési eljárás az optikai parametrikus fázismodulált impulzuserősítés (optical parametric chirped pulse amplification - OPCPA [7.3]) mely során a ns körüli időtartamra nyújtott magimpulzusokat χ(2) típusú nemlineáris kristály segítségével erősítjük. Ennek a módszernek az egyik előnye az, hogy már egyszeri áthaladás is elegendő a megfelelő erősítés eléréséhez, így elkerülhetőek a bonyolult, többszöri áthaladást igénylő rendszerek, és egyszerűbb, helytakarékosabb kivitelben megvalósítható. Ennek következtében az erősített impulzusok nyalábprofiljának minősége és időbeli kontrasztja, vagyis az impulzus csúcsintenzitásának és a háttérzaj intenzitásának aránya nagymértékben javítható. További érv az OPCPA mellett, hogy az erősítési spektrum igen széles tartományt ölel át; ugyanakkor nehézséget jelentenek a fázisillesztéssel és a pumpaimpulzusok szinkronizálásával kapcsolatos problémák.
Az optikai erősítés után, a CPA-rendszerek utolsó szakaszában az impulzusok időbeli összenyomását kell végrehajtani, erre szolgál az impulzusösszenyomó vagy kompresszor (compressor). Feladata alapvetően tehát ellentétes az impulzusnyújtóéval: a teljes rendszer spektrális fázistolását nullára kell visszaállítania. Emellett a nyaláb minőségének, az impulzusok térbeli és időbeli alakjának megőrzésére is alkalmasnak kell lennie, ami igen összetett feladat.
Az időben megnyújott illetve össszenyomott lézerimpulzusok eltérő fizikai hatása jól demonstrálható a rhodamine 6G festékből készített oldat segítségével. Míg az időben megnyújtott impulzusok esetében semmilyen fényjelenséget sem észlelünk az oldatban, addig az impulzuskompresszor után a fényútba helyezve a festékoldattal teli lombikot, látványosan vílágít az oldat azon a részen, ahol az összenyomott impulzusok áthaladtak rajta.
Az impulzusnyújtó feladata a csúcsintenzitás csökkentése anélkül, hogy az impulzus összenergiája a jelentősen csökkenne. Erre "természetes" módon is lehetőség van, hiszen kellő hatást érhetünk el akkor is, ha nagy diszperzióval rendelkező anyagon, pl. üvegtömbön, üvegszálon vezetjük át a nyalábot. Bizonyos bemeneti és kimeneti impulzus-paraméterek esetén ez a megoldás nem alkalmazható hatékonyan, vagy túl nagy helyet foglalna el. Megfelelő nagyságú nyújtást érhetünk el úgy, hogy spektrális bontóelem segítségével szögdiszperziót hozunk létre a nyalábban, majd a térben elkülönített komponenseket úgy irányítjuk, hogy azok különböző optikai úthosszakat fussanak be. Az elsővel megegyező paraméterekkel rendelkező bontóelem alkalmazásával a komponensek újra párhuzamossá tehetők. Ekkor azonban még jelentős térbeli csörp és impulzusfrontdőlés van a nyalábban, így újabb két, az eredetiekkel tükörszimmetrikusan álló bontóelemre van szükségünk (lásd 7.2. ábra), amellyel ezek a nem kívánatos torzulások kompenzálhatóak. Ugyanezt a hatást érhetjük el, ha egy visszafordító végtükör segítségével a nyalábot az eredetivel megegyező, de ellentétes irányú úton újra átküldjük a két első bontóelemen.

7.2. ábra. Négy prízmából álló impulzusnyújtó sematikus rajza.
A két legegyszerűbb bontóelemnek, a prizmának és az optikai rácsnak megfelelően az impulzusnyújtóknak kétféle megvalósítási formája van (lásd animációk: prizmás stretcher, rácsos stretcher). A prizmás impulzusnyújtó előnye, hogy a rácsos megoldáshoz képest kisebb a reflexiós veszteség, míg a rácsos impulzusnyújtó alkalmazásával jó közelítéssel lineáris a kimeneti impulzus diszperziója, valamint egyszerűbb nagy nyújtást elérni.
Az impulzusok időbeli nyújtása ezek alapján nem tűnhet komplikált feladatnak, azonban számos aberráció léphet fel, melyeket lehetőség szerint kompenzálnunk kell. Arról már esett szó, hogy a kétpasszos prizma- illetve rácspár kialakítású nyújtó hogyan kompenzálja a térbeli csörpöt. A bontóelemek egymással szembe néző felületeinek a lehető legjobban párhuzamosnak kell lennie, a legkisebb horizontálisan vagy vertikálisan bezárt szög esetén is a nyaláb valamekkora visszamaradó szögdiszperzióval fog rendelkezni, ami gyengíti az erősítést és az azt követő kompresszálás hatásfokát. A szférikus aberráció legegyszerűbben úgy kerülhető el, ha egy gömbtükröt alkalmazunk, melynek fókuszában helyezkedik el az első rács (lásd 7.3. ábra).

7.3. ábra. Tipikus rácsos impulzusnyújtó vázlatos felépítése.
Mind a prizmás, mind a rácsos impulzusnyújtók esetén problémát okoznak a magas rendű diszperziós komponensek, mivel ezek precíz kompenzálása csupán a kompresszor segítségével szinte lehetetlen. Ha azonban a kétféle bontóelemet egyesítjük, azaz egy prizma egyik oldalán egy megfelelő osztású rácsot hozunk létre (az ilyen optikai elemeket a szakirodalomban grism-nek nevezik), igen hatékonyan csökkenthetjük a magasrendű diszperziós együtthatók hatását.
Az impulzuskompresszorok feladata a nyújtókéval éppen ellentétes, így működésük és a fellépő nehézségek is közel azonosak (lásd animációk: prizmás kompresszor, rácsos kompresszor). A legnagyobb különbség az impulzusok megnövekedett intenzitásában mutatkozik, ami miatt a kompresszorok optikai elemeinek nagy impulzusintenzitás-tűréssel kell, hogy rendelkezzenek, illetve, mivel ez a nyaláb átmérőjének növelésével mérsékelhető, nagy felületre is szükség van. Prizmákat impulzuskompesszorként általában csak a lézeroszcillátorok rezonátorában alkalmaznak, mert a prizma anyagában erős nemlineáris jelenségek lépnének fel nagy intenzitások esetén, amik nehezítik a transzformlimitált impulzusidő elérését. A rácsos impulzuskompresszorok ötlete E.B.Treacy [7.4], megvalósítása és hullámoptikai leírása pedig O.E.Martinez [7.5, 7.6] nevéhez fűződik.
A kompresszor esetében fellépő problémák némiképp csökkenthetők olyan módon, ha az impulzusnyújtóban negatív diszperziót hozunk létre, így az erősítőbeli terjedést is figyelembe véve, az impulzusnyújtó megfelelő tervezése esetén akár egy normális diszperzióval rendelkező üvegtömb is alkalmas lehet az impulzusok kompresszálására.
A CPA rendszerek impulzusnyújtó és -összenyomó egységeinek rácsaival vagy prizmáival igen körülményes a spektrális fázis pontos visszaállítása és szabályozása, pontosabban a magasabb rendű fázisderiváltak egymástól független vezérlése, ezért egyre nőtt az igény olyan eszközök kifejlesztésére, melyekkel a spektrális fázis finomhangolása könnyen megoldható. Számos megoldási javaslat született, például az impulzusnyújtó illetve -összenyomó rendszerek Fourier-síkjában elhelyezett folyadékkristályos szabályzók [7.7], fénnyel indukált impulzusformáló eszközök [7.8], hőmérsékletvezérelt üvegtömb [7.9], vagy deformálható tükrök [7.10]. Ezek a módszerek többnyire a 7.4. ábrán feltüntetett optikai elrendezésen alapulnak, ahol a fázismoduláló eszköz a lencsepár Fourier-síkjában helyezkedik el.

7.4. ábra. Fourier-transzformációs impulzusformálás sémája. A térben elkülönített spektrális komponensek fázisa a Fourier-síkban elhelyezett eszköz segítségével szabályozható
Az impulzusok precíz formálására használható eszközök közül azonban a programozható akusztooptikai diszperziós szűrők (acousto-optical programmable dispersive filter -AOPDF, [7.11]) alkalmazása terjedt el legszélesebb körben, így ezt vizsgáljuk meg egy kicsit részletesebben. Az AOPDF kiválóan alkalmas CPA-rendszerek kompresszió előtti szakaszaiban az impulzusok spektrális fázisának és ezen keresztül időbeli alakjának pontos beállítására éppúgy, mint az impulzus amplitúdójának vezérlésére. Felhasználásának talán az egyetlen korlátozását csak az jelenti, hogy sérülékeny, így erősített impulzusok vezérlésére, közvetlenül a céltárgy előtt nem használható. Az impulzusnyújtó és az erősítő között elhelyezve azonban minden további nélkül alkalmazható.

7.5. ábra. Egy programozható akusztooptikai diszperziós szűrő (AOPDF) működési elve
Az infravörös tartományra tervezett eszköz működése egy kettőstörő TeO2 kristályban, a belépő fénnyel kollineárisan terjedő akusztikus hullám diffrakciós hatásán alapszik, melyet rádiófrekvenciás jel segítségével hozunk létre (lásd 7.5. ábra). A belépő fény és az akusztikus hullám kölcsönhatását a
 |
(7.1) |
egyenlet írja le, ahol k be , k ao és k diff a belépő nyaláb, az akusztikus hullám, illetve a diffraktált nyaláb hullámszámvektora. A fázisillesztés feltételének teljesülése esetén a különböző hullámok közötti csatolódás következtében a diffraktált nyaláb polarizációja a belépő fény rezgési síkjára merőleges lesz. A diffraktált fény elektromos térerősségének nagysága az
 |
(7.2) |
összefüggés szerint az E belépő (t) belépő elektromos térerősség és az S(t/σ) rádiófrekvenciás jel konvolúciós szorzatával arányos. A
 |
(7.3) |
egy skálázási faktor, amely az n eo extraordinárius és n o ordinárius törésmutató különbségének és az akusztikus hullám v, illetve a fény c vákuumbeli terjedési sebességeiből számolt hányados szorzataként számolható ki, értéke a σ≈10-7 nagyságrendbe esik. A frekvenciatérben a (7.2) egyenlet az
 |
(7.4) |
formában írható fel. Ha a belépő fény szélessávú impulzus, akkor rádiófrekvenciás jelgenerátort alkalmazva σ szerint megfelelően skálázott elektromos impulzust kell előállítanunk. A kristályban terjedő, a fénysebességhez képest gyakorlatilag mozdulatlan akusztikus hullám felveszi a rádiófrekvenciás jel időbeli alakját. A rádiófrekvenciás jel vezérlésével az akusztikus hullám csörpölhető. Ezzel azt érjük el, hogy a fény különböző frekvenciájú komponensei az általunk meghatározott helyen fognak diffraktálódni. Mivel a kölcsönhatás után a fény már extraordinárius sugárként az ordináriustól eltérő terjedési sebességgel halad tovább, a diffrakció helyének változtatásával a diffraktált impulzusok spektrális fázisa a kívánt alakúra formálható.
A diszperzió kompenzálása mellett CEP-stabilizálásra és néhány ciklusú impulzusok karakterizálására is kiválóan alkalmazható. Felhasználási köre nem korlátozódik az infravörös tartományra, léteznek a látható és ultraibolya spektrális tartományon működő AOPDF-ek is.
Milyen alternatív megoldások lehetségesek impulzusnyújtás végrehajtására?
Milyen előnyei és hátrányai vannak az optikai parametrikus erősítésnek a titán-zafírral történő erősítéshez képest?
Megvalósítható lenne-e egy olyan impulzusnyújtó/kompresszor, amely egy prizmából és egy rácsból áll?
Megvalósítható lenne-e egy olyan impulzusnyújtó/kompresszor, amely különböző rácsállandóval rendelkező rácsokból áll?
Megvalósítható lenne-e egy olyan impulzusnyújtó/kompresszor, amely különböző anyagú és törőszögű prizmákból áll?
Mi az AOPDF eszközök használatának legfőbb előnyei a Fourier-transzformációs impulzusformáláson alapuló módszerekkel szemben?
[7.1] H. R. Telle, G. Steinmeyer, A. E. Dunlop, J. Stenger, D. H. Sutter, U. Keller, "Carrier-envelope offset phase control: A novel concept for absolute optical frequency measurement and ultrashort pulse generation," Appl. Phys. B 69 , 327–332 (1999).
[7.2] D. Strickland, G. Mourou, "Compression of amplified chirped optical pulses," Optics Communications 55, 447-449 (1985).
[7.3] A. Dubeitis, G. Jonasauskas, A. Piskarskas, "Powerful femtosecond pulse generation by chirped and stretched pulse parametric amplification in BBO crystal," Optics Communications 88, 437-440 (1992).
[7.4] E. Treacy, "Optical pulse compression with diffraction gratings," IEEE Journal of Quantum Electronics 5, 454-458 (1969).
[7.5] O. E. Martinez, "Grating and prism compressors in the case of finite beam size," Journal of Optical Society of America B 3, 929-934 (1986).
[7.6] O. E. Martinez, "Design of high-power ultrashort pulse amplifiers by expansion and recompression," IEEE Journal of Quantum Electronics 23, 1385-1387 (1987).
[7.7] J. C. Vaughan, T. Feurer, K. W. Stone, K. A. Nelson, "Analysis of replica pulses in femtosecond pulse shaping with pixelated devices," Optics Express 14, 1314-1328 (2006).
[7.8] C. Dorrer, F. Salin, F. Verluise, J. P. Huignard, "Programmable phase control of femtosecond pulses by use of nonpixelated spatial light modulator," Optics Letters 23, 709-711 (1998).
[7.9] K. Osvay, K. Varjú, G. Kurdi, "High order dispersion control for femtosecond CPA lasers," Applied Physics B 89, 565-572 (2007).
[7.10] F. Duron, G. Cheriaux, J. Faure, J. Nees, M. Nantel, A. Maksimchuk, G. Mourou, J. C. Chanteloup, G. Vdovin, "Wave-front correction of femtosecond terawatt lasers by deformable mirrors," Optics Letters 23, 1043-1045 (1998).
[7.11] P. Tournois, "Acousto-optics programmable dispersive filter for adaptive compensation of group delay time dispersion in laser systems," Optics Communications 140, 245-249 (1997).
Tartalom
A fényimpulzusokat használó kísérleteknél sokszor cél a nagy energiasűrűség, vagy teljesítmény elérése [8.1, 8.2], amit például lencsével illetve tükörrel történő fókuszálással lehet elérni. A nagyobb teljesítmények elérésének egyik lehetséges módja az impulzus időbeli hosszának csökkentése. Transzformlimitált impulzusok esetén az impulzushossz csökkenésével a spektrális szélesség növekszik, aminek következtében a femtoszekundumos tartományban a fókuszált fényimpulzusok viselkedése jelentősen eltér a jól ismert monokromatikus esettől. A fókuszáló elem hatását először egy egyszerű - a geometriai optikán alapuló - modellel, majd egy hullámoptikai leírást használva vizsgáljuk meg. A hullámoptikai leírásnál az impulzusok terjedésének leírásánál szokásosan használt Fourier-féle módszert fogjuk alkalmazni, vagyis a beeső impulzust monokromatikus hullámok szuperpozíciójaként fogjuk fel. A fókuszáló optikai elemnek a monokromatikus komponensekre gyakorolt hatását figyelembe véve, majd a monokromatikus komponenseket összeadva megkapjuk az impulzus térerősségét. Fókuszálás során a beeső hullám frontját a fókuszáló optikai elem úgy változtatja meg, hogy a kilépő hullám egy adott pont (a képpont, amely többnyire a fókuszpont) felé tartó gömbhullám lesz [8.3, 8.4]. A fókuszáló elem hullámfrontra gyakorolt hatását vízhullámokkal végzett kísérlettel könnyen szemléltethetjük. A 8.1. ábrán egy vízhullámokat fókuszáló lencse (balra) és egy homorú tükör (jobbra) látható.

8.1. ábra. Gyűjtő lencse (balra) és homorú tükör (jobbra) fókuszáló hatásának szemléltetése vízhullámokkal.
A felvételeken és a kísérletekről készült filmeken egyaránt jól kivehetjük a fókuszált hullám kör alakú hullámfrontjait, amely nyilván felületi hullámokra a háromdimenziós gömb alakú frontok kétdimenziós megfelelői. Teljesen hasonló dolog történik a fény esetében is, csak ott a hullámfrontokat közvetlenül nem látjuk. A lencse és a tükör a számolás szempontjából lényegesen nem különbözik. Mindkét eset visszavezethető egy kör alakú nyíláson áthaladó konvergens gömbhullám elhajlására. A következőkben a lencse esetét vizsgáljuk meg, azonban a megállapítások többsége tükör esetén is érvényes. nyilván figyelembe kell venni, hogy a kromatikus aberráció tükör esetén nem lép fel, amely egyik lehetséges előnye lehet a tükrök alkalmazásának.
Leképezési hibák (aberrációk) jelenlétében a kilépő hullámfront az aberráció mértékétől függően eltér ettől az ideális gömb(süveg) alaktól. Az eltérés mértékét az ún. aberráció-függvény méri [8.5]. Ezen fejezetben az aberrációk közül csak a kromatikus aberráció hatásával fogunk foglalkozni. A monokromatikus aberrációk hatását a 9. fejezetben tárgyaljuk majd.
Tegyük fel, hogy egy λ0 központi hullámhosszúságú rövid impulzus merőlegesen esik be egy D0 vastagságú lencsére (8.2. ábra), jelölje a0 a lencse nyílásának sugarát és f0 a lencse λ0 hullámhosszon mért fókusztávolságát. A lencsén való áthaladás során két fontos jelenség lép fel. Egyrészt az impulzusfront késik a fázisfronthoz képest: Ugyanis, az impulzusfront vg = c/ng csoport-, míg a fázisfront a vp = c/n0 fázissebességgel terjed, ahol n0 = n(λ0) és ng = n0 - λ0 n'(λ0) a λ0 hullámhosszhoz tartozó törésmutató illetve csoportindex. A szokásos normális diszperzió esetén (n'(λ0) < 0 miatt) a csoportsebesség általában a fázissebességnél kisebb. Ezért az impulzusfront lemarad a fázisfronthoz képest. Másrészt a diszperzív közegbeli terjedés miatt a terjedési hosszal arányosan kiszélesedik.

8.2. ábra. A lencsén belül a csoportsebesség kisebb, mint a fázissebesség, ezért egy adott sugár mentén a csoportsebességgel terjedő impulzusfront lemarad a gömb alakú fázisfronthoz képest.
Az impulzusfront az optikai tengelytől a távolságra belépő sugár mentén a 8.2. ábrán látható - az A belépési síktól egy adott (aberrációmentes esetben gömb alakú) fázisfrontig terjedő L1 + L2 + L3 + L4 utat
 |
(8.1) |
idő alatt teszi meg, ahol a lencsét körülvevő közeg törésmutatóját 1-nek feltételeztük. Hasonlóan a fázisfront terjedési ideje
 |
. | (8.2) |
Ebből az impulzusfront késése a fázisfronthoz viszonyítva
 |
. | (8.3) |
Paraxiális közelítést használva
 |
, | (8.4) |
ahol R1 és R2 a lencse felületeinek a görbületi sugara. Ez alapján az paraxiális közelítésben
 |
. | (8.5) |
A görbületi sugarakat kiküszöbölhetjük a jól ismert
 |
, | (8.6) |
"lencsekészítők egyenletének" a segítségével, és így végeredményként a
 |
(8.7) |
összefüggéshez jutunk a késésre. Az utolsó alak származtatásánál ismét kihasználtuk "lencsekészítők egyenletét". Ez utóbbi összefüggés azért is fontos, mert univerzális alakú, ami azt jelenti, hogy más fókuszáló elemet vizsgálva ugyanezen összefüggést kapjuk meg [8.6]. Ez alapján látható, hogy kromatikus aberráció jelenlétekor, mikor f '(λ0) nem zérus, egy adott sugár mentén a belépő sugárnak az optikai tengelytől mért a távolságának négyzetével arányosan késik az impulzusfront a fázisfronthoz képest. A késés az optikai tengelyen (a = 0) a legnagyobb, és a szélső sugárra (a = a0) vonatkozólag zérus. Akromatikus esetben (f '(λ0) = 0) nincs késés a két front között, vagyis erre az esetre a geometriai optikai modell gömb alakú impulzusfrontot jósol.
Mivel a vizsgált probléma hengerszimmetriával rendelkezik, az impulzusfront alakját - és később az elektromos térerősség helyfüggését is - célszerű hengerkoordinátákkal leírni. Helyezzük a vonatkoztatási rendszer origóját az F0 fókuszpontba és legyen a z-tengely az optikai tengely. Továbbá az idő nullpontját válasszuk úgy meg, hogy az optikai tengely mentén az impulzusfront a t = 0 időpontban érjen a fókuszba. Aberrációk hiányában a gömb alakú fázisfront a lencse mögött az a paraméterrel adott (0 ≤ a ≤ a0) sugár mentén c sebességgel terjed, így a t időpontban a helyét a
 |
(8.8) |
koordináták írják le, ahol α = arctg(a/f0). A (8.8) egyenlet a (z, r) síkban egy körcikknek a paraméteres egyenlete. Ezt a z-tengely körül megforgatva kapjuk a gömbsüveg alakú fázisfrontot. A (8.8) egyenletbeli ΔT(0) időeltolás azt fejezi ki, hogy a fázisfront a t = -ΔT(0) időpontban - egyetlen ponttá összezsugorodva - halad át a fókuszponton, összhangban azzal, hogy ΔT(0) idővel siet az impulzusfronthoz képest. Mivel az impulzusfront az a paraméterrel adott sugár mentén ΔT(a) idővel késik a fázisfronthoz képest, így a helyzetét a t időpontban a
 |
(8.9) |
egyenletekkel definiált paraméteres görbe írja le, ahol 0 ≤ a ≤ a0. A (8.9) egyenletből meghatározhatjuk azt az - a paramétertől függő - tF időpontot, amikor az impulzusfront az a paraméter adott sugár mentén éppen áthalad a (0, 0) koordinátákkal adott fókuszponton. A tF időpontra a tF + ΔT(0) - ΔT(a) = 0 egyenlet teljesül, amiből
 |
. | (8.10) |
Az 0 ≤ a ≤ a0 relációból következik a -T0 ≤ tF ≤ 0 egyenlőtlenség, ahol
 |
. | (8.11) |
A -T0 ≤ tF ≤ 0 reláció azt mutatja, hogy az impulzus a -T0-tól 0-ig tartó időintervallumban halad át a fókuszponton. Mégpedig úgy, hogy kezdetben (t = -T0 -kor) a szélső sugár mentén, majd egyre inkább belső sugarak mentén, legvégül (t = 0 -kor) a tengely menti sugáron megy keresztül a fókuszon. Ez alapján a (8.11) egyenlet éppen azt időtartamot adja meg, amely alatt az impulzus áthalad a fókuszponton.
A (8.9) egyenletből kiszámítottuk az impulzusfrontot különböző időpontokra, λ0 = 249 nm központi hullámhosszúságú impulzust és egy a0 = 40 mm sugarú, f0 = 150 mm fókusztávolságú kvarc lencsét (n0 = 1.50799, λ0 n'(λ0) = -0.1375 és f '(λ0) = 163.0898 mm/μm) feltételezve. A számolás eredményt a 8.3. ábra szemlélteti. Látható, hogy a kromatikus aberráció következtében, fókuszpont előtti tartományban egy lópatkóhoz hasonló alakú impulzusfront alakul ki, amely a fókuszponthoz érve "befűződik", és így egy hurok alakú impulzusfront keletkezik. A fókuszpontban először a lencse széléről, majd egyre beljebb lévő sugarak mentén érkezik fény, végül a t = 0 időpontban a tengely menti sugáron halad át az impulzus a fókuszon. Ennek következtében a fókuszpontban az impulzus időben jelentősen kiszélesedhet. A számolásnál használt lencse esetén T0 = 4816 fs idő alatt halad át az impulzus a fókuszon. Ennek következtében például egy eredetileg 100 fs-os fényimpulzus, - melyre a szokásos lencsevastagságokra a diszperzió okozta kiszélesedés még nem jelentős - gyakorlatilag 4816 fs hosszúságúra szélesedik fókuszban. Ez a kiszélesedés természetesen jelentősen lecsökkenti az elérhető fókuszbeli intenzitást. Az impulzusfront terjedését a mellékelt animáció szemlélteti.

8.3. ábra. Egy f0 = 150 mm fókusztávolságú, a0 = 40 mm sugarú kvarc lencsén áthaladó λ0 = 249 nm központi hullámhosszúságú impulzus impulzusfrontjai a -11 ps, -7 ps, -3 ps, 1 ps és az 5 ps időpontokban. A -3 ps-nál is látható hurok alakú impulzusfront miatt az impulzus T0 = 4816 fs alatt halad keresztül a fókuszon.
A geometriai optikai modellel kapcsolatban azonban nem szabad elfeledkezni arról, hogy a geometriai optika érvényessége éppen az alkalmazások szempontjából fontos tartományban, a fókuszpont környezetében és az árnyékhatár közelében érvényét veszti, továbbá nem tartalmazza az elhajlás és az interferencia miatt fellépő jelenségeket sem. Így a modell eredményét csak közelítésnek érdemes tekinteni és mindenképpen érdemes összevetni a diffrakcióról és az interferenciáról is számot adó hullámoptikai számolásból adódó eredménnyel.
Tegyük fel, hogy a lencsére egy sík impulzusfronttal rendelkező, ω0 központi körfrekvenciájú, b(t) burkolóval leírható fényimpulzus esik merőlegesen. Közvetlenül a lencse előtti - a 8.4. ábrán az A - síkban a térerősség időfüggését
 |
, | (8.12) |
egyenlet írja le, ahol tA az A síkban mért (helyi) idő, s(t) a térerősség időbeli burkolója és A0 a maximális amplitúdó. Az lokális idő nullpontját úgy választjuk meg, hogy a burkoló maximumát a tA = 0 pillanatban vegye fel, vagyis a beeső impulzusfront a tA = 0-kor legyen az A síkban. Monokromatikus aberrációk hiányában a lencse az impulzust alkotó monokromatikus komponenseket a frekvenciájukhoz tartozó fókuszpont irányába tartó konvergens gömbhullámokká alakítja át, melyek hullámfrontját a lencse nyílása kivágja. Ez alapján a probléma visszavezethető egy kör alakú nyíláson áthaladó és elhajló gömbhullám vizsgálatára. A lencse fázistolása miatt a fényimpulzust alkotó ω körfrekvenciájú komponensnek közvetlenül a lencse mögötti f = f(ω) sugarú W gömbsüveg alakú hullámfelületén (lásd a 8.4. ábrát) a térerősség
 |
, | (8.13) |
ahol S(ω) az s(t) burkoló Fourier-transzformáltja, n(ω) a lencse anyagának törésmutatója és D0 a lencse vastagsága.

8.4. ábra. A fókuszálás leírásánál használt koordinátarendszer és a jelölések értelmezése. Az origót az ω0 központi körfrekvenciájú fókuszpontba helyezzük és a lencse optikai tengelye a z-tengely. A térerősség hengerszimmetrikus, ezért csak z és az r hengerkoordinátáktól függ.
A fókuszpont környezetében a monokromatikus komponensek térerőssége a diffrakciós integrállal számítható ki [8.3, 8.4]:
 |
, | (8.14) |
ahol λ = 2πc/ω a vákuumbeli hullámhossz, k = (ω/c) körhullámszám és az integrálást a W hullámfelületre kell elvégezni. A zárójelben lévő kifejezés - [8.4] alapján - az
 |
(8.15) |
alakba írható, ahol
 |
, | (8.16) |
és J0 a nulladrendű Bessel-féle függvényt jelöli, továbbá
 |
. | (8.17) |
A lencse mögötti térerősséget a monokromatikus komponensek szuperpozíciója szolgáltatja, azaz
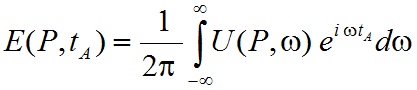 |
. | (8.18) |
Érdemes megjegyezni, hogy az Y(u, v) függvény kifejezhető az U1(u, v) és az U2(u, v), illetve a V0(u, v) és a V1(u, v) Lommel-féle függvényekkel [8.4], melyek numerikusan könnyen számolhatók, mert az őket definiáló függvénysorok konvergenciája gyors. Továbbá az itt leírt - homogén megvilágításra vonatkozó - formalizmus változtatás nélkül alkalmazható Gauss-eloszlású megvilágítás esetére is az u paraméter és a Lommel-féle függvények komplex síkra való kiterjesztésével [8.7].
A (8.13) egyenletben lévő (ω/c) n(ω) kifejezést
 |
(8.19) |
alakba írva, azaz a (ω/c) n(ω) mennyiség ω0 körüli lineáris közelítésének és az ω0 és ω-tól függő M maradéktagjának összegeként előállítva, valamint tA-ról a
 |
(8.20) |
összefüggéssel definiált időváltozóra áttérve, a térerősséget - fentiekben elmondottakat felhasználva - az
 |
(8.21) |
formulával számíthatjuk ki, ahol vg a lencse anyagában a csoportsebesség és Φ0 egy frekvenciától független fázisállandó:
 |
. | (8.22) |
Látható, hogy a (8.20) egyenletbeli idő azzal az idővel különbözik a tA időtől, amennyi idő alatt az impulzusfront az optikai tengelyen az A síktól az F0 fókuszpontig eljut. Ez azt jelenti, hogy a hullámoptikai leírásban használt t idő azonos a geometriai optikai leírásnál idővel, így a számolási eredmények könnyen összehasonlíthatók.
A (8.21) egyenletből kiszámított I = | E |2 intenzitást a t = -11 ps és a t = 1 ps időpontokra a 8.5. ábra szemlélteti, ahol a számolásnál az M = 0 feltételezéssel éltünk, azaz a lencse fázistolásának második deriváltjával arányos kiszélesedést és a magasabb rendű deriváltak okozta egyéb torzító hatásokat elhanyagoltuk. A számolás eredménye az mutatja, hogy a geometriai optikai modell jól írja le az impulzusfront terjedését (szaggatott vonal a betétábrákon). Az ábrán szintén látható a hullámoptikai leírásnak talán az egyik leginkább meglepő eredménye: az optikai tengelyen (r = 0) egy a beeső impulzussal azonos időbeli lefutású - az ábrán kis tüskeként megjelenő - impulzus terjed [8.8, 8.9], meglepő módon a vákuumbeli fénysebességnél nagyobb - azaz ún. szuperluminális - sebességgel. Az impulzus helyének, sebességének és a radiális függésének vizsgálata arra utal, hogy a lencse nyílásának a peremével hozható kapcsolatba [8.8, 8.9]. A diffrakciós integrálból kiindulva megmutatható [8.10], hogy ezen impulzus a lencse nyílásának széléről (pereméről) kiinduló elemi hullámok szuperpozíciója hozza létre, ezért ezt az impulzust szélihullám-impulzusnak nevezték el, az angol nyelvű szakirodalomban a boundary wave pulse nevet kapta. A szélihulám-impulzus a 8.5. ábrán egy kis tüskeként jelenik meg. A számolás térbeli lépésköze nem elég finom a radiális intenzitás-eloszlás megjelenítéséhez. Megmutatható, hogy a 8.9. ábrán látható radiális függés a J0 Bessel-függvénnyel írható le [8.8, 8.10]. A geometriai optika által is leírt főimpulzus és a szélihullámimpulzus terjedését a mellékelt animáció [8.11] szemlélteti.

8.5. ábra. Kromatikus aberrációval rendelkező kvarc lencsén áthaladó 100 fs hosszúságú, Gauss-os időbeli burkolójú, 249 nm központi hullámhosszú fényimpulzus térbeli intenzitás-eloszlása a fókuszpont előtt (balra) és mögött (jobbra) homogén megvilágítás esetén. A betétábrákon az intenzitás egy szintvonalát folytonos, a geometriai optikai modellből adódó impulzusfrontot szaggatott vonal szemlélteti.
A fókuszsíkbeli intenzitás időfüggését a 8.6. ábra szemlélteti. Ez azt mutatja, hogy a geometriai optikai modellből kapott 4816 fs időbeli hossz a példaként vett esetben igen jó becslésnek tekinthető. Homogén térbeli megvilágítás esetén (az ábrán balra) gyors felfutás, és ugyanilyen lefutás között az intenzitás állandó [8.8, 8.9]. Elhanyagolható csonkoltságú Gauss-eloszlású megvilágításra - vagyis csonkolatlan Gauss-nyalábra - az intenzitás exponenciálisan emelkedve éri el a maximumát, majd gyorsan lecsökken [8.12]. Az ábráról az is megfigyelhető, hogy a fókuszsíkban az intenzitás-eloszlás egy időben növekvő sugarú, világos-sötét mintázatú, középen világos foltot tartalmazó, koncentrikus interferencia-gyűrűrendszer.

8.6. ábra. Kromatikus aberrációval rendelkező kvarc lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus intenzitásának az időfüggése a fókuszsíkban (z = 0) a lencsének térben homogén (balra) illetve Gauss-eloszlású (jobbra) megvilágítása esetén.
A 8.7. ábra a fókuszpontbeli térerősség burkolójának az időbeli lefutást szemlélteti. Az intenzitás ennek négyzetével arányos. A számolásnál a0 = 20 mm paramétert használtuk, amely fele az előző számolásnál használt értéknek. A (8.11) egyenlet alapján azt várjuk, hogy a0 értékét felére csökkentve, az időbeli kiszélesedés a negyedére csökken. Az ábrán látható, hogy ez így is történik, továbbá a (8.11) egyenlettel definiált T0 mennyiség a burkoló félértékszélességét adja meg.

8.7. ábra. Kromatikus aberrációval rendelkező kvarc lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus burkolójának az időfüggése a fókuszpontban (z = 0, r = 0) a lencsének térben homogén, illetve Gauss-eloszlású megvilágítása esetén. Az a-részen a (8.21) egyenletből számolt burkolót a vonal, míg a közelítéssel kapott (8.23) formulával számolt burkolót a kis tömör körök szemléltetik. A b-részen a beeső nyaláb csonkolásának hatása látható.
Itt nem részletezett módon megmutatható [8.9], hogy homogén megvilágítás esetén a fókuszpontbeli térerősség az
 |
(8.23) |
formulával számolható ki, ahol Fs(t) az s(t) burkoló integrálfüggvénye:
 |
. | (8.24) |
Hasonló formula érvényes Gauss-eloszlású megvilágítás esetén, csak az integrálfüggvény előtt, és az integranduszban is megjelenik egy exponenciális szorzótényező [8.9]. A beeső nyaláb csonkolásának hatása a [8.7] hivatkozásban leírt módon tárgyalható. A 8.7. ábra b-része a lencse nyílásának csonkoló hatását szemlélteti. A beeső Gauss-nyaláb csonkolását a κ = (a0/w0)2csonkolási együttható jellemzi, ahol w0 a beeső nyaláb nyalábnyaka. A κ = 0 felel meg a homogén megvilágításnak, míg 4 ≤ κ esetén a nyaláb csonkolása elhanyagolható [8.7].
Aberrációk hiányában a (8.21) egyenletből számolt intenzitás-eloszlást szemlélteti a 8.8. ábra.

8.8. ábra. Akromatikus lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus térbeli intenzitás-eloszlása a fókuszpont előtt (balra) és mögött (jobbra) homogén megvilágítás esetén. A betétábrákon az intenzitás egy szintvonalát folytonos, a geometriai optikai modellből adódó impulzusfrontot szaggatott vonallal rajzoltuk fel.
A geometriai optikai modellből számolt impulzusfrontot szaggatott vonal jelöli. Látható, hogy a szélihullám-impulzus akromát lencse esetén is megjelenik. Az impulzus terjedését a mellékelt animáció [8.11] szemlélteti, melyen jól megfigyelhetjük a főimpulzus és a szélihullámimpulzus interferenciája miatt megjelenő mintázatot. Aberrációmentes esetben a fókuszpont előtt a gömbsüveg alakú impulzusfront megelőzi, a fókuszpont után lemarad a szélihullám-impulzushoz képest, ahogy az a 8.8. ábrán is látszik, és a mellékelt animáción is látható. A diffrakciónak van egy - eredetileg még Thomas Youngtól származó - értelmezése [8.10], amely szerint az elhajlás során a nyílás mögötti hullám előáll a nyíláson zavartalanul tovaterjedő és a nyílás pereme által generált szélihullám szuperpozíciójaként. Megmutatható, hogy az elhajlási problémák leírásánál konvencionálisan alkalmazott Fresnel-féle értelmezés matematikai megfogalmazásának tekinthető diffrakciós integrál valóban szétbontható két ilyen hullám összegére [8.10]. Az animáción a nyíláson áthaladó és zavartalanul tovaterjedő konvergens gömbhullámot piros, míg a nyílás pereméről kiinduló hullámot kék szín szemlélteti. A lencse pereme által generált szélihullámok vízhullámokkal végzett kísérletben jól megfigyelhetők. Rövid impulzusok esetén a zavartalanul terjedő hullám és a szélihullám, pontosan a rövid impulzushossz miatt, gyakran térben elkülönülten jelenik meg. Az elhajlásnak a Young-féle értelmezése ezért rövid impulzusok esetén sokszor szemléletesebb, vagyis könnyebben értelmezhetőbb, mint a Fresnel-féle értelmezést használva. A szélihullám-impulzus radiális eloszlását a 8.9. ábra mutatja. Érdemes megemlíteni, hogy a szélihullám-impulzus létét kísérletileg többféle módszerrel is igazolták [8.13, 8.14]. A számolások és a mérések között jó egyezés van.

8.9. ábra. A szélihullám-impulzus radiális eloszlása [8.13].
Hogyan számítható ki a lencse anyagában a fázis- és a csoportsebesség?
Hogyan befolyásolja a kromatikus aberráció egy fókuszált rövid fényimpulzus impulzusfrontját?
Milyen hatása van a kromatikus aberrációnak a fókuszpontban az impulzus időbeli lefutására?
Fogalmazza meg az elhajlás Fresnel- és Young-féle értelmezéseit!
Mit nevezünk szélihullám-impulzusnak, és hogyan értelmezhető a létrejötte?
Mit jelent a szuperluminális szó?
[8.1] J. C. Diels and W. Rudolph, Ultrashort Laser Pulse Phenomena, (Academic Press, 2nd edition).
[8.2] A. M. Weiner, Ultrafast Optics, (Wiley)
[8.3] J. W. Goodman, Introduction to Fourier Optics (McGraw-Hill Book Company, 1968), chapter. 2-3.
[8.4] M. Born and E. Wolf, Principles of Optics, chapter 8.8 (Cambridge University Press, 7th edition).
[8.5] M. Born and E. Wolf, Principles of Optics, chapter 9 (Cambridge University Press, 7th edition).
[8.6] Zs. Bor, Distortion of femtosecond laser pulses in lenses and lens systems, J. Mod. Opt. 35 (1988), 1907.
[8.7] Z. L. Horváth and Zs. Bor, Focusing of truncated Gaussian beams, Optics Commun. 222 (2003) 51.
[8.8] Zs. Bor, Z. L. Horváth, Distortion of Femtosecond Pulse in Lenses. Wave Optical Description, Optics Commun. 94 (1992) 249-258.
[8.9] Z. L. Horváth and Zs. Bor, Behaviour of Femtosecond Pulses on The Optical Axis of a Lens. Analytical Description, Optics Commun. 108 (1994) 333-342.
[8.10] Z. L. Horváth and Zs. Bor, Diffraction short pulses with boundary wave theory, Phys. Rev. E 63 (2001) 26601.
[8.11] U. Fuchs, U. D. Zeitner and A. Tünnermann, Ultra-short pulse propagation in complex optical systems, Optics Express 13 (2005) 3852.
[8.12] Z. L. Horváth, Zs. Bor, Focussing of Femtosecond Pulses Having Gaussian Spatial Distribution, Optics Commun. 100 (1993) 6-12.
[8.13] Z. L. Horváth, J. Klebniczki, G. Kurdi and A. P. Kovács, Experimental investigation of boundary wave pulse, Optics Commun. 239 (2004) 243.
[8.14] P. Saari, P. Bowlan, H. Valtna-Lukner, M. Löhmus, P. Piksarv and R. Trebino, Basic diffraction phenomena in time domain, Opt. Express 18 (2010) 11083-8.
Tartalom
Az előző fejezetben megvizsgáltuk, hogy a fókuszáló optikai elem kromatikus aberrációja milyen hatással van egy ultrarövid fényimpulzus terjedésére. Akkor a monokromatikus aberrációk hatását elhanyagoltuk. Most azt vizsgáljuk meg, hogy az egyes monokromatikus aberrációk hatása hogyan tárgyalható. Az aberrációkkal kapcsolatos alapfogalmakat és természetüket ismertnek tekintjük, itt első sorban azokra a részletekre térünk csak ki, amelyek a rövid fényimpulzusok terjedésének leírásánál mindenképpen szükségesek.
A hullámfrontnak az ideális gömb alaktól való eltérését a Φ aberrációfüggvénnyel szokás megadni [9.1]. Az aberrációfüggvény értelmezését a 9.1. ábrán láthatjuk. Helyezzük a koordinátarendszer kezdőpontját a P0 pontszerű tárgynak a leképező rendszer által létrehozott P1 paraxiális képpontjába. A z-tengely legyen a kilépési pupillának a centrumától (C) a paraxiális képponton átmenő egyenes, és (y, z) sík legyen a meridionális sík. Ha az aberrációmentes hullámfronttal egybeeső R sugarú, origó középpontú ún. Gauss-féle referenciagömböt a kilépő fénysugár a Q pontban, míg a C ponton átmenő kilépő (aberrált) hullámfrontot a Qh pontban metszi, akkor a Φ aberrációfüggvény definíció szerint a QhQ előjeles távolság, mely pozitív, ha a QhQ irány megegyezik a fénysugarak irányával, negatív ellenkező esetben.

9.1. ábra. Az aberrációfüggvény a Gauss-féle referenciagömb és a kilépő hullámfront közötti távolság különbséget méri egy adott sugármentén.
Aberrációmentes esetben a kilépési pupillán áthaladó hullám egy (ideális) gömbhullám, így ekkor a Gauss-féle referenciagömbön a térerősség az
 |
(9.1) |
formulával írható le, ahol t az idő, A0/R a térerősség amplitúdója, c a fénysebesség és h(t) az impulzus időbeli alakját leíró függvény, amit a szokásos

alakban írunk fel, ahol b(t) az impulzus időbeli burkolója és ω0 a központi körfrekvencia. Az (9.1) kifejezésben az idő nullpontját úgy választottuk meg, hogy az impulzusfront a referenciagömbön a t = -R/c időpontban legyen. Az aberrációfüggvény definíciója alapján a Φ aberrációfüggvénnyel leírt aberráció jelenlétekor a referenciagömbön a térerősséget a
 |
(9.2) |
képlettel adhatjuk meg. Aberrációmentes esetnek nyilván a Φ = 0 felel meg. A referenciagömbön a fényimpulzust alkotó egyes monokromatikus összetevőket az (9.2) egyenlet Fourier-transzformálásával kapjuk:
 |
, |
ahol B(ω) a b(t) burkoló Fourier-transzformáltja, és k = ω/c a hullámszám. Az egyes monokromatikus összetevőkre a Seidel-féle aberrációk hatása a Nijboer-Zernike-féle elmélet segítségével tárgyalhatók [9.1]. Ez az elmélet pontosan a térerősség referenciagömbön felvett értékeinek az ismeretében adja meg a Gauss-féle képpont (itt az origó) környezetében lévő tetszőleges P pontbeli a térerősséget. Az [9.1] hivatkozás szerint a monokromatikus komponensek a

formulával adhatók meg, ahol
 |
, | (9.3) |
ahol

a P pont az előző fejezetben is látott "optikai" koordinátái, valamint z, r és ψ a P pont hengerkoordinátái, ahol a ψ szöget a szokásostól eltérően nem az x-tengelytől, hanem az y-tengelytől mérjük (9.2. ábra).

9.2. ábra. A számolásnál használt koordinátarendszer és a jelölések értelmezése
A meridionális síkot a ψ = 0 összefüggés adja meg. Az impulzus térerőssége a monokromatikus komponensek szuperpozíciójaként áll elő, azaz
 |
, | (9.4) |
ahol az inverz Fourier-transzformált kiszámításánál áttértünk a Δω = ω - ω0 integrálási változóra, amely az integrál numerikus kiszámításánál előnyös. A számolásoknál célszerű dimenziómentes változókra áttérni, mert ekkor egy adott numerikus számolás végeredménye több paramétercsoportra is vonatkozhat. Érdemes a távolságokat a központi hullámhosszhoz, az időt az ehhez tartozó periódusidőhöz viszonyítani. Vezessük be ezért a

dimenziómentes változókat, ahol λ0 = 2πc/ω0 a központi hullámhossz és T0 = 2π/ω0 a hozzátartozó periódusidő. A két mennyiség között nyilván a λ0 = cT0 összefüggés áll fenn. Ha az impulzus burkolóját a

alakban írjuk fel, akkor a dimenziómentes változókkal a (9.4) egyenlet az
 |
(9.5) |
formába írható át, ahol Ω = Δω/ω0 és S(ω) a s(t) függvény Fourier-transzformáltja. A későbbi számolásoknál feltesszük, hogy az impulzus burkolója egy Gauss-görbével írható le. Ezzel a feltételezéssel
 |
, |
amelynek a Fourier-transzformáltja
 |
. |
Célszerű az impulzus T időbeli hosszát is a T0 mennyiséghez viszonyítani, azaz T = NT0 alakba írni. Látható, hogy az N dimenziómentes mennyiség az impulzusban lévő optikai ciklusok számát adja meg. Ezekből már könnyen belátható, hogy a Gauss-féle időfüggésre
 |
. |
Az intenzitás a (9.5) egyenletből az I(P, t) = |E(P, t)|2 összefüggés felhasználásával számítható ki.
Látható, hogy a számolás egyik lényeges eleme a monokromatikus aberrációt helyfüggését leíró Y(u, v, ψ, Φ) függvény meghatározása egy adott Φ aberrációfüggvény esetén. A továbbiakban röviden először az ezzel kapcsolatos ismereteket tárgyaljuk, majd ennek birtokában megvizsgáljuk az egyes elsődleges aberrációknak az ultrarövid fényimpulzusokra gyakorolt hatását.
Elemi Seidel-féle aberrációk esetén az aberrációfüggvény
 |
(9.6) |
alakú [9.1], ahol n és m indexek értékeit az 9.1. táblázat mutatja az egyes elsődleges aberrációk eseteire. A számolásokhoz azonban az aberrációk Zernike-féle
 |
(9.7) |
alakját előnyös használni [9.1], ahol ![]() az n és m indexekhez tartozó radiális Zernike-polinom. Az aberrációk vizsgálatánál az aberrációfüggvényt sorba szokás fejteni [9.1], és a sorfejtésben az "elemi" tagok a (9.6) vagy (9.7) egyenletbeli Seidel- illetve Zernike-féle alakkal leírt elemi aberrációk [9.1].
az n és m indexekhez tartozó radiális Zernike-polinom. Az aberrációk vizsgálatánál az aberrációfüggvényt sorba szokás fejteni [9.1], és a sorfejtésben az "elemi" tagok a (9.6) vagy (9.7) egyenletbeli Seidel- illetve Zernike-féle alakkal leírt elemi aberrációk [9.1].
| Aberráció típusa | n | m |
|---|---|---|
| Szférikus | 4 | 0 |
| Kóma | 3 | 1 |
| Asztigmatizmus | 2 | 2 |
| Képmező görbület | 2 | 0 |
| Torzítás | 1 | 1 |
9.1. táblázat. Az aberrációfüggvény indexei elsődleges aberrációk esetén.
A kétféle - Φ és Φ' - aberrációkhoz tartozó (9.3) egyenletbeli Y függvények között az - [9.1] hivatkozásban bebizonyított - eltolási tétel adja meg a kapcsolatot.
A Nijboer és Zernike által kidolgozott eljárás [9.1] hivatkozásban leírt lépéseit követve megmutatható, hogy
 |
, | (9.8) |
ahol
 |
, | (9.9) |
 |
, | (9.10) |
Js az s-ed rendű Bessel-függvényt jelöli, továbbá
 |
. |
A (9.8) egyenletnél a belső összeget q olyan 0 és p közötti értékeire kell kiszámítani, amelyre q kongruens p-vel modulo 2, azaz p - q osztható 2-vel. Egyszerűbben fogalmazva a q összegző index a 0 és p közé eső páros vagy páratlan számokon fut végig, attól függően, hogy p páros vagy páratlan. A (9.9) formulákban lévő Dpq együttható definíciójában lévő zárójeles kifejezés a szokásos binomiális együtthatót jelöli, ahol a ' jelölés arra utal, hogy a q = 0 esetben a binomiális együtthatót még kettővel osztani kell. Érdemes megjegyezni, hogy mivel a Dpq együtthatókat a binomiális együtthatókból kapjuk, így azok a Pascal-féle háromszögből könnyen meghatározhatók.
A Nijboer és Zernike eljárásának a további fontos lépése a
 |
(9.11) |
sorfejtés. Ezt a sorfejtést a (9.10) integrálba helyettesítve,

Zernike-polinomok szorzatai jelennek meg, melyek biztosan kifejthetők
 |
(9.12) |
tipusú - Zernike-polinomok - lineáris kombinációjaként, ahol w = w(p, s, j) nem-negatív páros vagy páratlan szám, attól függően, hogy qm páros vagy páratlan. A (9.12) kifejtés A együtthatói és w(p, s, j) számok természetesen függenek az n és m értékeitől is, de ezt a függést nem jelöltük, mivel szeretnénk elkerülni az amúgy sem egyszerű jelölésrendszer tovább bonyolítását. A (9.12) előállítást felhasználva, a fellépő integrálok már analitikusan kifejezhetők a Bessel-függvényekkel [9.1], és így
 |
. | (9.13) |
A (9.12) kifejtés A együtthatóira nehéz zárt formulát találni [9.1], azonban a Zernike-polinomok tulajdonságait felhasználva az együtthatókra rekurziós összefüggéseket lehet levezetni. Ezek igen fontosak a p nagyobb értékeire történő számoláshoz, amely [9.1]-ben vizsgált aberrációknál nagyobb aberrációk kezeléséhez szükséges. A levezetések igen sok számolást igényelnek, ezért a részletekre nem kitérve, az egyes speciális aberrációkra vonatkozó végeredményt közöljük csak. Ezek az eredmények rendkívül fontosak a numerikus számolásoknál.
Elsődleges szférikus aberráció esetén n = 4 és m = 0. Ezért qm = 0, így (9.10) egyenletben a Bessel-függvény rendje q minden értékére 0. Ennek következtében az  integrál nem függ q-tól, így a továbbiakban q-t elhagyjuk a jelöléséből. Követve az [9.1] hivatkozásban leírt eljárást, a (9.12) kifejtés A együtthatóit az
integrál nem függ q-tól, így a továbbiakban q-t elhagyjuk a jelöléséből. Követve az [9.1] hivatkozásban leírt eljárást, a (9.12) kifejtés A együtthatóit az
 |
. |
formulák adják p = 0, 1 értékekre. A Zernike-polinomok tulajdonságait felhasználva, hosszú számolással megmutatható, hogy adott p esetén a j összegző index olyan értékeken fut végig melyre a

mellékfeltételek állnak fenn. Továbbá, amennyiben megállapodunk abban, hogy
 |
, |
akkor a p = 2, 3, 4, ... értékekre az
 |
(9.14) |
rekurziós összefüggés áll fenn, ahol k = 0, 1, 2, 3, ..., 2p. Ez rekurzió a fent említett rekurziónak a speciális esete. A (9.12) kifejtésben megjelenő w(p, s, j) szférikus aberráció esetén
 |
. |
Mindezeket figyelembe véve a (9.10) és (9.13) egyenletek alakja erre a speciális esetre
 |
. |
Mivel m = 0, így (-i) qm cos(qmψ) = 1. A binomiális együtthatók tulajdonságait kihasználva, (9.8) egyenlet erre a speciális esetre az
 |
(9.15) |
képletre vezet. Látható, hogy a Y valójában nem függ a ψ szögtől, amely a szférikus aberrációnál nyilván meglévő hengerszimmetriát fejezi ki. A már említett eltolási tétel [9.1] felhasználásával, a - (9.6) egyenlettel adott - Seidel-féle formára az
 |
(9.16) |
összefüggést kapjuk, ahol a (9.7) képletbe a

mennyiséget kell behelyettesíteni!
A (9.12) kifejtés A együtthatóit az

összefüggések adják a p = 0, 1, 2 értékekre, ahol r = 2s. A vektorok sorainak fentről lefelé rendre a j = 0, 1, 2, ... értékek felelnek meg. Adott p esetén a j összegző index olyan értékeket vesz fel, amelyre a

mellékfeltételek állnak fenn. Továbbá, amennyiben megállapodunk abban, hogy
 |
, |
akkor a p = 3, 4, ... értékekre az
 |
(9.17) |
rekurziós összefüggések állnak fenn, ahol k = 0, 1, 2, 3, ..., 2p és
 |
. |
A (9.12) kifejtésben megjelenő w(p, s, j) asztigmatizmus esetén
 |
. |
Mindezeket figyelembe véve a (9.10) és (9.13) egyenletek alakja erre az aberrációra
 |
, |
továbbá (9.8) egyenlet az

alakot veszi fel. Az eltolási tétel [9.1] felhasználásával, a - (9.6) egyenlettel adott - Seidel-féle formára
 |
, |
ahol a (9.7) képletbe a

mennyiséget kell behelyettesíteni.
A (9.12) kifejtés A együtthatóit az

összefüggések adják a p = 0, 1, 2 értékekre, ahol r = 2s. A vektorok sorainak - itt is - fentről lefelé rendre a j = 0, 1, 2, ... értékek felelnek meg. Adott p esetén a j összegző index olyan értékeken fut végig, amelyre a

mellékfeltételek állnak fenn. Továbbá, amennyiben most is megállapodunk abban, hogy
 |
, |
akkor a p = 3, 4, ... értékekre az
 |
. | (9.18) |
rekurziós összefüggések állnak fenn, ahol k = 0, 1, 2, 3, ..., 2p és
 |
. |
A (9.12) kifejtésben megjelenő w(p, s, j) kóma esetén
 |
. |
Mindezeket figyelembe véve a (9.10) és (9.13) egyenletek alakja erre az aberrációra
 |
, |
továbbá (9.8) egyenlet az

formába írható. Az eltolási tétel [9.1] felhasználásával, a - (9.6) egyenlettel adott - Seidel-féle formára
 |
, |
ahol itt az (u, v, ψ) koordináták helyett az (x, y, z) Decartes-féle koordinátákat használtuk, mivel az eltolás ezekkel könnyebben kifejezhető. Kóma esetén (9.7) képletbe a

mennyiséget kell behelyettesíteni.
Az n = 2, m = 0 eset gyakorlatilag visszavezethető az aberrációmentes esetre. Az eltolási tétel [9.1] segítségével megmutatható, hogy
 |
. |
Az u változó definíciója alapján, ez az összefüggés az aberrációmentes eset térerősségének a z-tengely menti Δz = 2(R/a)2A20 -lal történő eltolását jelenti.
Az n = 1, m = 1 eset szintén visszavezethető az aberrációmentes esetre, mert az eltolási tétel [9.1] segítségével megmutatható, hogy
 |
, |
ahol itt is az (u, v, ψ) koordináták helyett az (x, y, z) használta célszerű, mert ezekkel egyszerűbb leírni az eltolást. Nyilvánvaló, hogy az összefüggés az aberrációmentes eset térerősségének az y-tengely menti Δy = (R/a) A11 -gyel történő eltolását jelenti.
A hullámfront ismeretében a geometriai optika fénysugarai meghatározhatók, ugyanis ismert, hogy homogén és izotróp közegben a fénysugarak a hullámfelületre merőleges egyenesek és az adott fénysugár mentén a fény c sebességgel terjed. Az (r, φ, ε) gömbi koordinátákat használva, az aberrált hullámfrontot az
 |
(9.19) |
formula írja le (9.2. ábra), ahol a Φ aberrációfüggvényt a (ρ, θ) változók helyett a (ε ,φ) polár- és azimut szögekkel fejeztük ki. A változókat a

összefüggések kapcsolják össze. Ha bevezetjük az
 |
(9.20) |
függvényt, akkor (9.19) egyenlet alapján az aberrált hullámfront egyenletét a

időpontban az

egyenlet határozza meg. A fénysugarak irányát az S függvény gradiensének segítségével határozhatjuk meg, mivel a gradiens merőleges a felületre. Ennek megfelelően a fény terjedési irányába mutató vektor
 |
, |
ahol er, eφ, eε a gömbi koordinátarendszer bázisvektorai. A (9.19) és a (9.20) egyenleteket felhasználva
 |
. |
Az er, eφ, eε bázisvektorokat a Descartes-féle derékszögű koordinátarendszer ex, ey, ez bázisvektoraival kifejezve az
 |
. | (9.21) |
kifejezést kapjuk. Az aberrált hullámfront (Qh-val jelölt) pontjait derékszögű koordinátarendszerben az

egyenlettel fejezhetjük ki. Mivel a fény egy adott sugár mentén c sebességgel terjed, a hullámfront egyenlete a t időpontban
 |
, |
ahol
 |
. |
Ha bevezetjük a t0 időpontot a
 |
(9.22) |
definícióval, akkor a hullámfront egyenletét az
 |
. | (9.23) |
alakban is felírhatjuk, ahol
 |
. | (9.24) |
A későbbi számolásokból látni fogjuk, hogy Φ « R esetén s ≈ 1, és így ct0 ≈ Φ (lásd a (9.27), (9.31) és a (9.34) egyenleteket).
Az aberrációfüggvény Seidel-féle - (9.6) egyenletbeli alakja - az (ε, φ), illetve az (α, θ) (9.2. ábra) szögekkel a

formába írható át, ahol
 |
. |
A következő alfejezetekben a (9.21) és a (9.24) egyenleteknek az egyes elsődleges aberrációkra vonatkozó alakját ismertetjük.
A hengerszimmetria miatt elegendő a sugarakat egy a z-tengelyt tartalmazó síkban vizsgálni, továbbá a Φ = Φ40 aberrációfüggvény φ szerinti deriváltja nulla. Ha sugarakat a meridionális síkban (vagyis az ex, ey vektorok által kifeszített síkban) vizsgáljuk (azaz φ = π/2 és θ = 0), a lehetséges egyszerűsítések után, a (9.21) és a (9.24) egyenletek az
 |
(9.25) |
és az
 |
. | (9.26) |
formába írhatók át. Továbbá a t0 időpontot meghatározó (9.22) egyenletre sorfejtéssel a
 |
(9.27) |
közelítést kapjuk.
A nyílást kitöltő hullámfrontból a gyújtófelület (kausztika) egyenlete is meghatározható. A részleteket mellőzve, a kausztikát a (z, y) síkban (θ = 0) - a λ « R és Φ40 « R feltételek teljesülése esetén - a
 |
. | (9.28) |
paraméteres görbe írja le, ahol a két utolsó közelítés paraxiális közelítés eredménye. A térbeli gyújtófelület a (9.28) egyenletben adott görbének a z-tengely körüli forgatásával adódik.
A Φ = Φ22 aberrációfüggvény deriváltjainak a kiszámításával, és a lehetséges egyszerűsítések elvégzésével a (9.21) és a (9.24) egyenletek az
 |
(9.29) |
és az
 |
(9.30) |
formába írhatók át. Továbbá a t0 időpontot meghatározó (9.22) egyenletre sorfejtéssel a
 |
. | (9.31) |
közelítést kapjuk.
Kromatikus aberráció hiányában (pl. tükrök esetén) az impulzus monokromatikus összetevőinek a fázissebessége azonos, így az összetevők fázisfontjainak az eltérése a referenciagömbtől minden összetevőre azonos. Ami azt jelenti, hogy Φ nem függ a frekvenciától. Az aberrációfüggvény a hullámfront eltérését méri az ideális gömb alaktól. Ebből is rögtön látszik, hogy a (9.6) egyenletben fellépő - hosszúság dimenziójú - Anm állandót célszerű az impulzus központi hullámhosszához viszonyítani, vagyis az

alakba formába írni, ahol μ nm dimenziómentes állandó.
A következő alfejezetekben a (9.5) egyenletből számolt intenzitáseloszlásokat mutatjuk be. A beeső impulzus időbeli lefutásáról feltételezzük, hogy Gauss-görbével írható le. Feltesszük még, hogy az impulzus mindössze 2 optikai ciklusból áll (N = 2), vagyis az igen rövid. Titán-zafir lézer esetén (λ0 = 800 nm, T0 = 2.67 fs) az N = 2 választás T = 5.34 fs időbeli hosszat jelent. A hullámoptikai számítások eredményeit összehasonlítjuk majd a geometriai optika által jósolt impulzusfronttal. A (9.23) egyenlet szerint egy adott t időpontban az impulzusfrontot az (ε, φ) (vagy helyettük a (α, θ)) paraméterekkel generált

felület adja meg. Ennek a felületnek és az optikai tengelyt tartalmazó, a meridionális síkkal ψ szöget bezáró síknak a közös pontjait, vagyis a ψ paraméterrel adott síkbeli impulzusfrontot a

egyenlet megoldásával nyerjük. Az hullám- és geometriai optikai számítások összehasonlításnál az I intenzitás értékhez egy Sz szürkeségi szintet rendelünk, az Sz = C I 1/3 összefüggés szerint, ahol a C állandót úgy választottuk meg, hogy a maximumnak a (teljesen) fehér szín feleljen meg. A számításokat a numerikus apertúra a/R = 0.1 értékére végeztük el.
Mivel az Anm állandó nem függ a frekvenciától a képmező görbület esetén a
|
Δz = 2(R/a)2A20 = 2(R/a)2 μ20 λ0 |
eltolás szintén független frekvenciától, azaz minden monokromatikus összetevőre azonos. Ennek következtében az képmező görbület nem okoz tér- és időbeli torzulást. Hatására mindössze az aberrációmentes esethez tartozó térerősség Δz -vel eltolódik a z-tengely mentén. Teljesen hasonlóan belátható, hogy a torzítás sem vezet be tér és időbeli torzulást. Hatása az aberrációmentes térerősségnek az y-tengely mentén
|
Δy = (R/a) A11 = (R/a) μ11 λ0 |
mennyiséggel való eltolásában mutatkozik meg.
A szférikus aberráció hatását a μ40 = -6 esetén szemléltetjük. Ez azt jelenti, hogy az ideális gömbfelülettől a legnagyobb eltérés 6λ0 (a nyílás szélénél), továbbá μ40 < 0 miatt hullámfront kissé görbültebb, mint az aberrációmentes esetben. Ennek következtében a marginális sugarak a fókusznál (a nyíláshoz viszonyítva) közelebb metszik az optikai tengelyt. A szemléltetéshez a τ = t/T0 = -7000, -2394, -1800 és 500 időpontokat választottuk. Az első időpontnál az impulzus a marginális fókuszpont előtt, az utolsónál a paraxiális fókuszpont után, míg a két közbülső időpontnál a marginális és a paraxiális fókuszpontok közötti tartományban helyezkedik el. A számítások eredményeit a 9.3. ábra szemlélteti. Egy sík-domború lencse által létrehozott szférikus aberrációnak egy 24 fs-os impulzusra gyakorolt hatását a mellékelt animáció szemlélteti [8.11].

9.3. ábra. Két optikai ciklust (T = 2T0) tartalmazó rövid fényimpulzus intenzitáseloszlása a t = -7000T0, -2394T0, -1800T0 és a 500T0 időpontokban a μ40 = -6 paraméterrel adott első rendű szférikus aberráció jelenlétekor. A szürke szaggatott vonal a geometria optika által jósolt impulzusfrontot, míg a folytonos vonal a kausztikát jelöli.
A 9.3. ábrán a hullám- és a geometriai optikai számítások eredményeit is összehasonlítottuk. A szürke szaggatott vonal a geometria optika által jósolt impulzus-frontot, a szürke folytonos vonal a kausztikát szemlélteti. A 9.3. (a) és (d) részén jól látható, hogy az aberrációmentes esethez hasonlóan itt is megjelenik az előző fejezetben már tárgyalt szélihullám-impulzus [9.2, 9.3, 9.4, 9.5, 9.6], amelyet a nyílás pereméről kiinduló elemi hullámok interferenciája hoz létre.
Aberrációmentes esetben a széli-hullám-impulzus helyét a

egyenlet határozza meg. Könnyen belátható, hogy a most vizsgált szférikus aberráció jelenlétekor a szélihullám-impulzus helyzetét az optikai tengelyen a

egyenletből számíthatjuk ki. A szélihullám-impulzus teljes mértékben hullámoptikai jelenség, jelenléte a geometriai optikával nem magyarázható. Az ábrákról láthatjuk, hogy az impulzusfront alakját viszont a geometriai optika igen jól visszaadja. A számítások azt mutatják, hogy a szférikus aberráció következtében számottevő időbeli kiszélesedés nem lép fel, azonban az aberráció jelentős hatással van az impulzus térbeli alakjára, továbbá a jelentősen csökkenti az elérhető maximális intenzitást.
Megmutatható, hogy a hullámfelület ρa sugarú körön lévő pontjaiból kiinduló sugarak a

koordinátájú pontban metszik az optikai tengelyt (0 ≤ ρ ≤ 1). A 9.3. (b) ábrán a nyílás széléről érkező sugarak (ρ = 1) mentén a fényimpulzus éppen eléri az optikai tengelyt, azaz éppen a marginális fókuszponton halad keresztül (z1/λ0 = -2400). Kisebb ρ értékhez tartozó sugarak az optikai tengelyt az origóhoz közelebbi pontban metszik. Ezen sugarak mentén a fényimpulzus a tengelyt a 9.3. (b) ábrának megfelelő időpontnál későbbi időpontban éri el, míg a szélső sugarak mentén érkező fény már elhagyta a tengelyt, ahogy ez a 9.3. (c) ábrán is látható. Az impulzusfront ezen furcsa befűződését a marginális és a paraxiális fókuszpontok közötti tartományban figyelhetjük meg. A tengelyhez közeli sugarak mentén terjedő fény közel gömbi impulzusfrontot hoz létre.
A radiális intenzitáseloszlás mellékmaximumai nagyobbak, mint az aberrációmentes esetben fellépő Airy-féle eloszlás mellékmaximuma. A részletesebb vizsgálat azt mutatja, hogy a radiális eloszlás a szélihullám-impulzus eloszlásához hasonló [9.2, 9.4] (azaz a J02 függvénnyel közelíthető). Ez a viselkedés tulajdonképpen nem meglepő, hiszen a szélihullámokhoz hasonlóan itt is olyan interferenciajelenséggel van dolgunk, amikor a fény terjedési iránya egy olyan kúpnak a palástjára esik, amelynek a tengelye az optikai tengely.
Az asztigmatizmus hatásának bemutatásához a μ22 = 1.5 értéket választottuk. A meridionális, vagyis az (y, z) síkban (ψ = 0ş) lévő fókuszvonal az optikai tengelyen zm = 0 helyen, míg a meridionális síkra merőleges (z, x), azaz a szagittális síkban (ψ = 90ş) lévő fókuszvonal a
|
zs = 2 A22 (R/a)2 = 2 μ22 λ0 (R/a)2 |
helyen helyezkedik el, amely a számolásbeli paraméterekkel zs = 300 λ0. A szemléltetéshez a τ = t/T0 = -2000, 0,150, 300 és 2000 időpontokat választottuk. Ezekben az időpontnál az impulzus rendre a meridionális fókuszvonal előtt, a meridionális fókuszvonalnál, a két fókuszvonal között, a szagittális fókuszvonalnál és a szagittális fókuszvonal után helyezkedik el. Az intenzitás szemléltetésére az előző esetben használt intenzitás - szürkeség megfeleltetést használtuk. A geometriai optikából kapott impulzusfrontot itt szintén szaggatott vonal szemlélteti. Mivel az intenzitáseloszlás már nem hengerszimmetrikus, az intenzitást a meridionális síkkal ψ = 0ş és 90ş szögeket bezáró - az optikai tengelyt tartalmazó - síkokban szemléltettük. A Φ22 szimmetria tulajdonságaiból következik, hogy az intenzitás eloszlása szimmetrikus mind az (y, z), mind a (z, x) síkokra. Az egyes időpontokra vonatkozó számolási eredményeket rendre a 9.4. ábra mutatja.

9.4. ábra. Két optikai ciklust (T = 2T0) tartalmazó rövid fényimpulzus intenzitáseloszlása a t = -2000T0 , 0, 150T0, 300T0 és 2000T0 időpontban A22 = 1.5 λ0 paraméterrel adott asztigmatizmus jelenlétekor a meridionális síkhoz képest ψ = 0 és 90° szöget bezáró, a z-tengelyt tartalmazó síkban. A szürke szaggatott vonal a geometria optika által jósolt impulzusfrontot jelöli.
Látható, hogy a szélihullám-impulzus asztigmatizmus jelenlétében is megmutatkozik (9.4. ábra (a) és (e) része), a hengerszimmetria megszűnése ellenére. Azonban az aberráció hatására a szélihullám-impulzus térbeli tulajdonságai megváltoznak. Például a nem tengelyen lévő maximumok jelentősen megnőnek. Az ábrák azt is mutatják, hogy a geometriai optika a fókuszvonalaktól eltekintve igen jól megadja az impulzus térbeli alakját. A geometriai optikai leírás a meridionális fókuszvonalnál csak a meridionális síkban (9.4. ábra (b) rész), míg a szagittális fókuszvonalnál csak a szagittális síkban (9.4. ábra (d) rész) vezet megfelelő eredményre.
A kóma hatását a μ31 = 2.5 paraméterrel szemléltettük. Kóma esetén az intenzitáseloszlás szimmetriája tovább csökken, A Φ31 szimmetria tulajdonságaiból megmutatható, hogy az intenzitás eloszlása már csak az (y, z), azaz a meridionális síkra szimmetrikus. A szemléltetéshez a τ = t/T0 = -2000, -200, 0, 200 és 2000 időpontokat választottuk. Az egyes időpontokra vonatkozó számolási eredményeket rendre a 9.5. ábra mutatja. Az intenzitást - minden időpontra - a meridionális síkkal ψ = 0ş és 90ş szögeket bezáró síkokban szemléltettük. A geometriai optikából kapott impulzusfrontot itt is a szaggatott vonal mutatja.

9.5. ábra. Két optikai ciklust (T = 2T0) tartalmazó rövid fényimpulzus intenzitáseloszlása a t = -2000T0, -200T0, 0, 200T0 és a 2000T0 időpontban A31 = 2.5 λ0 paraméterrel adott kóma jelenlétekor a meridionális síkhoz képest ψ = 0 és 90° szöget bezáró, a z-tengelyt tartalmazó síkban. A szürke szaggatott vonal a geometria optika által jósolt impulzusfrontot jelöli.
Amint az ismeretes [9.1], a kóma hatására, a z = 0 (kép)síkban az y > 0 és -30ş≤ ψ ≤ 30ş tartományban szóródnak szét a fénysugarak, elmosva ezzel a képet. Ennek megfelelően érthető, hogy a képsíkhoz közel az impulzusfront az y > 0 tartományba tolódik át, mint ahogy ez a 9.5. ábrán látható. Azokon helyeken, melyek geometriai optikai értelemben a megvilágított tartományban vannak és nincsenek túl közel az árnyék határához (geometriai elmosódottság határához), a geometriai optikai modell jól visszaadja az impulzusfront alakját.
A szimmetriatulajdonságok további romlásának ellenére a szélihullám-impulzus kóma esetén is megjelenik, az aberrációmentes esethez képest megváltozott tér- és időbeli tulajdonságokkal (9.5. ábra). A térbeli alakja a meridionális síkban hasonlít leginkább az aberrációmentes esetre, bár jól látható, hogy eltolódik az y > 0 tartományba, vagyis nem a z-tengelyen terjed. A szagittális síkban csak a jellegzetes X alak marad meg, a minimumok és maximumok keresztirányú váltakozása eltűnik
Értelmezze az aberrációfüggvényt!
Ismertesse a monkormatikus aberrációk típusait! Adja meg az ezeket jellemző aberrációfüggvényeket elsődleges aberrációk esetén.
Az elsődleges aberrációkat leíró aberrációfüggvényeket vizsgálva állapítsa meg az egyes aberrációk szimmetriatulajdonságait!
Vezesse le szférikus aberráció gyújtófelületét meghatározó (9.28) egyenleteket!
[9.1] M. Born and E. Wolf, Principles of Optics, (Cambridge University Press, 7th edition), chapter IX.
[9.2] Zs. Bor, Z. L. Horváth, Distortion of Femtosecond Pulse in Lenses. Wave Optical Description Optics Commun. 94 (1992) 249.
[9.3] Z. L. Horváth, Zs. Bor, Behaviour of Femtosecond Pulses on The Optical Axis of a Lens. Analytical Description, Optics Commun. 108 (1994) 333.
[9.4] Z. L. Horváth and Zs. Bor, Diffraction of short pulses with boundary wave theory, Phys. Rev. E 63 (2001) 26601.
[9.5] Z. L. Horváth, J. Klebniczki, G. Kurdi and A. P. Kovács, Experimental investigation of boundary wave pulse, Optics Commun.239 (2004) 243.
[9.6] P. Saari, P. Bowlan, H. Valtna-Lukner, M. Löhmus, P. Piksarv and R. Trebino, Basicdiffraction phenomena in time domain, Opt. Express 18 (2010) 11083-8.
Tartalom
A 4. fejezetben már megmutattuk, hogyha egy rövid fényimpulzus diszperzív optikai elemen keresztülhalad (pl. üveglemezen), akkor az időbeli alakja megváltozik. Ennek oka, hogy az optikai elem az impulzust alkotó különböző frekvenciájú spektrális komponensek fázisát különböző mértékben eltolja. Ennek kapcsán kétféle mérés igénye merül fel, az egyik az optikai elem spektrális fázisfüggvényének, míg a másik az impulzus időbeli alakjának mérése. Ez utóbbira kifejlesztett mérési módszereket a 12. fejezetben tekintjük át.
Az optikai elemek spektrális fázisfüggvényének mérésére rendszerint lineáris interferometrikus technikákat használunk, azaz a mérőeszköz detektora a beérkező fény intenzitásával arányos elektromos jelet ad ki. A lineáris detektálási technika előnye a nemlineáris technikával szemben a nagyobb érzékenység. A lineáris módszerek közös jellemzője, hogy a vizsgálat tárgyát képező optikai elemet egy kétutas interferométer egyik karjában (a tárgykarban) helyezzük el, míg a másik kar referenciaként szolgál (10.1 ábra).

Az interferométert vagy széles spektrumú fényforrással (pl. halogénlámpa, LED, Ti:zafír lézer, Ti: zafír kristály erősített spontán emissziója, fehérfény-kontinuum), vagy széles hullámhossz-tartományban hangolható fényforrással (pl. hangolható festéklézer, optikai parametrikus oszcillátor) világítjuk meg. Az interferométer kimenetén egy lineáris detektort helyezünk el. A detektor típusától függően további két csoportra bonthatók a mérési módszerek, idő- illetve frekvenciatartománybeli módszerekre. Előbbi esetében fotodiódát vagy fotoelektronsokszorozót használunk, míg az utóbbi esetben diódasort vagy CCD chipet egy spektrográf kimenetén elhelyezve.
A módszerek alkalmazhatósága szempontjából fontos figyelnünk arra, hogy egylövéses vagy többlövéses a módszer. Az egylövéses módszer annyit jelent, hogy egyetlen méréssel kapott interferogramból már a spektrális fázisfüggvény meghatározható. Ide tartozik az összes, spektrális bontásra épülő (azaz a frekvenciatartománybeli) módszer. Az időtartománybeli módszerek esetében viszont több, különböző késleltetésnél mérjük meg az interferométer kimenetén a jelet, amiből aztán visszaszámoljuk a spektrális fázisfüggvényt. Ebből következőleg ezek a módszerek a többlövéses módszerek közé tartoznak. Először tekintsük át az időtartománybeli mérési módszereket.
Ebben az esetben az interferométer kimentén egy lineáris, kicsiny fényérzékelő felülettel rendelkező fotodetektort (pl. fotodiódát) helyezünk el, és az interferométer referenciakarjában lévő késleltető elem tükrét időben közel állandó sebességgel mozgatjuk előre-hátra a zérus karhosszkülönbséghez tartozó pozíció körül. A kimeneten a referencia- és a tárgynyaláb interferenciájaként kialakuló fényintenzitást folyamatosan regisztráljuk. Vizsgáljuk meg, hogy hogyan határozható meg a kapott interferogramból a mérendő diszperzív minta φ m (ω) spektrális fázisfüggvénye [10.1].
Az interferométerbe belépő fénynyaláb spektrális fényintenzitását jelöljük I(ω)-val, míg a spektrális fázisát φ f (ω)-val. Az interferométer bemeneténél (z=0) a fényhullám térerőssége:
 |
(10.1) |
Az interferométer referencia- illetve tárgykarjában a fény zR illetve zT utat tesz meg a levegőben, azaz a geometriai úthossz-különbség Δz=zT-zR. Az interferométer nyalábosztóin való keresztülhaladáskor illetve a tükrein való visszaverődéskor változhat a fényhullám spektrális intenzitása és spektrális fázisa is. Ezt a komplex reflexiós tényezővel vesszük figyelembe:
 |
(10.2) |
ahol φ Ro (ω) a referenciakarban, míg φ To (ω) a tárgykarban lévő optikai elemek eredő spektrális fázisfüggvényét jelöli. Fontos megjegyezni, hogy ez utóbbi mennyiségbe a mérendő diszperzív minta φ m (ω) spektrális fázisát nem értettük bele. Az interferométer kimenetén a referencia- illetve a tárgykarból érkező fényhullámok térerőssége:
 |
(10.3) |
ahol c a vákuumbeli fénysebességet jelöli, és a levegő törésmutatóját 1-nek vettük.
A detektornál a két nyaláb térerőssége koherens módon adódik össze, azaz a detektor a két karból egymáshoz képest időbeli késéssel érkező fényhullámok térerősségének összegét érzékeli
 |
(10.4) |
Mivel a fényhullámok periódusideje néhány femtoszekundum, így a detektor csak az intenzitás időbeli átlagát képes mérni, azaz
 |
(10.5) |
A (10.4) egyenletet (10.5) integrandusába beírva kapjuk, hogy
 |
(10.6) |
Az egyenlet jobb oldalának első és második tagját idő szerint kiintegrálva egy-egy állandó értéket kapunk. A minta fázistolásáról a harmadik és negyedik tag, azaz a keresztkorrelációs tagok hordozzák az információt. Figyelembe véve, hogy az <exp(iω1t-iω2t)>=Δ(ω1-ω2), ahol <> jelek az időbeli átlagolást jelölik, így a keresztkorrelációs jelre adódik, hogy
 |
(10.7) |
ahol τ=Δz/c a tárgynyalábnak a referencianyalábhoz képesti, az eltérő geometriai úthossztól származó időbeli késése. Vegyük észre, hogy az egyenletben már nem szerepel az interferométerbe belépő fénynyaláb φ f spektrális fázisfüggvénye, azaz a detektált jel csak az interferométer két karja közötti fáziskülönbségtől függ. Ebből következik, hogy alapvetően mindegy, hogy egy közönséges fehér lámpát használunk fényforrásként, ahol a spektrális komponensek fázisa egymáshoz képest véletlenszerűen változik, vagy éppen egy drága femtoszekundumos lézert, ahol viszont a komponensek fázisa egymáshoz képest rögzített. A lézer jó kollimáltsága és jó térbeli koherenciája azonban a mérést jóval könnyebbé teszi, mintha csak egy halogén lámpát használnánk. Vegyük észre azt is, hogy detektor jelét nemcsak a diszperzív minta, hanem a referencia- és tárgykar optikai elemeinek spektrális fázisfüggvénye is befolyásolja.
Ezek után vizsgáljuk meg, hogy hogyan változik a detektor jele, ha diszperzív mintát helyezünk a tárgykarba. Ahhoz, hogy ezt megfigyelhessük, először tekintsük azt az esetet, amikor az interferométer üres, azaz nincs diszperzív elem egyik karjában sem, és egy 6 fs-os, 800 nm központi hullámhosszú transzformlimitált lézerimpulzussal világítjuk meg (10.2. ábra). A késleltető elemmel változtassuk az interferométer két karjából érkező impulzusok között a τ időbeli késleltetést, és a 10.2. ábrához tartozó animáción figyeljük meg, hogyan változik a dióda jele.

10.2. ábra. a) Az interferométerből kilépő, egymáshoz képest időben késleltetett lézerimpulzusok térerőssége. b) A fotodióda által detektált jel a késleltetés függvényében.
Láthatjuk, hogy amikor a két impulzus időben nem fed át, akkor a késleltetés értékétől nem függ a dióda által detektál jel, végig egy állandó értéket mutat. Azonban amikor a két impulzus elkezdi időben átfedni egymást, az interferencia eredményeképpen a dióda jele az átfedés nélküli esetben kapott értéknél nagyobb illetve kisebb is lehet. A jel időbeli periódusa megegyezik a fényimpulzus periódusidejével (jelen esetben T=2,7 fs), mivel erősítés akkor lehet csak, ha a két impulzusnak a térerősség maximumai egymásra esnek. A detektor jele a maximális értéket akkor éri el, amikor a két impulzus közötti időbeli késleltetés zérus. Vegyük észre, hogy eléggé hasonló a detektor által mért ún. keresztkorrelációs jel alakja az impulzusok térerősségéhez, a periódusa is azonos időtartamú. Azonban fontos különbség, hogy míg az impulzusok térerősségénél a vízszintes tengely az időtengely, addig a keresztkorrelációs jelnél egy idő dimenziójú mennyiség szerepel, a két kar közötti időkésés. Ezért bár ezen a tengelyen is femtoszekundumos időskálát látunk, itt egy-egy mérési pont egy adott karhosszkülönbséghez, azaz egy adott késleltetéshez tartozik. Így érdekes módon bár a legjobb detektorok is csak pikoszekundumos integrálási idővel tudnak mérni, mégis femtoszekundumos időskálán történő változásokról is kaphatunk információt az interferencia jelenségének segítségével.
A repülésiidő-interferometria azon az előbb említett tényen alapul, hogy a detektor jele a maximális értéket akkor éri el, amikor az interferométer két karjából érkező impulzus közötti időbeli késleltetés zérus. Ennél a technikánál az interferométert megvilágító fényforrásnak kvázimonokromatikusnak kell lenni, azaz pl. egy sávszűrővel ellátott fehér lámpa [10.2] vagy egy hangolható festéklézer [10.3] használható e célra. Az interferométer optikai elemeinek, valamint a vizsgálandó diszperzív mintának a rajta keresztülhaladó kvázimonokromatikus fényre gyakorolt hatásának leírásánál a kis spektrális sávszélesség miatt elegendő, ha a spektrális fázisfüggvényeknek a Taylor-sorát csak első rendig vesszük figyelembe. Ezt felhasználva a (10.7) egyenletet az alábbi alakra írhatjuk át
 |
(10.8) |
ahol ω0 a kvázimonokromatikus fény központi frekvenciája. A (10.8) egyenletből látható, hogy a mért interferenciajel maximuma a tárgykar és a referenciakar csoportkésleltetés különbségének függvényében eltolódik. Így a vizsgált optikai elem csoportkésleltetés-függvényét úgy kaphatjuk meg, hogy egy adott ω0 frekvenciánál a kapott interferogram (keresztkorrelációs jel) maximális láthatóságához tartozó késleltetést meghatározzuk. Az interferogram V láthatóságát egy adott időpillantban a V=(Imax-Imin)/(Imax+Imin) összefüggés alapján tudjuk meghatározni, ahol Imax és Imin az adott időpillanathoz legközelebb eső interferenciacsúcs illetve -völgy intenzitásértéke. Majd megváltoztatjuk a kvázimonokromatikus fény ω0 körfrekvenciájának értékét, és ismét megkeressük a láthatósági-maximumhoz tartozó késleltetés értékét. Ezt megismételjük több különböző körfrekvencia értéknél. Ily módon a relatív csoportkésleltetés közvetlenül a láthatósági maximumok helyéből meghatározható. A repülésiidő-interferometriának a legnagyobb előnye épp ebben, a csoportkésleltetés közvetlen mérési lehetőségében van.

10.3. ábra. a) Három különböző hullámhossz esetében a referencia impulzus és az 5 mm kvarc lemezen áthaladt tárgyimpulzus térerőssége a referenciaimpulzus adott késleltetésénél. b) A fenti ábrának megfelelő keresztkorrelációs jelek.
A 10.3. ábrán egy szimulált pillanatfelvételt láthatunk három hullámhosszra, 700 nm-re (kék vonal), 800 nm-re (zöld vonal) és 900 nm-re (piros vonal) vonatkozóan. A különböző hullámhosszú referenciaimpulzusokkal miközben egy szkennelést végzünk, azaz a referenciakar hosszának változtatásával változik τ is (lásd animáció), az alsó ábrán látható keresztkorrelációs jeleket kapjuk. Mivel a kvarclemezben a hosszabb hullámhosszú komponensek gyorsabban terjednek, mint a rövidebb hullámhosszúak, így a referenciaimpulzus szkennelésekor a hosszabb hullámhossznál előbb jelenik meg a keresztkorrelációs jel, mint a rövidebb hullámhosszúénál.
Ügyelni kell a mérésnél arra, hogy az üres interferométer két karjában is lehet diszperziót okozó optikai elem, ezért először az üres interferométer két karja közötti maradék diszperzió okozta φ' To -φ' Ro csoportkésleltetést kell megmérnünk. Csak ezután helyezzük be a diszperzív mintát, és végezzük el újra a mérést. A két mért függvény különbsége adja a minta φ' m csoportkésleltetés-függvényét. Vegyük észre, hogy a τ pontos értékét nem ismerjük, így csak a minta relatív csoportkésleltetés-függvényét tudjuk megmérni.
A mérések kivitelezésekor az egyik probléma a mérés időbeli és spektrális felbontásának kapcsolata. Minél nagyobb a fényforrás sávszélessége, annál rövidebb tartományon láthatók csak interferenciacsíkok, azaz annál pontosabban lehet meghatározni a láthatósági maximum helyét és így a csoportkésleltetést. Azonban ekkor a spektrális felbontás romlik. A másik probléma, hogy ha a spektrális fázisfüggvényt minél több hullámhosszon szeretnénk meghatározni, akkor a mérés eléggé hosszadalmassá válik, mivel minden egyes hullámhosszon külön-külön kell a mérést végrehajtani. Ez a fél órát is elérheti, ami viszont azt eredményezi, hogy a termikus hatások miatt a mérések során a karhosszak változhatnak, ezért szükséges ezt folyamatosan ellenőrizni, pl. egy He-Ne lézer nyalábjával. További probléma a láthatósági maximum helyének pontos meghatározása. Mivel a detektált Ikorr(τ) függvényen két lokális intenzitásmaximum közötti időkülönbség kb. a fényhullám periódusideje, így ahhoz hogy legalább néhány mérési pont essen két maximum közé, a referencia tükör λ/8 mértékű mozgatására van szükség. Ez csak igen drága eltolóval oldható meg, melynek a mozgatásához egy léptetőmotorra is szükség van. A detektált intenzitásgörbére általában jelentős zaj is rárakódik. A ±1 fs időbeli felbontás eléréséhez a zaj kiküszöbölésére Knox és munkatársai lock-in erősítőt használtak, és a fényforrás fényét 1 kHz-cel szaggatták [10.2]. A kapott intenzitásgörbéből csak számítógépes adatfeldolgozással tudták meghatározni a láthatósági maximumot, mivel még 45 nm-es léptetés esetén sem kaptak elég sima intenzitás-késleltetés görbét. Tükrök vizsgálata esetén többszörös reflexiók használatával növelték meg az időbeli felbontást. 12-szeres reflexióval ±1/12 fs-os időbeli felbontást értek el. Itt azért megjegyezzük, hogy ha kisebb pontosság (±30 fs) is elég, akkor az imént ismertetett költséges és bonyolult technika alkalmazása helyett szemmel is jól meg lehet állapítani a láthatósági maximum helyét [10.3]. Végül problémát okozhat, ha a vizsgálandó mintának jelentős abszorpciója van. Ugyanis ez oly mértékben megváltoztathatja a detektált intenzitásfüggvény burkolóját, hogy amint ezt Naganuma és munkatársai kísérletileg igazolták [10.4], hamis csoportkésleltetés értékeket kapunk. Összefoglalva, a repülésiidő-interferometriával eddig elért legjobb időbeli felbontás tükrök esetén 12-szeres reflexiónál ±1/12 fs, más optikai elemekre ±1 fs, 10 nm-es spektrális bontásban a 400-750 nm-es hullámhossztartományon.
A repülésiidő-interferométerrel ellentétben ennél a módszernél szélessávú fényforrással világítjuk ki az interferométert. Ezért a kimeneten a fényforrás minden egyes spektrális komponensének interferenciája eredményeképp kialakult eredő intenzitást detektáljuk, ami lehetővé teszi, hogy a csoportkésleltetést már egy méréssel meghatározzuk a késleltetés függvényében mért intenzitásfüggvény Fourier-transzformáltjából [10.1,10.4,10.5]. A módszer matematikai hátterének megértéséhez lépjünk vissza a (10.7)-es egyenlethez. Látható, hogy a referenciakar tükrének folytonos késleltetésével kapott Ikorr(τ) keresztkorrelációs jel a referencia- és tárgykar spektrális fázisfüggvényét tartalmazó függvény Fourier-transzformáltja. Ez azt jelenti, hogy a diszperzív minta spektrális fázisfüggvényét valóban megkaphatjuk, ha a keresztkorrelációs jelnek vesszük a Fourier-transzformáltját. Innen kapta a módszer a nevét. Természetesen most is igaz, hogy először az üres interferométer két karja közötti maradék diszperziót is ki kell mérnünk, és csak ezután vizsgálhatjuk a diszperzív mintát.
A méréseknél két dologra kell ügyelni. Az egyik, hogy a karhosszkülönbség változását nagyon pontosan kell ismerni, mert a legkisebb torzulás is jelentős hibát okoz a fázis mérésében. Ezért rendszerint egy segéd He-Ne lézernyalábot is használunk. A másik probléma, hogy a fényforrás intenzitásának fluktuációja is zavarja a méréseket. Ezért vagy többször egymásután fel kell vennünk az intenzitás-késleltetés függvényt, vagy a Fourier-transzformáció után kapott fázisadatokon kell simítást végezni. Az előbbi a mérési időt növeli, az utóbbi viszont a spektrális feloldást rontja le. Tizenkét mérés időbeli átlagolásával Naganuma és munkatársai 6,5 fs-os időbeli felbontást értek el 0,46 THz-es (0,6 nm) spektrális bontás mellett [10.4] Az adatok további simításával az időbeli felbontást 0,65 fs-ra javították, de ekkor a spektrális bontás 4,6 THz-re (6 nm) csökkent le.
A spektrálisan bontott interferometria, vagy röviden spektrális interferometria kezdetei az 1900-as évek elejéig nyúlnak vissza. Ennek oka az elrendezés egyszerűségében rejlik. Ez a technika nem igényel mást, mint egy széles spektrumú fényforrással, pl. egy közönséges fehér lámpával kivilágított interferométert, melynek a kimenetét bontjuk egy spektrométerrel, spektrográffal vagy egy monokromátort használva. Az időtartománybeli mérési elrendezésekkel szemben e technika nagy előnye, hogy nem tartalmaz olyan alkatrészt, melynek mozgását nagy pontossággal kellene detektálni.
A vizsgált minta spektrális fázisfüggvénye a spektrális interferenciaképből különböző módszerekkel határozható meg. A spektrális interferometriát kezdetben üvegek és gázok törésmutatójának meghatározására, majd később fémtükrök spektrális fázistolásának mérésére használták. Az impulzusüzemű lézerek széleskörű elterjedésével az optikai elrendezésekben olyan eszközöket (pl. diszperzív lézertükröket, impulzuskompresszorokat, -nyújtókat, stb.) kezdtek használni, ahol a fémtükrökhöz hasonlóan a törésmutató helyett a spektrális fázisfüggvény ismerete vált fontossá. Ennek eredményeképpen a spektrálisan bontott interferometria számos változatát dolgozták ki.
A spektrálisan bontott interferometria két főcsoportra bontható az interferométert elhagyó referencia- és tárgynyaláb irányától függően. Egyik esetben a két nyaláb párhuzamos egymással, míg a másik esetben szöget zárnak be egymással (keresztezett nyalábú spektrális interferometria). Mindkét csoport további alcsoportra bontható annak megfelelően, hogy a spektrális fázisfüggvény térbeli változása is mérhető vagy nem. Ez részben függ a detektor típusától is. Míg a párhuzamos nyalábú változatban használhatunk diódasort illetve CCD chipet is, addig a keresztezett nyalábok esetében csakis kétdimenziós detektor (pl. CCD chip) jöhet szóba. A detektor kétdimenziós volta azonban még nem garantálja, hogy a spektrális fázisfüggvény térbeli változásáról is kapunk információt, ez a mérési módszertől is függ. A keresztezett nyalábú spektrális interferometriát szokták spektrálisan és térben bontott interferometriának is nevezni, azonban amióta a párhuzamos nyalábú változatnál is használnak kétdimenziós detektorokat, az elnevezés kissé megtévesztővé vált. Először tekintsük át a párhuzamos nyalábú spektrális interferometriai módszereket.
Amint említettük, ebben az esetben a referencia- és a tárgyimpulzus az interferométerből párhuzamosan lép ki egymáshoz képest időben késleltetve. Az interferométer kimenetén elhelyezett spektrométer a két impulzust spektrális komponenseire bontja, és a spektrométer detektorával e komponensek interferenciájának eredményét detektáljuk (10.4 ábra). A betét ábra egy olyan szimulált interferogramot mutat, melyet egy 15 fs-os, 800 nm központi hullámhosszú titán-zafír lézer impulzusával kapnánk, ha a diszperzív minta egy 10 mm vastag kvarc lemez lenne.

10.4. ábra. Spektrálisan bontott Mach-Zehnder interferométer egy tipikus spektrális interferogrammal
Ideális esetet feltételezve, a fénynyaláb és a detektor pixelei végtelenül vékonyak, a spektrométer felbontóképessége pedig végtelenül nagy. Ekkor a spektrométer kimeneténél elhelyezett detektor pixeleire már nem az impulzusok, hanem az őket alkotó monokromatikus hullámok esnek. Egyszerűség kedvéért tekintsük azt az esetet, amikor a monokromatikus komponensek síkhullámok. Így egy adott ω körfrekvenciának megfelelő pixelnél a térerősség a következőképpen adható meg:
 |
(10.9) |
A detektor pixelei azonban nem tudják lekövetni a térerősség időbeli változását, hanem felintegrálják a bejövő fényhullámokban lévő energiát. Ekkor a mért jel, azaz a spektrális intenzitás:
 |
(10.10) |
ahol I T (ω) és I R (ω) a tárgy- és a referenciakarból érkező fénynyaláb spektrális intenzitása (spektruma), valamint
 |
(10.11) |
a két kar közötti fáziskülönbség. Tekintve, hogy a valódi interferogramok esetében a fejezet elején ismertetett feltételek csak közelítőleg teljesülnek, így a (10.10) kifejezés is csak közelítőleg tudja megadni a valódi interferogramok spektrális intenzitását. Abban az esetben, ha nem túl nagy a két kar közötti késleltetés és jó a fényforrás térbeli koherenciája, a bemutatott összefüggések jól alkalmazhatók az interferenciamintázat leírására. Nagyobb késleltetések, illetve sűrű csíkrendszer esetén a láthatóság az említett hatások következtében leromlik.
A következőkben ismertetendő kiértékelési eljárásokhoz célszerű a mért interferogramból, illetve a tágy- és a referenciakar spektrális intenzitásból elő kell állítani a (10.10) összefüggést felhasználva az ún. normált interferogramot:
 |
(10.12) |
Először is megvizsgáljuk, hogy a kapott normált interferogramon milyen frekvenciáknál lesz az intenzitásfüggvénynek szélsőértéke. Ehhez a (10.12) egyenlet körfrekvencia szerinti első deriváltja zérus kell, hogy legyen:
 |
(10.13) |
Tekintsük elsőként azt az esetet, amikor a (10.13) egyenlet a dΦ/dω=0 következtében teljesül.
Annál a frekvenciaértéknél, amelyre ez teljesül, kialakul az ún. állandó fázisú pont [10.6]. Elnevezését az indokolja, hogy e pont környékén a spektrális fázis lassan változik (10.5. ábra).
10.5. ábra. Szimulált normált, spektrálisan bontott interferogram az állandó fázisú ponttal
Az állandó fázisú pont mozog az interferogramon a referenciakar késleltetésének változtatásával, ugyanis ekkor változik τ is, így más frekvenciaértéknél teljesül a dΦ/dω=0 feltétel:
 |
(10.14) |
A (10.14) összefüggésből látható, hogy az állandó fázisú pont helyét a két kar közötti τ késleltetés, a vizsgált diszperzív minta, valamint a két karban lévő optikai elemek csoportkésleltetés-függvénye határozza meg. Ebből következik, hogy különböző referencia- karhosszaknál vizsgálva az állandó fázisú pont helyét előbb az üres interferométerrel, majd a diszperzív mintával együtt, megmérhető a minta csoportkésleltetés függvénye.
Az állandó fázisú pont mozgásának irányából a csoportkésleltetés-diszperzió előjele egyértelműen meghatározható. Ha például azt látjuk az interferogramon, hogy az állandó fázisú pont a nagyobb frekvenciák felé mozdul a τ késleltetés értékének csökkentésével, az

10.6. ábra. Az állandó fázisú pont mozgása a késleltetés változtatásakor pozitív GDD-jű minta esetében
arra utal, hogy a rövidebb hullámhosszú komponensek az impulzus végén találhatók, azaz a csoportkésleltetés-diszperzió előjele pozitív. Emlékezzünk arra, hogy τ akkor pozitív, ha a tárgykar hosszabb a referenciakarnál. Ezért ha a késleltetés pozitív, az annyit jelent, hogy a tárgykarból érkező, pozitívan csörpölt impulzus késik a referenciaimpulzushoz képest, így a tárgyimpulzus eleje találkozik a referenciaimpulzussal. A tárgyimpulzus vivőfrekvenciája az impulzus elején alacsonyabb, és ekkor valóban az alacsonyabb frekvenciánál van az állandó fázisú pont. Amikor pedig negatív lesz a késleltetés, akkor a tárgyimpulzus megelőzi a referenciaimpulzust, így a referenciaimpulzus a tárgyimpulzus végével találkozik, ahol a tárgyimpulzus vivőfrekvenciája nagyobb. Ha a csoportkésleltetést ábrázoljuk a frekvencia függvényében, és erre polinomot illesztünk, akkor az illesztés együtthatói megadják a GDD, a TOD, FOD értékét.
Ha a minta diszperziója nem túl nagy, de kis felbontóképességű spektrométert használunk, vagy nagy a spektrométer felbontóképessége, de a minta diszperziója (pl. egy optikai szál vagy egy impulzuskompresszor esetében) is igen jelentős, akkor az interferogram egyes részein az interferenciacsíkok olyannyira besűrűsödnek, hogy a spektrográf kiátlagolja azokat (10.7. ábra).

10.7. ábra. Az állandó fázisú pont még akkor is jól felismerhető, amikor már a sűrű csíkrendszer elmosódik az interferogramon
Ilyen esetekben a diszperziónak az állandó fázisú pont módszerével történő meghatározása igen megbízható megoldás. A módszer hátránya azonban, hogy pontos méréshez sok interferogramon kell egyenként leolvasni az állandó fázisú pont helyét, ami meglehetősen időigényes, esetenként igen nehézkes. Kisebb diszperziók esetében az állandó fázisú pont kiszélesedik, ekkor az eljárás pontatlanná válik.
Bár a fejezet elején azt írtuk, hogy célszerű a mért interferogramból előbb a normált interferogramot elkészíteni, és csak azután kiértékelni, mégis sok esetben a mért interferogramon végzik el a kiértékelést. Ez nem okoz hibát akkor, ha a fényforrás spektrális intenzitása nem változik jelentősen az állandó fázisú pont környezetében.
Ha a (10.13) egyenlet teljesülésének másik feltételét vizsgáljuk, egy másik kiértékelési lehetőséghez jutunk. A sin(Φ(ω))=0 feltétel a minimum- és maximumhelyeket adja meg. Azon körfrekvenciáknál lesz maximum, ahol a fázis a 2π egész számú többszöröse, azaz Φ=2mπ esetén, és minimum ott lesz, ahol Φ=(2m+1)π (10.8. ábra).

10.8. ábra. Az interferencia minimumok és maximumok helyére vonatkozó feltételek
A kiértékelés során először is a felvett, majd normált interferogramról leolvassuk a maximumokhoz és minimumokhoz tartozó körfrekvencia értékeket. Ezekhez a fázist úgy rendeljük hozzá, hogy az adott maximum illetve minimum sorszámát (ez a fentebb említett m-nek felel meg) π-vel szorozzuk. Ha tehát az így meghatározott fázisértékeket a leolvasott körfrekvencia értékek függvényében ábrázoljuk, és egy ötöd rendű polinomot illesztünk a mért adatokra, akkor az illesztési paraméterekből adódnak a GDD, a TOD, FOD valamint a QOD értékei. Természetesen figyelembe kell venni, hogy az állandó fázisú pontnál a fázis menete előjelet vált, azaz az ezt követő pont is ugyanolyan fázisértékű lesz, mint az állandó fázisú pontot megelőző, valamint hogy ettől kezdve a fázisértékek nőnek a kapott görbe átfordul. Pontosan ez látszik a 10.9. ábrán, ahol a kék szaggatott vonal az illesztett görbe.

10.9. ábra. Spektrális interferogram minimum-maximum módszeres kiértékelésével kapott fázisfüggvény
E módszer volt a spektrális interferometria 1900 körüli születésétől kezdve a számítógépes kiértékelés elterjedéséig, azaz a 60-es évek végéig az egyetlen használható módszer, hiszen a fotolemezre felvett interferogram sötét csíkjait denzitométerrel pontosan le tudták olvasni. Később kissé feledésbe merült, ám nemrégiben sikerült ezt a módszert éppen optikai szálak diszperziójának méréséhez újra felfedezni [10.7]. Vegyük észre, hogy ennél a kiértékelési eljárásnál voltaképpen egyetlen interferogram felvétele is elegendő lenne a diszperzió pontos meghatározásához. A mérés pontossága növelhető sűrűbb csíkrendszer kialakításával, ha a referenciakar hosszának változtatásával növeljük a két kar közötti időbeli késleltetést. Minél szélesebb sávú fényforrást alkalmazunk, annál nagyobb tartományon tudjuk meghatározni a spektrális fázist, és így a diszperziós együtthatók mérési pontosságát növelni tudjuk. Ilyen esetekben azonban előtérbe kerül a módszer talán egyetlen hátránya, hogy nehézkes a minimumok, maximumok egyenkénti meghatározása, különösen, ha némi zajjal is terhelt a mérés. Megfelelő kiértékelő programmal a probléma megoldható.
Az állandó fázisú pont módszeréhez hasonlóan erre a módszerre is igaz, hogy gyakran a kiértékelést a mért interferogramon végzik el a normált interferogram helyett. Ez minimális hibát okoz a mérésben, ha nem változik jelentősen a spektrális intenzitás az interreferencia mintázat néhány periódusán belül.
Az előző fejezetekben ismertetett eljárásokkal szemben e módszer előnye a gyorsasága. A normált interferogramra egy fázismodulált ötöd rendű koszinusz-függvényt illesztünk a következő séma szerint:
 |
(10.15) |
A fenti képletben u betűvel jelöltük az illesztési paramétereket, melyeket, ha meghatároztunk, akkor ezek konstans szorosai adják a GDD, a TOD, FOD és a QOD értékeket. Az 10.10. ábrán pirossal a normált interferogramot, szaggatott kék vonallal pedig az illesztett görbét jelöltük.

10.10. ábra. Fázismodulált koszinusz-függvény illesztése a normált spektrális interferogramra
A módszer hátránya, hogy ha túl sűrűvé válik a csíkrendszer, akkor a spektrométer optikai elemei illetve a detektor pixeleinek véges mérete által meghatározott véges felbontóképesség miatt a csíkrendszer elkezd kiátlagolódni, ami a csíkrendszer láthatóságának csökkenéséhez vezet. Ebben az esetben az illesztőprogram által szolgáltatott eredmények kezdenek egyre pontatlanabbá válni, mivel a jel a vizsgált hullámhossztartomány mentén nem állandó amplitúdójú. Ilyenkor lassúsága ellenére az előbbi fejezetben ismertetett minimum-maximum módszer válik megbízhatóbbá.
Ebben a fejezetben az üvegek diszperziójának meghatározására már széles körben használt Fourier-transzformáción alapuló kiértékelési eljárást [10.8] ismertetjük, mely nem igényli a korábban ismertetett normálását az interefrogramnak. A módszer alapkövetelménye a sűrű interferencia csíkrendszer (10.11.a ábra), azaz viszonylag nagy, pikoszekundumos nagyságrendbe eső időbeli késleltetés. Először is a (10.10) egyenlet

10.11. ábra. (a) Szimulált spektrális interferogram és (b) Fourier-transzformáltja
interferenciát kifejező tagját az Euler-képletek alkalmazásával átírjuk, majd a felvett interferogramon végrehajtjuk a Fourier-transzformációt:
 |
(10.16) |
Ekkor az eredményül kapott I(t,τ') függvény négy tagja
 |
(10.17) |
voltaképpen három részre osztható (10.11.b ábra). A referencia- valamint a tárgykarból érkező impulzusok I T (ω) és I R (ω) spektrális intenzitása ω-ban lassan változó függvény. Így a megfelelő Fourier-transzformáltjaik I T (t) és I R (t) a t=0 körüli tartományban jelennek meg. Vegyük észre, hogy itt I T (t) és I R (t) nem a referencia- és tárgykarból érkező impulzusok intenzitásának időbeli függését jelöli, hanem az I T (ω) és I R (ω) spektrális fázisfüggvények Fourier-transzformáltját. Ezzel szemben a (10.16) összefüggés jobb oldali harmadik tagja, mely a mérendő fázisfüggvényt is tartalmazza, ω-ban gyorsan változó függvény. Így az Iint(t-τ')és az Iint(t+τ') Fourier-transzformáltjai a τ'=τ+dφ/dω illetve a -τ' időpontok környezetében találhatók. Az int jelölés arra utal, hogy a (10.16) egyenleben szereplő ún. interferenciás tagok Fourier-transzformáltjai. A τ' a tárgy- illetve a referenciakarból érkező két impulzus közötti időbeli késést jelöli. Ez két részből tevődik össze, egyrészt a két kar geometriai útkülönbségéből származó τ időkésésből, másrészt a dφ/dω tagból, azaz a diszperzív mintán valamint az interferométer optikai elemein fellépő időkésésből. Ez esetben a két t=0-ra szimmetrikus csúcs megjelenésének oka, hogy a Fourier-transzformáció valós függvényen történt.
A Fourier-transzformáltak közül a pozitív τ'-höz tartozót kivágjuk, majd visszatranszformáljuk a frekvenciatartományba. Ekkor a visszatranszformált függvény argumentumából kinyerhető fázis relatív körfrekvencia függvényből egy megfelelő polinom illesztésével megkaphatjuk a vizsgált mintára jellemző fázisderiváltak értékeit. Végül a spektrum és a fázisgörbe (10.12. ábra) (vagy a fázisderiváltakból számolt fázisfüggvény) felhasználásával egy újabb Fourier-transzformáció segítségével az impulzusalakot is meg tudjuk határozni.

10.12. ábra. A szimulált spektrum és a kapott fázisfüggvény
Meg kell jegyeznünk, hogy a spektrális fázisfüggvény és így az impulzusalak kis mértékben függ az említett időtartománybeli szűrésnél alkalmazott ablakszélességtől.
Eddigiekben, hogy a matematikai kifejezések egyszerűbbek legyenek, feltételeztük, hogy síkhullámok haladnak végig az interferométeren. Vegyük észre, hogy a fent ismertetett módszerek síkhullámoktól eltérő fényhullámok esetében is alkalmazhatók, csak ekkor a két kar közötti fáziskülönbséget megadó kifejezésben a térfüggést is bele kell venni. Így tehát a párhuzamos nyalábú spektrálisan bontott interferometria lehetővé teszi a diszperzív minta térfüggő fázisfüggvényének a meghatározását is.
Az interferometrikus technikák e csoportjánál az interferométert elhagyó referencia- és tárgynyaláb rendszerint a függőleges síkban szöget zár be egymással. Így erre a síkra merőlegesen jelennek meg interferenciacsíkok az interferométer kimenetén, melyeket egy spektrográffal bontunk fel oly módon, hogy a spektrográf rése függőleges állású (10.13. ábra).

10.13. ábra. Keresztezett nyalábú spektrálisan bontott Michelson interferométer diszperzív lézertükrök spektrális fázisának mérésére
A két kar közötti fáziskülönbség a párhuzamos nyalábú spektrális interferometriánál szereplő tagokon kívül egy speciális térfüggő taggal egészül ki [10.9]:
 |
(10.18) |
ahol γ<<1 rad az interferométer referenciatükrének dőlési szöge a vízszintes tengely körül, melynek az értéke akkor pozitív, ha előre dől a referencia tükör. A függőleges tengely legyen az y-tengely, és ekkor y0 jelöli azt a koordinátát, ahol a két kar között az időbeli késés τ (10.14. ábra).

10.14. ábra. A keresztezett nyalábú interferométer modellje τ=0 esetén. (a) Mindkét tükör diszperzió mentes. (b) A tárgykar tükre diszperzív
Ha a Michelson interferométer mindkét tükre diszperzió mentes, például arany tükör, akkor ahol a két tükörnek a nyalábosztó által alkotott képei metszik egymást, maximális intenzitást kapunk. A (10.18) egyenletből adódik, hogy egy-egy monokromatikus komponens esetében a kialakuló vízszintes interferencia-csíkrendszer intenzitáseloszlását egy koszinusz-függvény írja le, melynek a periódusa Λ=λ/2γ, azaz a hullámhosszal arányos (10.14.a ábra). Abban az esetben. ha a tárgykar tükrét kicseréljük egy diszperzív tükörre (pl. csörpölt tükörre), akkor a diszperzió mentes esethez képest az interferenciacsíkok eltolódnak a tükör spektrális fázisfüggvényével arányos módon. A (10.18) egyenletből adódik is egy kiértékelési módszer, koszinusz-függvényeket illesztünk a detektor pixel oszlopain detektált intenzitásértékekre, és a kezdőfázisokból megkapjuk a minta spektrális fázisfüggvényét. Vegyük észre, hogy ennél a módszernél is csak a GDD és annál magasabb rendű együtthatók határozhatók csak meg.
A 10.13 ábrán a fehér lámpa előtt egy vízszintes rést láthatunk. Erre azért van szükség, mert a fehér lámpa bár olcsó fényforrás, de a térbeli koherenciája nem túl jó. A rés szűkítésével ezen a helyzeten javíthatunk, mivel így csak az izzószál egy kicsiny részéből jutnak el fénysugarak az interferométerbe. A rés előtt lévő lencse párhuzamosítja a fénysugarakat, míg a polarizátor lineárisan poláros fényt állít elő. csörpölt tükrök esetében ügyelnünk kell arra, hogy a két polarizációs irányra eltérő a diszperzió értéke. Mivel sok esetben nem túl nagy a mérendő diszperzió, ezért több tükröt helyezünk el a tárgykarban oly módon, hogy kis szögben essen a tükrökre a fény. Ekkor polarizálatlan fénynél már a kapott interferenciamintázat olyan mértékben válik zajossá, hogy nem értékelhető ki.
Ezután vizsgáljuk meg, hogy mit láthatunk a spektrográf kimenetén, ha a Michelson interferométer mindkét tükre diszperziómentes, és a referenciakar tükrét előre-hátra tologatjuk (10.15 ábra).

10.15. ábra. Üres interferométer esetén a spektrálisan és térben bontott interferenciacsíkok alakja különböző τ késleltetéseknél [10.10]
Amikor τ=0 fs, akkor y0'-nél egy vízszintes csíkot látunk. Meglepő módon a csík nem világos, hanem sötét. Ennek oka az, hogy bár ennél a koordinátánál a két karnak a hossza egyenlő, azonban a nyalábosztó kockában lévő réteg egy π fázistolást okoz. Azt is láthatjuk, hogy a spektrálisan és térben bontott interferenciacsíkok széttartó egyenesek. Korábban már megállapítottuk, hogy a csíkok periódusa arányos a hullámhosszal, ezért nyilvánvaló, hogy így kell kinézni az interferenciaképnek. Vegyük észre, hogy ahogy növeljük a két kar közötti késleltetést, úgy válnak egyre meredekebbé az interferenciacsíkok, és a meredekségük előjele a késleltetés előjelétől függ. Így a csíkrendszer meredekségének méréséből meghatározható a két kar közötti késleltetés. Összefoglalva azt láthatjuk, hogy diszperzió mentes esetben az intereferenciacsíkok egyenesek.
Amint az kimutatható, az interferenciacsíkok alakja jól közelíti a diszperzív minta spektrális fázisfüggvényének alakját (10.16. ábra). Ez ennek a módszernek egyik nagy előnye, mivel a vizsgált minta diszperziójának gyorsan elvégezhető, kvalitatív ellenőrzését lehetővé teszi.

Abban az esetben, ha a diszperzió térfüggését is meg akarjuk határozni, akkor csak néhány periódusra illesztünk egy koszinusz-függvényt, és ezzel végig szkenneljük az interferenciaképet oszloponként [10.11].
Összefoglalva, ebben a fejezetben áttekintettük a fontosabb interferometrikus mérési módszereket, melyek alkalmasak az optikai elemek spektrális fázisfüggvényének mérésére. Az, hogy melyik módszert választjuk, részben függ az optikai elem spektrális fázisfüggvényének főbb jellemzőitől, a laborban rendelkezésre álló kísérleti eszközöktől, valamint az elvárt mérési pontosságtól.
Számítsa ki, hogy a spektrálisan bontott interferogramon 800 nm-es hullámhossznál mekkora az interferenciacsíkok közötti távolság, ha az interferométer két karjából érkező impulzusok között az időbeli késleltetés 1 ps?
Adjon egy közelítő formulát a minta másodrendű diszperziójának az egydimenziós spektrális interferogramból való meghatározására?
Ha a minta spektrális fázisfüggvényében csak a harmadrendű diszperziós tag szerepel, akkor hány állandó fázisú pont látható? Válaszát indokolja!
Állandó-e a kétdimenziós spektrálisan és térben bontott interferogramon a csíkok periódusa a hullámhossz függvényében, ha a mintának nincs diszperziója?
A spektrálisan és térben bontott interferogram melyik jellemző tulajdonsága függ az interferométer két karja közötti csoportkésleltetés különbségtől?
Hány fokban kell megdönteni a Michelson interferométer referenciatükrét, ha azt szeretnénk, hogy 800 nm-nél az interferenciacsíkok periódusa 50 µm legyen?
[10.1] A. Gosteva, M. Haiml, R. Paschotta, U. Keller: Noise-related resolution limit of dispersion measurement with white-light interferometers, J. Opt. Soc. Am. B22 (2005) 1868-1874..
[10.2] W. H. Knox, N. M. Pearson, K. D. Li, C. A. Hirlimann: Interferometric measurements of femtosecond group delay in optical components, Opt. Lett.13 (1988) 574
[10.3] Z. Bor, K. Osvay, B. Rácz, G. Szabó: Group refractive index measurement by Michelson interferometer, Opt. Commun. 78 (1990) 109.
[10.4] K. Naganuma, K. Mogi, H. Yamada: Group-delay measurement using the Fourier transform of an interferometric cross correlation generated by white light, Opt. Lett.15 (1990) 393.
[10.5] S. Diddams, J. C. Diels: Dispersion measurements with white-light interferometry, J. Opt. Soc. Am. B13 (1996) 1120..
[10.6] C. Sáinz, P. Jourdain, R. Escalona, J. Calatroni:Real time interferometric measurements of dispersion curves, Opt. Commun. 111 (1994) 632.
[10.7] J. Y. Lee and D. Y. Kim: Versatile chromatic dispersion measurement of a single mode fiber using spectral white light interferometry, Opt. Express14 (2006) 11608.
[10.8] L. Lepetit, G. Ch´eriaux, and M. Joffre: Linear techniques of phase measurement by femtosecond spectral interferometry for applications in spectroscopy, J. Opt. Soc. Am. B12 (1995) 2467.
[10.9] A.P. Kovács, R. Szipőcs, K. Osvay, Zs. Bor: Group delay measurement on laser mirrors by spectrally resolved white light interferometry, Opt. Lett.20 (1995) 788.
[10.10] A.P. Kovács, K. Varjú, K. Osvay, Zs. Bor: On the formation of white-light interference fringes, Am. J. Phys. 66 (1998) 985.
[10.11] A. Börzsönyi, A. P. Kovács, M. Görbe, K. Osvay: Advances and limitations of phase dispersion measurement by spectrally and spatially resolved interferometry, Opt. Commun. 281 (2008) 3051.
Tartalom
Amint a 6. fejezetben már szó volt róla, ha egy ultrarövid lézerimpulzus szögdiszperzióval bíró optikai elemen halad keresztül, akkor az impulzus frontja megdől a terjedési irányához képest, idő- és térbeli fázismoduláció (csörp) lép fel. Ezen hatások az impulzusok alkalmazási lehetőségeit erősen befolyásolják, ezért fontos, hogy rendelkezzünk olyan mérőberendezéssel, mellyel a kívánt pontossággal meg tudjuk mérni a szögdiszperzió nagyságát. Szintén volt már arról is szó, hogy a szögdiszperziónak két típusa létezik, az egyik a terjedésiirány-szögdiszperzió, míg a másik a fázisfront-szögdiszperzió. Ez a két mennyiség síkhullámok esetén ugyanakkora, míg Gauss-nyalábok esetében már általában eltérő értékű. Mivel e két mennyiség a fent említett jelenségeket eltérő módon befolyásolja, ezért szükséges, hogy mindkét típusú szögdiszperzió meghatározására mérési módszerekkel rendelkezzünk. A fejezet első részében a geometriai optikával is jól magyarázható terjedésiirány-szögdiszperzió, míg a második részben a hullámoptikai ismereteket is igénylő fázisfront-szögdiszperzió mérésére kifejlesztett módszereket tekintjük át.
A γ TI terjedésiirány-szögdiszperzió mérésénél azt vizsgáljuk, hogy az impulzust alkotó különböző hullámhosszú spektrális komponensek terjedési irányának szöge hogyan függ a hullámhossztól. E célra a legáltalánosabban használt módszer elvét a 11.1. ábra szemlélteti.

11.1. ábra. A terjedésiirány-szögdiszperzió mérésének elve.
Ha egy párhuzamosított fénynyalábot ejtünk egy f fókusztávolságú gyűjtőlencsére oly módon, hogy a nyaláb terjedési iránya a lencse optikai tengelyével θ szöget zár be, akkor a nyaláb a lencse fókuszsíkjában, de az optikai tengelytől Δ=fθ távolságban fókuszálódik le egy pontra. Itt feltételeztük, hogy θ kisebb 5 foknál, mely feltétel rendszerint teljesül a kísérleteknél. Az előbbiekből következik, hogyha egy rövid lézerimpulzust fókuszálunk le a lencsével, és az impulzus spektrális komponensei kissé eltérő irányban haladnak, akkor a lencse fókuszsíkját a spektrális komponensek különböző pontokban érik el. Ennek eredményeképpen egy kör alakú fényfolt helyett egy elnyúlt, elliptikus alakú foltot kapunk. Kvalitatív vizsgálatra már ez is alkalmas, hiszen a folt alakja alapján el tudjuk dönteni, hogy jelentősebb szögdiszerzió fellépett-e. Azonban előfordulhat, hogy olyan kicsi a szögdiszperzió értéke, hogy már nehezen ismerhető fel a fókuszfolt alakjából a szögdiszperzió jelenléte.
Sok esetben nem elég a kvalitatív vizsgálat, a szögdiszperzió pontos értékére is szükségünk van. Tekintettel arra, hogy a spektrális komponensek fókuszfoltjai átfednek, így ahhoz, hogy a terjedésiirány-szögdiszperziót meg tudjuk mérni, a különböző hullámhosszakhoz tartozó fókuszfoltokat egymástól valamilyen módon el kell különítenünk. E feladat egyik megoldása, hogy a lencse után elhelyezünk egy leképező spektrográfot oly módon, hogy a spektrográf optikai rése éppen a lencse fókuszsíkjában van, és a rés nyílása párhuzamos a szögdiszperzió síkjával. A 11.2. ábrán látható a kísérleti elrendezés, amikor az impulzusnak a vízszintes síkbeli terjedésiirány-szögdiszperzióját mérjük. A spektrográf kissé szokatlan helyzetben látható, mert a rése vízszintes, de a fentiekből következik, hogy ez kell ahhoz, hogy a vízszintes síkban fellépő szögdiszperziót mérni tudjuk. Bár a spektrográfok működését általában nem befolyásolja ha ilyen pozícióban használjuk, de sok esetben kényelmesebb lenne, ha nem kellene ilyen helyzetbe állítani. Ezen igény kielégítéséhez egy olyan nyalábforgató eszközt használhatunk, melyet a spektrográf előtt elhelyezve, a spektrográf billentése nélkül lehetővé teszi a vízszintes és a függőleges síkban is az impulzus szögdiszperziójának mérését.

11.2. ábra. Kísérleti elrendezés a vízszintes síkbeli terjedésiirány-szögdiszperzió mérésére.
A következőkben megvizsgáljuk, hogy hogyan lehet meghatározni a mért spektrum alakjából a spektrográf résének síkjában fellépő terjedésiirány-szögdiszperzió értékét. A spektrográf a rés képét állítja elő a kimenetén elhelyezett detektoron, jelen esetben egy CCD chipen. Ha nincs az impulzusban terjedésiirány-szögdiszperzió, azaz mindegyik spektrális komponens ugyanabba az irányba és egymáson haladva terjed, akkor a lencse fókuszsíkjában lévő résen ugyanabba a pontba fókuszálódnak (11.3.a ábra). A spektrográf spektrálisan felbontja a résen még egymáson lévő különböző hullámhosszakhoz tartozó fényfoltokat, így a spektrum a CCD chipen egy vízszintes sáv formájában jelenik meg ( 11.3.b ábra).

11.3. ábra. Ha a terjedésiirány-szögdiszperzió értéke zérus, akkor az impulzus spektruma vízszintes.
Abban az esetben, ha a terjedésiirány-szögdiszperzió értéke nem zérus, azaz az impulzus spektrális komponensei nem azonos irányba haladnak, akkor a különböző hullámhosszú komponensek a rés különböző részeire fókuszálódnak. Például a 11.4.a ábrán a hosszabb hullámhosszú, vörös színű komponens a rés felső, a kisebb hullámhosszú, sárga komponens a rés középső, míg a legkisebb hullámhosszú, kék komponens a rés alsó részére fókuszálódik. Spektrális bontás után ezért dőlt spektrumot kapunk ( 11.4.b ábra).

11.4. ábra. Ha a terjedésiirány-szögdiszperzió értéke nem zérus, akkor a spektrográf kimenetén dőlt spektrum látható.
Ha csak közelítőleg akarjuk a terjedésiirány-szögdiszperzió értékét tudni, akkor nagyon egyszerűen meg tudjuk határozni a spektrum meredekségéből. A spektrum meredeksége és az impulzus szögdiszperziója közötti kapcsolat egyszerű számolás után:
 |
(11.1) |
ahol N a leképező spektrográf nagyítása. A (11.1) egyenletből egyszerű átrendezéssel a szögdiszperzió kifejezhető. Vegyük észre, hogy a spektrum meredeksége nemcsak a szögdiszperzióval arányos, hanem a spektrográf nagyításával és a lencse fókusztávolságával is. Ennek alapján azt gondolhatnánk, hogy célszerű minél nagyobb nagyítású spektrográfot és minél nagyobb fókusztávolságú lencsét használnunk. Ami a nagyítást illeti, mivel ebben az esetben leképező spektrográfot használunk, ahol a spektrográf tervezésénél törekedni kell arra, hogy a leképezési hibák minél kisebbek legyenek, ezért a nagyítás rendszerint N=1 körüli érték, néha esetleg az N=2 eset is előfordul. Azaz a nagyítással nem tudjuk a mérőberendezésünk érzékenységét jelentős mértékben megnövelni. A lencse fókusztávolságát sem növelhetjük korlátlanul, ugyanis az f növelésével nő a fókuszfolt mérete is, így egyrészt fényt vesztünk, másrészt a spektrum y' tengely menti szélessége is elkezd nőni, ami a mérési pontosságot egy idő után már nem javítja. Az eddig alkalmazott eszközökben az f = 300-500 mm-es fókusztávolságú akromátlencse alkalmazása tűnt optimális megoldásnak.
Ha a terjedésiirány-szögdiszperzió pontos értékére van szükségünk, akkor a fent említett módszernél összetettebb adatfeldolgozást kell elvégeznünk. Ennek első lépése, hogy oszloponként (hullámhosszanként) veszünk egy-egy metszetet a mért spektrumból, és meghatározzuk a metszeteken a maximális intenzitáshoz tartozó y' értékeket pl. egy Gauss-függvény illesztésével. A spektrális komponensek terjedési irányának az optikai tengellyel bezárt szögét fejtsük Taylor-sorba másodrendig egy önkényesen választott λ0 referencia hullámhossz körül:
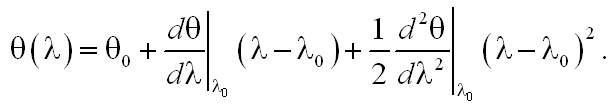 |
(11.2) |
A másodrendig történő sorfejtés a gyakorlatban előforduló esetekben egy megfelelő közelítés. Ekkor a spektrográf kilépési síkjában elhelyezett detektoron a λ hullámhosszú komponens y' koordinátája:
 |
(11.3) |
A (11.3) egyenletbe helyettesítve a (11.2) egyenletet, láthatjuk, hogy ha a hullámhosszkülönbség egy másodrendű polinomját illesztjük a függvényre, akkor a polinom együtthatóiból megkapjuk a lineáris és a másodrendű szögdiszperzió értékét is. Ezzel a módszerrel az eddig elért legnagyobb pontosság 0,2 μrad/nm volt, amikor is a vizsgált hullámhossztartomány a 100 nm-t meghaladta [11.1].
A módszernek egy komoly hátránya, hogy egyszerre csak egy síkban tudja a szögdiszperzió értékét mérni. Egy prizmás vagy egy rácsos impulzuskompresszor beállításánál előfordulhat, hogy a kompresszort elhagyó impulzus szögdiszperziójának síkja ferde. Ezt a problémát a fenti módszerrel eddigiekben úgy oldották meg, hogy egy vízszintes (11.5.a,b ábra) és egy függőleges (11.5.c,d ábra) síkbeli mérést végeztek oly módon, hogy vagy a spektrográfot, vagy a nyalábot forgatták el 90 fokkal. Azonban a mérés pontossága erősen függ a detektált spektrum szélességétől. Sajnos, amelyik irányra vonatkozóan a fókuszsíkban kialakuló spektrum vetülete kicsi (11.5.c ábra), a spektrográf kimentén detektált spektrum szélessége is nagyon kicsi lesz (11.5.d ábra), és így a mérési pontosság ebben az irányban eléggé leromlik. Ezt úgy lehetne elkerülni, ha folyamatosan forgatnánk körbe a nyalábot, és amikor legszélesebb a spektrum, akkor abban a síkban végezzük el a mérést. A felmerülő technikai problémák miatt ezzel a megoldással még nem találkozhatunk az irodalomban.

11.5. ábra. A ferde síkú szögdiszperzió mérésének problémája.
Az impulzuskompresszorok beállításánál általában nem annyira a nagy mérési pontosság a fontos, hanem inkább az, hogy lássuk, milyen síkban van még szögdiszperzió. E feladat megoldására egy olyan kísérleti elrendezést alkalmaztak, melynél a lézernyalábot ráfókuszálták egy kétdimenziós detektorra, egy CCD chipre úgy, hogy a nyaláb útjába helyeztek egymás után 4-5 kis sávszélességet átengedő színszűrőt [11.2]. Így a kamerán a 11.6. ábrának megfelelően jól láthatóvá vált a ferde síkú szögdiszperzió.

11.6. ábra. Tetszőleges síkban kialakuló szögdiszperzió mérése.
Nemrég kifejlesztésre került egy olyan eszköz, melynél nem kell cserélni a színszűrőket, hanem helyette egy Fabry-Perot interferométeren küldik keresztül a vizsgálandó lézerimpulzust [11.3]. Ebben az esetben a Fabry-Perot interferométer hullámhossz-szelektív transzmissziója biztosítja, hogy az impulzusnak csak bizonyos spektrális komponensei jutnak át rajta. Így sokkal egyszerűbben, és adott esetben sokkal jobb spektrális felbontásban megkapható a 11.6. ábrán látható, diszkrét pontokból álló spektrum, melyből a terjedésiirány-szögdiszperzió számolható.
Az előbbiekben láttuk, hogy a terjedésiirány-szögdiszperzió méréséhez relatíve egyszerű eszközök használata is elegendő volt, bár a legutóbbi, Fabry-Perot interferométeren alapuló elrendezésre már kevésbé mondható el. A γ FF fázisfront-szögdiszperzió mérésénél már nem tudjuk elkerülni az összetettebb, a környezeti hatásokra érzékenyebb interferometrikus elrendezések alkalmazását, mivel az impulzust alkotó spektrális komponensek fázisfrontjainak helyzetét csak ilyen típusú eszközökkel tudjuk meghatározni.
Korábban már volt arról szó, hogy ha az impulzus spektrális komponenseinek fázisfrontjai szöget zárnak be egymással, akkor ez az impulzusfront megdőléséhez vezet. Az impulzusfront dőlési szögének tangense a (6.7) egyenlet szerint arányos a γ FF fázisfront-szögdiszperzió értékével, azaz ha meg tudjuk mérni a front dőlési szögét, akkor abból már a (6.7) egyenlet alapján könnyedén meg tudjuk határozni a fázisfront-szögdiszperzió értékét is.
Az első mérési módszer, amit a fázisfront-szögdiszperzió mérésére kifejlesztettek, éppen az impulzusfront dőlési szögének meghatározásán alapul [11.4]. A méréshez szükséges kísérleti elrendezés sematikus ábrája a 11.7. ábrán látható.

11.7. ábra. A fázisfront-szögdiszperzió mérése az interferenciacsíkok láthatósági maximumának helye alapján.
A dőlt fronttal rendelkező ultrarövid lézerimpulzust egy tükrözött nyalábú Mach-Zehnder interferométerbe vezetjük be. Kihasználjuk azt, hogy ha az impulzus egy síktükörről verődik vissza, akkor a visszaverődés után a jobb és bal oldala felcserélődik. Ezért az interferométert úgy építjük meg, hogy az egyik karjában eggyel több síktükröt helyezünk el, és így az interferométer kimenetén az egyik karból érkező impulzus dőlési szöge éppen ellentétes a másik karból érkező impulzuséval. Az interferométernek szintén fontos eleme még az egyik karjában elhelyezett, állítható időbeli késleltetést okozó lineáris eltoló. Ily módon tudjuk változtatni a két karból érkező impulzusok közötti időkésést, ami azt eredményezi, hogy egyszer az impulzusok terjedési irány szerinti jobb oldalai fednek át időben (a. eset), majd a középső részük (b. eset), végül a bal oldaluk (c. eset). Ha úgy állítjuk be az interferométert, hogy az őt elhagyó két impulzus terjedési iránya kis szöget zárjon be egymással a függőleges síkban, akkor az interferométer után elhelyezett ernyőn vagy egy CCD chipen a nyaláb bizonyos részén vízszintes interferencia csíkokat láthatunk adott késleltetésnél. Változtatva a késleltetést, a csíkrendszer a nyaláb más-más részein lesz látható. Meghatározva az adott késleltetéseknél az interferenciacsíkok láthatósági maximumának helyét, meg tudjuk mérni az impulzusfront dőlési szögét, melyből a fázisfront-szögdiszperzió értékét már ki tudjuk számolni. Mivel a csíkok láthatósági maximumainak helyét nem lehet igazán nagy pontossággal megmérni, így ez a módszer nem alkalmas a fázisfront-szögdiszperzió értékének nagy pontosságú mérésére.
E probléma kiküszöbölésére a 11.7. ábrán látható elrendezést egy spektrográffal egészítették ki (11.8. ábra), ami abban különbözik az előbbi módszertől, hogy nem

11.8. ábra. A fázisfront-szögdiszperzió mérése tükrözött nyalábú, spektrálisan bontott Mach-Zehnder interferométerrel.
közvetlenül az interferométer kimenetét detektálják, hanem egy spektrográffal spektrálisan bontják [11.5]. A mérés elvének magyarázatához az egyszerűbb esetet vesszük, azaz amikor az impulzus spektrális komponensei síkhullámok. Először tételezzük fel, hogy nincs szögdiszperzió a nyalábban, azaz az impulzus spektrális komponenseinek fázisfrontjai egymással párhuzamosak. Mivel az interferométert úgy

11.9. ábra. a) A fázisfrontok helyzete, ha nincs fázisfront-szögdiszperzió. b) Az ennek megfelelő intenzitás az y-tengely mentén. c) A spektrálisan bontott interferenciacsíkok széttartó egyenesek.
állítottuk be, hogy a két karból érkező impulzus terjedési iránya között legyen egy θ0 szög, így az interferométer kimenetén az interferenciacsíkok periódusa λ/(2θ0). Mivel a csíkok periódusa arányos a hullámhosszal, így ha összeadjuk a különböző hullámhosszhoz tartozó koszinuszos intenzitáseloszlást, akkor valóban azt kapjuk, hogy a nyalábnak csak egy bizonyos részén láthatók a csíkok, a másik részén egymás hatását kompenzálva elmosódnak. Azonban ha spektrálisan felbontjuk a csíkrendszert, akkor megszüntetjük az átfedést, és a spektrálisan bontott csíkrendszer a teljes tartományon jó láthatóságú. Ebben az esetben a csíkok széttartó egyenesek.
Ha viszont fázisfront-szögdiszperzió van jelen a nyalábban, akkor a csíkok periodicitása nem arányos a hullámhosszal. A spektrálisan bontott

11.10. ábra. a) A fázisfrontok helyzete, ha van fázisfront-szögdiszperzió. b) Az ennek megfelelő intenzitás az y-tengely mentén. c) A spektrálisan bontott interferenciacsíkok görbültté válnak.
csíkrendszer csíkjai ekkor már nem egyenesek. A szögdiszperzió értékének pontos meghatározásához először a spektrálisan bontott csíkrendszerből meghatározzuk a csíkok periódusának hullámhosszfüggését, majd az így kapott θ*(λ) függvényre egy másodfokú polinomot illesztünk. Ezzel a módszerrel 0,2 μrad/nm pontosság érhető el.
Ebben a fejezetben láttuk, hogy a szögdiszperzió mérésére nem áll rendelkezésre olyan sok fajta mérési módszer, mint az optikai elemek spektrális fázisának mérésére. Azonban a kifejlesztett módszerekkel mind a terjedésiirány-, mind a fázisfront-szögdiszperzió a jelenlegi lézeres technológia által igényelt pontossággal mérhető.
Számítsa ki az impulzus terjedésiirány-szögdiszperziójának értékét, ha a pixelek függőleges mérete 5 µm, a detektor chipje 1280 x 1024 pixelből áll, a spektrográf a 700-900 nm-re eső spektrumot mutatja és a nagyítása 1:1, a spektrum dőlési szöge 30 fok és a lencse fókusztávolsága 50 cm?
Igazolja, hogy az egymással 2θ* szöget bezáró, λ hullámhosszú síkhullámok által létrehozott interferenciacsíkrendszer periódusa λ/2sin(θ*)!
Hogyan változik meg a spektrálisan bontott interferenciacsíkok alakja, ha fázisfront-szögdiszperzió lép fel?
A fázisfront-szögdiszperziót mérő elrendezésben miért szükséges az interferométer egyik karjában a fénynyaláb jobb és bal oldalát felcserélni?
Számítsa ki, hogy egy 60 fokos törési szögű kvarcprizmán való áthaladás után mekkora lesz a lézerimpulzusban a terjedésiirány-szögdiszperzió, ha a lézerimpulzus 56 fokban esik be, és az impulzus központi hullámhossza 800 nm?
Számítsa ki, hogy mekkora a két, 800 nm hullámhosszúságú síkhullám terjedési iránya által bezárt szög, ha az általuk létrehozott interferenciacsíkrendszer periódusa 30 µm?
[11.1] K. Osvay, A. P. Kovács, Zs. Heiner, G. Kurdi, J. Klebniczki, M. Csatári: Angular dispersion and temporal change of femtosecond pulses from misaligned pulse compressors, Sel. Top. IEEE Quantum.Electron. 10 (2004) 213.
[11.2] M Divoky, P Straka: Simple two-dimensional-imaging spectrograph with wedged narrow band filters, Rev. Sci. Instrum. 79 (2008) 123114
[11.3] A. Borzsonyi, Lucile Mangin-Thro, Gilles Cheriaux, K. Osvay: Real-time Two-dimensional Detection of Angular Dispersion of CPA Laser Beams,CLEO 2012 San Jose, USA 6-8 May 2012 CM1D.6
[11.4] G. Pretzler, A. Kasper, K.J. Witte: Angular chirp and tilted light pulses in CPA lasers, Appl. Phys. B70 (2000) 1
[11.5]K. Varjú, A. P. Kovács, G. Kurdi, K. Osvay: High-precision measurement of angular dispersion in a CPA laser, App Phys. B74 (2002) S259.
Tartalom
A 10. fejezetben ismertetett lineáris interferometrikus módszerek azon részével, melyekkel az optikai elem spektrális fázisfüggvénye mérhető, meg tudjuk határozni a lézerimpulzusok időbeli alakját az interferométer tárgykarjában elhelyezett optikai elem után abban az esetben, ha ismert az interferométer referenciakarjából érkező impulzus térerősségének időbeli lefutása. Sok esetben ilyen referencia impulzus nem áll rendelkezésre, például egy Ti:zafír lézeroszcillátorból kilépő impulzus időbeli alakjának mérésekor sem. E probléma megoldására fejlesztették ki az ún. önreferenciás mérési módszereket, ahol referencia impulzusként is a mérendő impulzus szolgál. Ezek a módszerek mind nemlineáris optikai jelenségen (pl. összegfrekvencia-keltésen, sum frequency generation, SFG) alapulnak. A (10.7) egyenletből következik, hogyha üres interferométert használunk, és a kimeneten egy lineáris detektort helyezünk el, akkor az interferométer referenciakarjának hosszát változtatva, a mért időben változó jel csak az impulzus spektrumáról hordoz információt, a fázisszerkezetéről nem. Ezzel szemben, amint az alábbiakban látni fogjuk, ha a mérendő impulzust két, időben teljesen azonos lefutású impulzusra osztjuk, és egy nemlineáris optikai elemen, pl. egy összegfrekvencia-keltő kristályon keresztül küldjük, akkor a referenciakar hosszának változtatásakor mért jel az impulzus fázisszerkezetéről is hordoz információt. A nemlineáris jelenségek hatásfoka az intenzitás négyzetével vagy magasabb hatványa szerint nő, azaz annál jobb a mérés jel-zaj viszonya, minél nagyobb a mérendő impulzus csúcsintenzitása. Ebből következőleg a lineáris módszerekhez képest nagyobb fényintenzitású jelekre van szükség. A lézerekből kilépő impulzusok vizsgálatánál ez nem okoz problémát. Ebben a fejezetben a négy legelterjedtebb önreferenciás módszert tekintjük át.
Először vizsgáljuk meg azt az esetet, amikor megelégszünk azzal, ha csak a vizsgált lézerimpulzus intenzitásának I(t) időbeli függését határozzuk meg, azaz az impulzus fázisszerkezetéről nem lesz információnk [12.1]. E célra a 12.1. ábrán látható kísérleti elrendezést használhatjuk. A mérendő impulzust kettéosztjuk, és a két impulzus között τ időbeli késleltetést hozunk létre. A két impulzust (E(t) és E(t-τ)) ráfókuszáljuk egy nemlineáris kristályra (pl. BBO, KDP), melyből nemcsak az eredeti vivőfrekvenciájú impulzusok lépnek ki a kristály túloldalán, hanem nemlineáris optikai folyamat eredményeképpen keltődik egy kétszeres vivőfrekvenciájú E sig (t,τ) impulzus is, ha időben átfed a két impulzus. A keltett impulzus intenzitásának nagysága arányos a két keltő impulzus időbeli átfedésével. A keltett impulzust ráfókuszáljuk egy lineáris detektorra.

12.1. ábra. Intenzitás-autokorrelátor sematikus rajza.
Megmutatható, hogy ekkor a detektor ID jele:
 |
(12.1) |
melyet intenzitás-autokorrelációs tagnak hívunk.

12.2. ábra. Egy 10 fs időbeli félértékszélességű, transzformlimitált lézerimpulzus intenzitás-autokorrelációs jele, amikor a két impulzus közötti időbeli késés a) -20 fs, c) 0 fs és e) 20 fs. A b), d), és f) ábrák az a), c) és e) esethez tartozóan a két karból érkező impulzus intenzitásának időbeli lefutását mutatják. A b), d) és f) ábrán a zöld szín a (12.1) integrálban szereplő szorzatfüggvény alakját szemlélteti.
Amikor a két impulzus időbeli átfedési kicsiny (12.2.b,f ábra) (lásd animáció), akkor a nemlináris optikai folyamat hatásfoka nagyon gyenge, így szinte nem keltődik összegfrekvenciájú jel, azaz a késleltetéstől függetlenül zérus vagy ahhoz közeli értékű az intenzitás-autokorrelációs jel (12.2.a,e ábra). Amikor pedig teljesen átfed a két impulzus (12.2.d ábra), akkor maximális nagyságú az összegfrekvenciájú jel, így a detektor jele is ekkor maximális (12.2.c ábra). Látható, hogy ez a módszer háttérmentes mérési módszer.
A kapott jel kiértékelése annyiban áll, hogy feltételezünk valamilyen, a valódi impulzus időbeli függését legjobban közelítő alakot, pl. Gauss-görbe alakot. Kimutatható, hogy ekkor az impulzus intenzitásfüggvényének időbeli félértékszélessége a korrelációs jel félértékei között mért időtartam 1,41-ed része. Ha ránézünk a 12.2.e ábrára, valóban azt látjuk, hogy a 10 fs-os impulzus esetében 14,1 fs a korrelációs jel félértékszélessége. A módszer hátránya, hogy nem ad semmilyen információt az impulzus fázisszerkezetéről. További hátrány, hogy a (12.1) matematikai alakból következően a detektor jele a késleltetésre szimmetrikus, azaz a kapott intenzitás-autokorrelációs jel alakja az impulzus esetleges időbeli aszimmetriájáról sem hordoz információt. Részletesebb vizsgálatokkal kimutatható, hogy különböző intenzitás-idő függvényeknek is ugyanaz az intenzitás-autokorrelációs jele, azaz az intenzitás-autokorrelációs jelből egyértelműen nem határozható meg a vizsgált impulzus időbeli alakja.
Mennél rövidebb impulzusokat vizsgálunk, annál kritikusabbá válik az elrendezésben alkalmazott optikai elemek impulzusnyújtó hatása. Ahogy a fentiekben láttuk, ha egy üveglemezen halad át az impulzus, akkor az üveg anyagi diszperziója miatt megnő az impulzus időbeli hossza. Mivel a növekedés mértéke jó közelítéssel arányos a lemez vastagságával, ezért minél vékonyabb lemezt kell alkalmazni. Az impulzusoknak a nemlineáris kristályra való fókuszáláshoz használt lencsének is van egy adott vastagsága, így az itt fellépő anyagi diszperzió csökkentésének minimalizálásához is minél vékonyabb lencsét kell használni. A 12.1. ábrán látható elrendezésben az egyik impulzus áthalad a nyalábosztó lemezen, a másik nem, így a két impulzus mire a kristályhoz ér, valójában nem lesz teljesen azonos időbeli alakú. Ez azt eredményezi, hogy az autokorrelációs jel aszimmetrikussá válik. A nemlineáris kristály esetében egyrészt a kristály anyagi diszperziója jelent problémát. Másrészt a frekvenciakétszerezés sávszélessége a kristály vastagságának csökkentésével növekszik, így minél rövidebb impulzust vizsgálunk, annál vékonyabb kristályra van szükségünk. Körülbelül 20 fs időtartamú impulzusokat lehet még vizsgálni ezzel a módszerrel, és ekkor a kristály vastagsága már csak kb. 10 µm lehet.
Összefoglalva, azt láttuk, hogy az intenzitás-autokorrelációval csak az impulzus időtartamáról kapunk információt, a spektrális fázisáról nem. Mivel a lézerimpulzusok számos alkalmazásánál ez utóbbi mennyiség ismerete is fontos, ezért továbbfejlesztették a fent ismertetett elrendezést, melynek részleteit a következő fejezetben tekintjük át.
Az interferometrikus autokorrelációs kísérleti elrendezés szintén egy interferométeren, egy Michelson interferométeren alapul (12.3. ábra) [12.1]. A mérendő impulzust az interferométerbe lépve kettéosztjuk egy nyalábosztó lemez segítségével. Az interferométer egyik karjának hosszát változtatva az interferométerből kilépő két impulzus közötti időbeli késés is változik. Mivel az ábrán a változtatható hosszúságú karban haladó impulzus a nyalábosztó üveglemezen kettővel többször halad át, ezért a másik karba egy pontosan ilyen vastagságú lemezt kell betenni. A mérés detektálási részét illetően két megoldás terjedt el. Az egyik esetben az interferométerből kilépő impulzusokat egy nemlineáris kristályra fókuszáljuk, és a keletkezett frekvenciakétszerezett (felharmonikus) jelet lineáris fotodiódával detektáljuk oly módon, hogy a felharmonikus jelről egy színszűrővel leválasztjuk az alapharmonikus jelet (12.3.a ábra). A másik megoldás, amikor egyszerűen egy olyan nemlineáris fotodiódát használunk (12.3.b ábra), amelyik a mérendő impulzus frekvenciaspektrumában nem abszorbeál, csak a kétszeres frekvenciákon.

12.3. ábra. Interferometrikus autokorrelátor a) nemlineáris optikai kristállyal és lineáris fotodetektorral, vagy b) kristály nélkül, csak nemlineáris fotodiódát használva.
A detektált interferometrikus autokorrelációs (IAC) jel:
 |
(12.2) |
A 12.4.a ábrán látható egy 800 nm központi hullámhosszú, 10 fs-os időbeli félértékszélességű transzformlimitált impulzus esetében kapható interferometrikus autokorrelációs jel, melyet a (12.2) összefüggés alapján számoltunk ki. A 12.4.b ábra alsó grafikonján az autokorrelációs jel utolsó pontjához tartozóan látható a két impulzus egymáshoz képesti időbeli helyzete. Ez éppen a két impulzus közötti azon késleltetés, amikor az egyik impulzus térerősség maximuma a másik impulzus térerősség maximumával egybeesik. Azonban már időben nem fednek át teljesen, ezért bár erősítő interferencia van közöttük, de a detektor jelének intenzitása már nem lesz olyan nagy, mint amikor teljes átfedésben voltak (τ=0 időbeli késleltetéskor).

12.4. ábra. a) Egy 10 fs-os időbeli félértékszélességű, 800 nm központi hullámhosszú transzformlimitált impulzus interferometrikus autokorrelációs jele egy adott késleltetésig (animáció). b) Az a) ábrán látható autokorrelációs jel utolsó pontja esetén az interferométer két karjából érkező impulzusok térerősségének időbeli lefutása.
Megmutatható, hogy az IAC jel értékeinek aránya abban a két esetben, amikor a két impulzus között nincs késés, illetve amikor már nem fednek át időben 1:8. (12.2)-ből következik, hogy az intenzitás-autokorrelációhoz hasonlóan a τ késleltetésre szimmetrikus a detektor jele. Ez azt eredményezi, hogy ennél a módszernél is, ha netán a lézerimpulzusnak aszimmetrikus is lenne az időbeli alakja, az IAC jel akkor is szimmetrikus lesz.
A detektált jelből az impulzus időbeli alakjának meghatározása nem igazán egyszerű még számítógépes kiértékelő programot használva sem, ezért manapság ezt a technikát inkább csak kvalitatív impulzusdiagnosztikára használják. A 12.5. ábrán láthatjuk, hogy a transzformlimitált impulzushoz képest (12.5.a ábra) az 1 cm vastag kvarc üveghasábon való áthaladás után (12.5.b ábra) az autokorrelációs jel időben jelentősen kiszélesedik, és egy válla is lesz. Azaz valóban, ha egy oszcilloszkópon nézzük a jelet, akkor jól látható már egy 1 cm vastag üveglemeznek is az impulzus időbeli alakjára gyakorolt hatása.

12.5. ábra. Másodrendű interferometrikus autokorrelációs jele a) egy 10 fs-os transzformlimitált impulzusnak, illetve b) 1 cm vastag kvarc hasábon való áthaladás után.
A hosszadalmas kiértékelési procedúra helyett általában arra használjuk az IAC jelet, hogy azt ellenőrizzük, hogy a vizsgált impulzus mennyire közel van egy transzformlimitált impulzushoz. Ehhez leolvassuk a jel időbeli félértékszélességét, mely a 12.5.a ábrán 16 fs. Feltesszük, hogy az impulzus spektruma például Gauss-görbe alakú. Ekkor az elméletből adódik, hogy az IAC jel időbeli félértékszélességét 1,6-tal osztva kapjuk meg az impulzus intenzitásának időbeli félértékszélességét. Ezt megszorozva a spektrométerrel felvett spektrum körfrekvenciában mért félértékszélességével, ha a szorzat értéke közel van a 0,44-hez, akkor ez azt jelenti, hogy az impulzusunk jó közelítéssel transzformlimitált.

12.6. ábra. Az impulzusok időbeli alakja a) 10 fs-os transzformlimitált impulzus, b) GDD=200 fs2 és c) TOD=2000fs3 esetében, valamint d-f) a megfelelő interferometrikus autokorrelációs görbék.
Bár a 12.6. ábrasor azt mutatja, hogy az interferometrikus autokorreláció egy hasznos módszer az ultrarövid impulzusok fázisszerkezetének vizsgálatánál, de kvantitatív vizsgálathoz nem túl gyors, és a kapott spektrális fázisfüggvény nem is pontos minden esetben.
A FROG szó a Frequency Resolved Optical Gating elnevezésből ered, mely arra utal, hogy ebben az esetben egy kapu (gate) impulzusra lesz szükségünk a mérendő impulzus vizsgálatához [12.2,12.3]. A FROG technikának több változata is van aszerint, hogy milyen nemlineáris folyamat során állítjuk elő a kapuimpulzust. Így van másodharmonikus keltésen (second harmonic generation, SHG), polarizáción (polarization gating, PG), öndiffrakción illetve harmadik harmonikus keltésen alapuló FROG. Ezek közül két leggyakrabban használt változattal, az SHG-FROG-gal illetve a PG-FROG-gal foglalkozunk, melyek segítségével a FROG technika lényege megérthető, illetve megmutatjuk a különböző technikák mennyire különböző spektrogramokhoz vezethetnek.
Először tekintsük a legérzékenyebb FROG technikát, az SHG-FROG-ot, melynek a mérési elrendezése (12.7. ábra) nagyon hasonlít a 12.1. ábrán látható intenzitás-autokorrelátorhoz. A különbség csak annyi, hogy az elrendezésben használt detektor nem egy fotodióda, hanem egy spektrométer.

12.7. ábra. Az SHG-FROG kísérleti elrendezés sematikus rajza.
A keletkezett E sig felharmonikus jel spektrumát a két impulzus közötti időbeli késleltetés függvényében detektáljuk, azaz a kapott spektrogram:
 |
(12.3) |
ahol
 |
(12.4) |
A (12.3) kifejezést felírhatjuk egy másik formában is, ami talán jobban rávilágít a FROG technika lényegére:
 |
(12.5) |
ahol Ę(t) és ĝ(t-τ) jelöli a mérendő és a kapuimpulzust. A fenti három egyenlet összevetéséből azt látjuk, hogy az SHG-FROG esetében a kapuimpulzus egyszerűen a mérendő impulzus önmaga. A (12.5) egyenletből adódik, hogy a kapott spektrogram két mennyiségtől függ, a mérendő és a kapuimpulzus közötti késleltetéstől, illetve a körfrekvenciától.
Ezután vizsgáljuk meg, hogy hogyan néz ki az SHG-FROG spektrogramja egy 10 fs időbeli hosszú, 800 nm központi hullámhosszú transzformlimitált impulzusnak, valamint ha a spektrális fázisfüggvénye oly módon változik meg, hogy a nemlineáris része vagy csak GDD-t, vagy csak TOD-t, vagy csak FOD-t tartalmaz.

12.8. ábra. Számolt SHG-FROG spektrogramok (alsó sor) a megfelelő impulzusalakokkal (felső sor), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak GDD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja.
A 12.8. ábra azt az esetet mutatja, amikor a GDD értéke -1000 fs2, 0 fs2 és 1000 fs2. Az ábra felső sora az említett GDD értékeknél létrejövő impulzusalakot, azaz az impulzus intenzitásának időbeli függését mutatja. Ha összevetjük a spektrogramokat az impulzus időbeli alakjával, akkor megállapíthatjuk, hogy a spektrogramok központi frekvenciájánál (4,7 fs-1) az időbeli hossz körülbelül olyan nagyságú, mint az impulzus időbeli hossza. Vegyük észre, hogy a spektrogram központi körfrekvenciája kétszerese az impulzus 800 nm-es központi hullámhosszának megfelelő 2,35 fs-1 értékű körfrekvenciájának, összhangban azzal, hogy a detektált jel frekvenciakétszerező kristályban keletkezik. Megállapíthatjuk, hogy a spektrogram vizuális megfigyelésével az impulzus időbeli hosszát meg tudjuk becsülni. Azonban a spektrogram alakja nem függ a GDD előjelétől, hasonlóan az intenzitás-autokorrelációval kapott jelekhez. Továbbá a GDD által okozott csörpről, azaz hogy az impulzus vivőfrekvenciája változik az időben, sem kapunk információt, hiszen minden késleltetésértéknél a spektrum közepe ugyanazon körfrekvenciánál van.

12.9. ábra. Számolt SHG-FROG spektrogramok (alsó sor) a megfelelő impulzusalakokkal (felső sor), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak TOD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja.
A 12.9. ábra azt mutatja, hogy a központi frekvenciánál a spektrogram időbeli hossza hasonló nagyságú a TOD hatására létrejött impulzussorozat első tagjának időbeli hosszához, azonban nem látható semmilyen alakzat, ami az impulzussorozatra utalna. Ebben az esetben sincs különbség a pozitív illetve a negatív TOD-nál a spektrogram alakjában.

12.10. ábra. Számolt SHG-FROG spektrogramok (alsó sor) a megfelelő impulzusalakokkal (felső sor), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak FOD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja.
A 12.10. ábra a FOD hatását mutatja. Itt is azt láthatjuk, amit már a GDD-nél és a TOD-nál is megállapítottunk, hogy a spektrogram időbeli hossza hasonló az impulzuséhoz, és az ellenkező előjel nem gyakorol hatást a spektrogram alakjára.
Ezután tekintsünk egy másik elrendezést (12.11. ábra), a polarizációkapuzott FROG-ot. Ebben az esetben is a mérendő impulzust kettéosztjuk, időben késleltetjük őket egymáshoz képest, és ráfókuszáljuk egy nemlineáris közegre, jelen estben például egy kvarclapra. A két impulzus közül azt nevezzük próbaimpulzusnak, amelyik az ábrán alul halad, és a nemlineáris közeg előtt átmegy egy polarizációs osztókockán. A kocka úgy van beállítva, hogy például a vízszintes polarizációjú fényt engedi át, ez felel meg a 0 foknak. A próbaimpulzus a közeg után ismét egy polarizációs osztókockához ér, amelyik viszont a függőleges polarizációjú fényt engedi át. Ebből következőleg, ha a kvarclapot nem éri a másik impulzus, akkor a második kockán már nem megy tovább fény, a spektrométer nem detektál jelet.

12.11. ábra. A polarizációval kapuzott PG-FROG technika mérési elrendezése.
A kapuimpulzus útjába egy félhullám lemezt teszünk, és a lemez segítségével elforgatjuk az impulzus polarizációs síkját oly módon, hogy az a vízszintes síkkal 45 fokot zárjon be. Amikor eléri a kvarclemezt, ha kellően nagy az intenzitása, akkor abban a Kerr-effektus révén kettőstörést hoz létre. Ha ekkor halad át a kvarclapon a próbaimpulzus is, akkor kissé elfordul a polarizációs síkja, és így a második polarizációs osztókockán a fényének egy része átjut, elérve a spektrométert. Ebben az esetben a keltett jel térerőssége:
 |
(12.6) |
Fontos megjegyezni, hogy nem szükséges, hogy a próba- és a kapuimpulzus a mérendő impulzus két másolata legyen. Vannak olyan megoldások is, amikor a kapuimpulzust egy másik lézer szolgáltatja.
Vizsgáljuk meg a PG-FROG technikával kapható spektrogramokat. Most is egy 10 fs-os, 800 nm központi hullámhosszú impulzusra végezzük el a szimulációt.

12.12. ábra. Számolt PG-FROG spektrogramok a csoportkésleltetés görbével (piros vonal), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak GDD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja és csoportkésleltetés görbéje.
A 12.12. ábra azt az esetet mutatja, amikor a GDD értéke nem zérus. Egyből szembetűnik, hogy az SHG-FROG-gal ellentétben a GDD előjelére is következtethetünk a spektrogram alakjából. Az is látható, hogy jó közelítéssel megegyezik a spektrogram középvonala a csoportkésleltetés-görbével, azaz a csörpöltség mértékét is vizuális megfigyeléssel meg tudjuk becsülni.

12.13. ábra. Számolt PG-FROG spektrogramok a csoportkésleltetés görbével (piros vonal), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak TOD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja és csoportkésleltetés görbéje.
A 12.13. ábra a TOD-ra vonatkozóan mutatja a spektrogramokat. Itt is érvényesek a 12.12. ábra kapcsán tett észrevételek.

12.14. ábra. Számolt PG-FROG spektrogramok a csoportkésleltetés görbével (piros vonal), ha az impulzus spektrális fázisfüggvényének nemlineáris része csak FOD-t tartalmaz, illetve összehasonlításképpen középen a transzformlimitált impulzus (10 fs@800 nm) spektrogramja és csoportkésleltetés görbéje.
A FOD esetében is (12.14. ábra) a spektrogram középvonala szépen követi a csoportkésleltetés görbe menetét.
Összefoglalva elmondhatjuk, hogy a PG-FROG-gal kapható spektrogramok sokkal informatívabbak az SHG-FROG-gal kapottaknál, ha pusztán csak vizuális megfigyelést végzünk. Kérdés, hogy a spektrogramok kvalitatív vizsgálatán túl milyen módon lehet kvantitatív eredményekre jutni. Emlékezzünk arra, hogy az interferometrikus autokorrelációs görbéből csak az impulzus időbeli hosszát lehet meghatározni, míg az interferometrikus autokorreláció esetében iteratív módon, általában megkaphatjuk a spektrális fázist, de elég nagy a kiértékelés bizonytalansága, és a függvény előjele nem határozható meg.
A FROG technikákkal kapott spektrogramokat is csak iteratív módon lehet kiértékelni. Mindegyik technika esetében a 12.15. ábrán látható eljárást alkalmazzuk. A kiértékelés első

12.15. ábra. A FROG spektrogramok iteratív kiértékelésének menete.
lépéseként feltételezünk egy Ę(t) térerősségfüggvényét az impulzusnak. Ebből ki tudjuk számolni az ehhez tartozó Ę sig (t,τ) korrelációs jelet, mely az adott technikától függ. Ezután elvégezzük rajta a Fourier-transzformációt. A kapott Ę sig (ω,τ) függvény abszolútérték-négyzetét véve egy spektrogramot kapunk. Ezt összevetjük a mért I(ω,τ) spektrogrammal. Ha jelentős az eltérés, akkor a mért spektrogram alapján korrigáljuk a korábban kiszámolt Ę sig (ω,τ) függvényt, majd elvégezzük rajta az inverz Fourier-transzformációt. A kapott Ę' sig (t,τ) függvényből számolunk egy újabb Ę(t) térerősségfüggvényt. Addig folytatjuk az iterációt, ameddig a számolt spektrogram a mérttel egy bizonyos hibahatáron belül meg nem egyezik. Az iteráció utolsó lépésénél használt Ę(t) térerősséget tekintjük a mérendő impulzus térerősségfüggvényének.
A SPIDER (Spectral Phase Interferometry for Direct Electric Field Reconstruction) technikát Iaconis és Walmsley dolgozta ki [12.4,12.5,12.6]. Bár ez a technika is nemlineáris optikai folyamatot használ, azonban a FROG-tól eltérően a 10. fejezetben tárgyalt spektrális interferometriával mutat rokonságot. A kísérleti elrendezés sematikus rajzát mutatja a 12.16 ábra.
12.16. ábra. A SPIDER technika egyik megvalósítási lehetősége.
A mérendő impulzust két részre osztjuk egy nyalábosztó segítségével. Az egyik impulzust időben jól megnyújtjuk például egy rácspár alkalmazásával, míg a másik impulzust újból kettéosztjuk egy Mach-Zehnder interferométerben, és egy τ időbeli késést állítunk be közöttük. Egy összegfrekvenciakeltő (SFG) kristályon találkozik össze a két, egymáshoz képest τ idővel késleltetett impulzus az időben kinyújtott impulzussal. Az időbeli nyújtás azt is eredményezi, hogy az impulzus csörpölődik, azaz a vivőfrekvenciája időben változik. Ha rácspárral nyújtjuk ki az impulzust, akkor az impulzus elején a vivőfrekvencia nagyobb, a végén viszont kisebb. Mivel a Mach-Zehnder interferométerből jövő két, azonos időbeli lefutású, csak egymáshoz képest időben késleltetett impulzus a csörpölt impulzus Ω1 és Ω2 vivőfrekvenciájú részével találkozik, így az összegfrekvencia-keltés két kissé különböző vivőfrekvenciájú impulzust eredményez. Az SFG kristályban keletkezett két impulzus vivőfrekvenciája közötti különbség: Ω= Ω2-Ω1. A két spektrálisan eltolt impulzus interferál egymással, és az interferogramot spektrálisan bontjuk.
A kapott spektrális interferogram intenzitáseloszlása:
 |
(12.7) |
ahol a két impulzus közötti fáziskülönbség:
 |
(12.8) |
Az interferogram átlagos modulációs periódusát a τ késleltetés határozza meg. Az interferogramból a 10. fejezetben ismertetett Fourier-transzformációs kiértékelési módszerrel kaphatjuk meg első lépésként a ΔΦ fáziskülönbséget. A mérés előtt fel kell venni csak a Mach-Zehnder interferométerből jövő két impulzussal előálló spektrálisan bontott interferogramot, melyből szintén a Fourier-transzformációs módszerrel meghatározzuk az ωτ fázistagot. Ezt meg tudjuk könnyedén tenni, mert a nemlineáris kristályban, ami gyakran 30-100 µm vastag BBO-kristály szokott lenni, az I. típusú összegfrekvencia-keltés mellett a frekvenciakétszerezés folyamata is lejátszódik (12.17. ábra), azaz a kristályba belépő impulzusok hatására a kristály túloldalán kilép a kétszeres frekvenciájú impulzus is. Így az egymást τ idővel követő infravörös impulzusok hatására a kristályból kilép két kék színű ultrarövid lézerimpulzus szintén τ követési idővel. E két impulzus egy modulált spektrumot fog létrehozni, melynél a moduláció periódusának reciprokából adódik τ értéke.

12.17. ábra. A BBO kristályban nemcsak összegfrekvenciakeltés (SFG), hanem frekvenciakétszerezés (SHG) is történik.
Az ωτ tagot kivonva a mért fáziskülönbségből, az impulzus spektrális fázisa az alábbi módon határozható meg. Jelöljük a fáziskülönbséget δΦ(ω)-val, azaz
 |
(12.9) |
Tételezzük fel, hogy a Φ(ω) spektrális fázis az ω0 körfrekvenciánál zérus:
 |
(12.10) |
és ekkor (12.9) és (12.10) alapján
 |
(12.11) |
Tehát így megkaptuk a spektrális fázis értékét az ω0-Ω körfrekvenciánál. Ebből az értékből viszont megkaphatjuk az ω0-2Ω körfrekvenciánál is az értéket a fentiekhez hasonló módon:
 |
(12.12) |
A fenti eljárást ismételve a vizsgált tartományban Ω körfrekvenciánként meg tudjuk határozni az impulzus spektrális fázisát. Ha az Ω körfrekvencia-tartományon a spektrális fázis nem változik túl nagyot, akkor jó közelítéssel érvényes, hogy
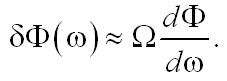 |
(12.13) |
Ebből következően a spektrális fázis egy integrálással adódik:
 |
(12.14) |
Ez utóbbi eljárás előnye, hogy itt minden mért értéket felhasználunk, míg a fentebbi módszernél csak Ω értékenként szereplő adatokat.
A mérés utolsó lépése, amikor az impulzus spektrumát is felvéve, egyszerűen egy újabb Fourier-transzformáció alkalmazásával megkapjuk az impulzus időbeli alakját. Az elrendezésben alkalmazott időbeli nyújtásnak olyan nagynak kell lenni, hogy a Mach-Zehnder interferométerből érkező impulzusok találkozva a csörpölt impulzussal, azt kvázimonokromatikus fényhullámnak érezzék.
Ahhoz, hogy képet alkossunk arról, hogy a fenti paraméterek milyen nagyságrendbe esnek, egy megépített SPIDER paraméterei [12.7]: a rácsok karcolata 1200 vonal/mm, a beesési szög 37°, a rácsok közötti távolság 10 cm. Egy ilyen paraméterű rácspárnál egy 100 fs-os impulzus kb. 20 ps-ra nyúlik meg. A Mach-Zehnder interferométer a két impulzus között τ ≈ 2 ps késleltetést hoz létre. Ekkor az impulzus körfrekvenciája 374 THz-zel tolódik el, míg a két impulzus közötti körfrekvencia-elcsúszás Ω= 1,7 THz. A SPIDER elrendezés megtervezésnél figyelni kel arra, hogy a nyalábosztó üveglemezeknek van diszperziójuk, ami torzítja a mérést, ha a két impulzus közül az egyik kevesebb utat tesz meg benne.
A SPIDER technika előnye a FROG-gal szemben, hogy az interferogram kiértékelése nem igényel időben hosszadalmas iterációs eljárást. Ezzel a módszerrel 10 ps vagy annál rövidebb impulzusok időbeli alakja határozható meg. Az alsó korlátot főként az szabja meg, hogy az SFG kristályban a fázisillesztési feltételnek egyre nagyobb hullámhossztartományon kell teljesülni. Ez oly módon teljesíthető, hogy egyre vékonyabb és vékonyabb kristályokat használunk. A néhány optikai ciklusból álló lézerimpulzusok időbeli alakját sikerült már ezzel a módszerrel is megmérni, ekkor a kristály vastagsága már csak 30 µm volt.
Mi a különbség az interferometrikus és az intenzitás-autokorrelációs jel létrejötte között?
Hogyan lehet egy interferometrikus autokorrelátorból másodharmonikus-keltésen alapuló FROG berendezést készíteni?
Írjon programot, mely kiszámolja egy 10 fs-os transzformlimitált impulzus interferometrikus autokorrelációs görbéjét!
Mi a különbség és mi a hasonlóság a másodharmonikus-keltésen alapuló illetve a polarizációkapuzott FROG berendezés között?
Melyik impulzusmérési módszer(ek) használ(nak) iteratív kiértékelési eljárást?
Melyek a főbb lépései a SPIDER technikával kapott interferogram kiértékelésének?
[12.1] J.-C. M. Diels, J. J. Fontaine, I. C. McMichael, F. Simoni: Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy, Appl. Opt.24 (1985) 1270
[12.2] R. Trebino and D. J. Kane: Using phase retrieval to measure the intensity and phase of ultrashort pulses: frequency-resolved optical gating. J. Opt. Soc. Am. A.10 (1993) 1101
[12.3] D. J. Kane and R. Trebino: Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse using frequency-resolved gating. Opt. Lett.18 (1993) 823.
[12.4] C. Iaconis and I. A. Walmsley: Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses, Opt. Lett.23 (1998) 792
[12.5] C. Iaconis and I. A. Walmsley: Self-referencing spectral interferometry for measuring ultrashort optical pulses, IEEE J. Quantum Electron. 35 (1999) 501.
[12.6] M.E. Anderson, A. Monmayrant, S.-P. Gorza, P. Wasylczyk, and I.A. Walmsley:SPIDER: A decade of measuring ultrashort pulses, Laser Phys. Lett. (2008) 1
[12.7] J. B. Macpershon: Characterisation and optimization of ultrashort laser pulses, MSc thesis (2003)


