Csillagászati laboratórium I.
8. Pulzárok rádiócsillagászati vizsgálatai

Célkitűzések

A rádiótávcsövek használatának elvi elsajátítása, egy többcsatornás vevő jeleinek rögzítése, a jelek optimális megjelenítése, majd a vizsgált pulzárok legfontosabb jellemzőinek megbecslése (periódus, hullámhosszfüggő diszperzió meghatározása, ebből a távolság kiszámítása). Több pulzár összehasonlításával kor szerinti megkülönböztetés.

Ismertnek tekintett alapfogalmak

Rák-köd, csillagközi anyag, diszperzió, elektromágneses sugárzás, mágneses tér, neutroncsillag, frekvencia, periódus, rádiósugárzás, fénysebesség. A neutroncsillagokról, mint szélsőséges tulajdonságú asztrofizikai objektumokról, egy magyar nyelvű leírást a http://vcssz.mcse.hu/cikk/var0001.html címen találunk.

Mérések

Jelek felvétele, periódus

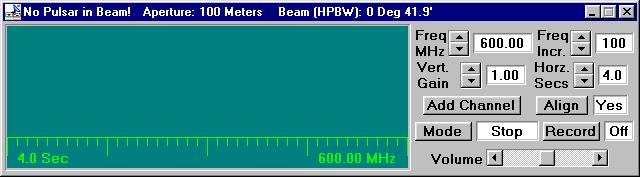
A  méréseket a CLEA észlelés-szimuláló programcsomag vonatkozó részével végezzük el (Linux alatt: Alt + F2, majd Pulzar.sh). Első lépésként belépünk a szimulációs felületre (Login). A File menü Run alpontjában kiválasztjuk a Radio Telescope pontot, amire az alábbi képet kapjuk:

A vezetés bekapcsolása után (Tracking) a Hot List menüből választhatjuk ki a mérendő objektumokat (a gyakorlaton három objektumot fogunk megvizsgálni). A kérdéses neutroncsillag beállítását követően a Receiver kapcsolóval juthatunk a vevőhöz:

Ennél a pontnál álljunk meg, és tanulmányozzuk a különböző kapcsolók (Record, Mode, Freq. Vert Gain, stb.) hatását! Szabadon próbálkozhatunk, a mért adatokat ugyanis elmenthetjük fájlba, vagy törölhetjük a memóriából. Ha felvettük a pulzár jeleit, egyszerű leolvasással megbecsülhetjük a pulzár periódusát:

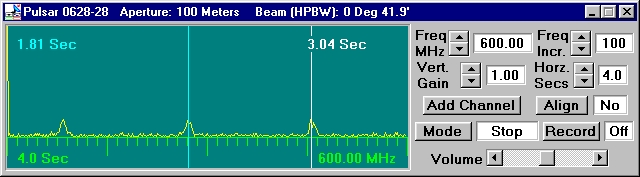
Az egymást követő jelek között eltelt idő helyett több ciklus időkülönbségével pontosíthatjuk a periódust. Ezek után megvizsgáljuk, hogy hogyan függ a pulzár periódusa a frekvenciától. Ehhez több csatornát meg kell nyitni (Add Channel), amelyek frekvenciáit sorra beállítjuk 400, 600, 800, 1000, 1200 és 1400 MHz-re. Hasonló módon megvizsgálhatjuk a jelek intenzitásának függését a frekvenciától (l. később).

A pulzár távolsága a jelek diszperziója alapján

Jól ismert, hogy míg vákuumban az összes elektromágneses hullám terjedési sebessége azonosan a fénysebesség, addig valamilyen közegben fellép a diszperzió jelensége, azaz a hullámhosszfüggő törésmutató miatt nagy távolságokon jelentősen szétválnak az eltérő frekvenciájú jelek. A csillagközi tér igen ritka anyagában az effektus igen kicsi, ám a több száz, esetleg ezer fényéves távolságokon már könnyen kimutatható. Az alacsonyabb frekvenciájú jelek akár több másodperc különbséget is összeszedhetnek a földi megfigyelőig tartó útjukon. Könnyen belátható, hogy a $V_a$ és $V_b$ sebességekkel mozgó jelek $T_A$ és $T_B$ beérkezési idejeinek különbsége egyértelműen megadja a befutott $L$ távolságot, az alábbi alakban:

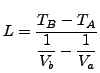$$L = \frac{T_B - T_A}{\dfrac{1}{V_b} - \dfrac{1}{V_a}}$$ (1)

Ezek után ,,csak'' a csillagközi anyag diszperziós formuláira van szükség, hogy a mért időkből következtessünk az éppen megfigyelt pulzár távolságára. Az elektromágneses sugárzás töltött részecskékkel való kölcsönhatását leíró elmélet szerint a frekvenciafüggő $v$ terjedési sebesség az $f$ frekvencia négyzetétől és a csillagközi anyagban fellépő $n_e$ elektronsűrűségtől függ, a következő módon:

$$v = \frac{f^2}{4150 \cdot n_e}$$

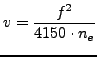
A gyakorlat során azt a független módszerekkel meghatározott távolságú pulzárok megfigyelésein alapuló feltevést használjuk, miszerint $n_e$ állandó, értéke pedig minden irányban 0,03 e/cm$^3$. Így az $f$ frekvenciájú jelek terjedési sebessége:

$$v = \frac{f^2}{124,5}$$

Ezekkel a feltevésekkel élve a vizsgált pulzár $D$ távolsága a két, különböző frekvencián (f MHz-ben!) mért jel között fellépő időkülönbségből megállapítható:

$$D = \dfrac{T_2 - T_1}{124,5 \cdot \left( \dfrac{1}{f_2^2} - \dfrac{1}{f_1^2} \right) }$$

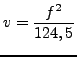
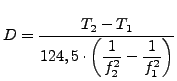
Feladatok

1. Indítsuk el a programot, majd ismerkedjünk meg a legfontosabb kezelőszervekkel!

2. Állítsuk be a Hot List menüpontból a 0628-28 jelű pulzárt! A vevővel vegyük fel 600 MHz-en a jeleit, amelyekkel gyakoroljuk a vevő megjelenítési lehetőségeit!

3. Határozzuk meg a 0628-28 pulzár periódusát 400, 600, 800, 1000, 1200 és 1400 MHz-en! Milyen frekvenciafüggést találunk és mire következtethetünk ebből?

4. Hogyan függ a jelek erőssége a frekvenciától? Ehhez állítsuk az összes csatorna vertikális erősítését 4-esre, majd válaszoljunk a következő kérdésekre:
   1. Kisebb vagy nagyobb frekvencián erősebbek a jelek?
   2. Ha pulzárok keresését tűznénk célul, mely frekvencia lenne az optimális?

5. Határozzuk meg a következő pulzárok periódusát: 2154+40, 0740-28, 0531+21 (a Rák-köd pulzárja)! Tudva, hogy a pulzárok öregedésükkel párhuzamosan lassulnak, soroljuk fel időrendben a három pulzárt!

6. Vezessük le az (1) összefüggést!

7. Állítsuk be ismét a 0628-28 pulzárt! A vevő első csatornáját állítsuk be 400 MHz-re, majd vegyük elő a második és harmadik csatornát is. A Mode kapcsolót Receive állásba téve folyamatosan vegyük a pulzár jeleit; a második csatornán 10 MHz-enként lassan lépdelve állapítsuk meg a jelek beérkezési idejének frekvenciafüggését! Ezek után a harmadik csatornát 800 MHz-re állítva határozzuk meg a pulzár $D$ távolságát (Mode $\rightarrow$ Stop)! Az adatokat felvéve (Record $\rightarrow$ On) részletesen is analizálhatjuk a méréseket speciális eszközzel (Analysis Window).