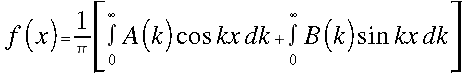 (1)
(1)2. Fourier sorok, Fourier transzformáció és az Airy-kép
Egy tetszőleges egy dimenziós, periodikus f(x) függvény kifejezhető szinusz és koszinusz függvények lináris kombinációjaként, ezt mondja ki a Fourier-tétel:
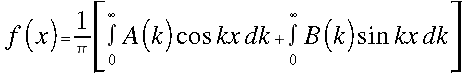 (1)
(1)
ahol A(k) és B(k) amplitúdók kifejezése a következő:
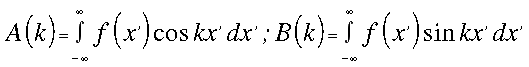 (2)
(2)
(2)-t
(1)-be történő
helyettesítésével
kapott kifejezésben felismerhető ![]() ,
vagyis (1) felírható csak koszinuszos
tagokból
(hiszen ezeket fázisban 90 fokkal eltolva szinuszt kapunk):
,
vagyis (1) felírható csak koszinuszos
tagokból
(hiszen ezeket fázisban 90 fokkal eltolva szinuszt kapunk):
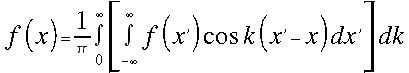 (3)
(3)
Mivel a koszinusz páros függvény, ezért (3) első integráljának határait átírhatjuk, illetve egyúttal az Euler-formulákat is felhasználva:
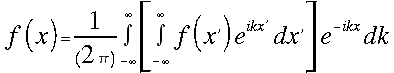 (4)
(4)
ami alapján a Fourier és inverz Fourier transzformáció képletei:
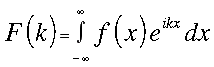 illetve
illetve 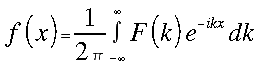 (5)
(5)
A transzformációt kiterjeszthetjük két dimenzióra is:
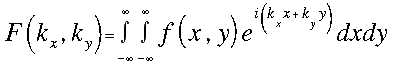 illetve
illetve 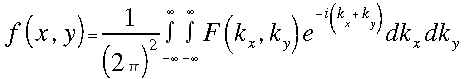 (6)
(6)
Vegyünk most egy kétdimenziós függvényt, pl. egy kör alakú apertúra intenzitáseloszlását:
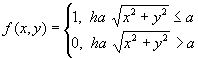 (7)
(7)
A (7) által definiált eloszlást "top hat", vagy kalapfüggvényként is nevezik (l. a kissé lejjebb lévő ábra felső részét). Bevezetve a következő változókat:
![]() ,
felírhatjuk a kalapfüggvény
Fourier-transzformáltját:
,
felírhatjuk a kalapfüggvény
Fourier-transzformáltját:
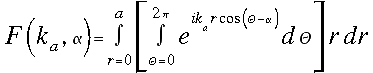 (8)
(8)
valamint
kihasználva a körszimmetriát, vagyis hogy ![]() -tól
nem függ (8), a következő alakot kapjuk:
-tól
nem függ (8), a következő alakot kapjuk:
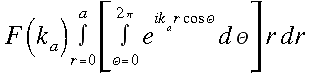 (9)
(9)
amiben
a nulladrendű Bessel-függvény alakját
fedezhetjük fel: 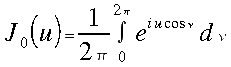 .
Ennek segítségével írva fel (9)-et:
.
Ennek segítségével írva fel (9)-et:
![]() új
változókat bevezetve:
új
változókat bevezetve:
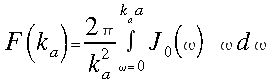 (11)
(11)
ami a különböző rendű Bessel-függvényekre vonatkozó sajátság alapján felírható elsőrendű Bessel-függvénnyel ilymódon:
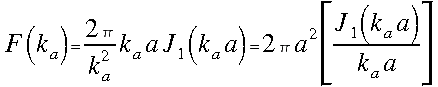 (12)
(12)
Ezt a formulát pedig már ismerjük, hiszen a Fraunhofer-féle diffrakciós egyenlet kör alakú apertúrára megoldva ugyanezt a végeredményt, az Airy-féle diffrakciós képet adta. Vagyis ezek szerint egy az apertúrától távol lévő ernyőn egy kivilágított nyílás diffrakciós képe nem más, mint az apertúra síkjában mérhető intenzitáseloszlás Fourier-transzformáltja.