Bevezetés 
Azok a fizikai rendszerek, amelyek abba a mérettartományba tartoznak, amely a mindennapokból ismerős makroszkopikus és az atomi mikroszkopikus skála közé esnek, több szempontból kiemelten érdekesek.
Ezeknek a mezoszkopikus rendszereknek a leírása fizikai szempontból a klasszikus és a kvantumos mechanika közötti átmenetet képviseli. A legtöbb esetben pusztán klasszikus megfontolások alapján nem jutunk a kísérleti tényekkel megegyező eredményre, ugyanakkor a szokásos kvantummechanikai módszerekkel sem lehet leírni a rendszert. Ez utóbbinak jellemzően az az oka, hogy a rendszer kölcsönhatása a nagyságrendekkel több szabadsági fokkal rendelkező környezettel azt eredményezi, hogy a kvantumos szuperpozíciók igen rövid időskálán megszűnnek létezni. Ilyenkor a kvantumos koherenciaképesség dinamikai eltűnéséről számot adó dekoherencia elmélet ad realisztikus leírást.
Az ilyen mérettartományba eső rendszerek közül sok ma már tervezhetően hozható létre, így az elméleti eredmények direkt mérésekkel ellenőrizhetők. Ezen túl a kísérletek –– különösen a félvezető illetve szilárdtestfizikai rendszereket illetően –– praktikus, azaz technológiai hasznosíthatóságot is ígérnek. Ez különösen igaz a spin szabadsági fokot érintő rendszerekre, mert a töltés mellett, azt kiegészítve, a spin iránya olyan plusz lehetőségeket hordoz, ami egy új típusú –– a spin szabadsági fokot információhordozóként használó –– elektronika, a spintronika alapjait jelenti. Elektronspinre, mint természetes kvantummechanikai kétnívós rendszerre, azaz qubitre gondolva, ez a gondolatmenet továbbvihető a sok lehetőséget rejtő kvantumos információfeldolgozás irányába is.
Más oldalról közelítve a kérdést, a kvantumos jelenségek megjelenése, megfigyelhetősége abban az esetben is várható, ha a vizsgált folyamat nem (vagy nem csak) térben, hanem az idő dimenziót tekintve is rövid. Ez az ultrarövid fény (lézer) impulzusok és az anyag kölcsönhatásának elméleti vizsgálatához jelenthet motivációt.

Eredmények
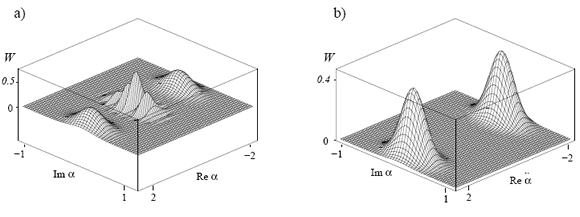
A '90-es évek végén kvantumoptikai rendszerek vizsgálatába kapcsolódtam be [1-4], később megkezdtük a spin szabadsági fok tanulmányozását szilárdtestfizika tárgykörébe tartozó modellekben [5-9]. A kvantumos szuperpozíciók eltűnését először kétnívós atomok rendszerében vizsgáltuk [1], kísérletileg megvalósítható javaslatot tettünk robusztus, úgynevezett dekoherencia-mentes állapotok létrehozására [2], majd szemléletes leírást adtunk Wigner függvény segítségével egy rezgő kétatomos molekula dekoherenciájára [3].
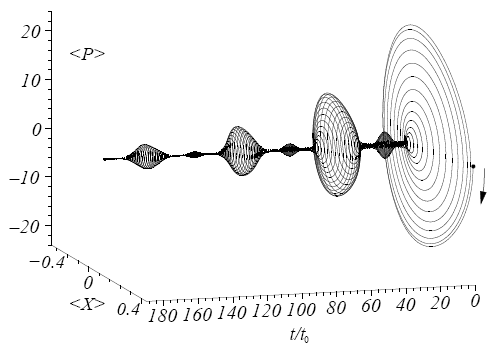
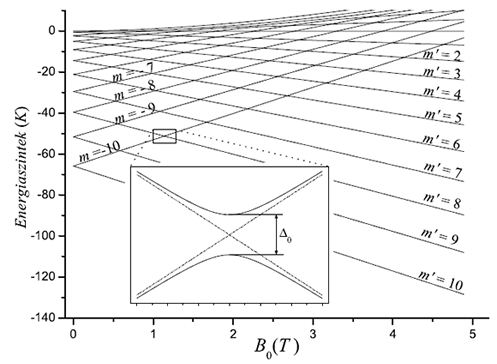
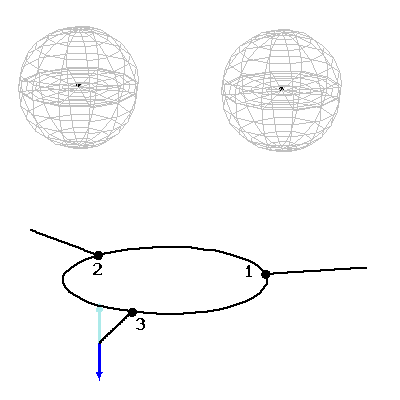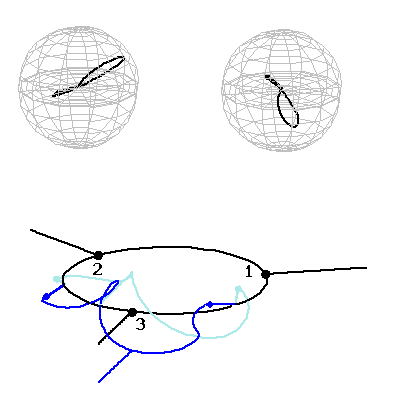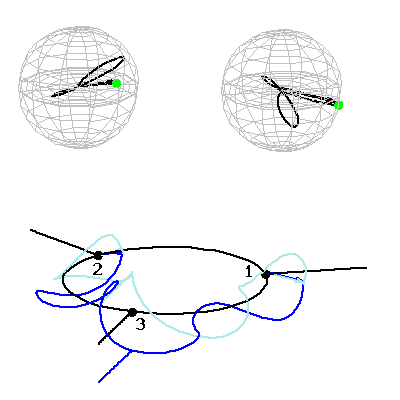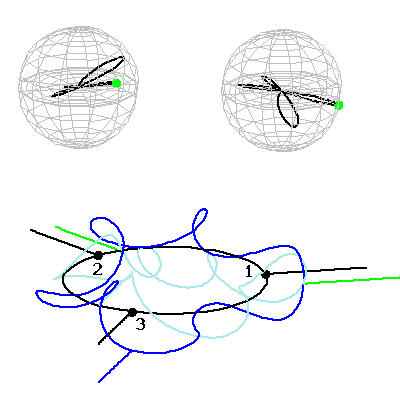
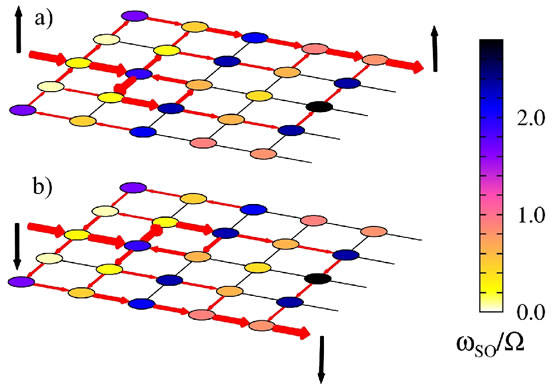
Ezek a tapasztalatok jó alapot szolgáltattak a spinnel kapcsolatos kutatásokhoz. E témában megvizsgáltuk, hogy a nagy (s=10) eredő spinnel rendelkező, molekulamágnesnek nevezett komplex molekulák kristálya hogyan hat kölcsön egy rezonátormódussal, miközben a spin szabadsági fok elkerülhetetlen dekoherenciát szenved el a rácsrezgésekkel való kölcsönhatás következtében. Rámutattunk, hogy a kísérleti úton tapasztalt THz frekvenciájú elektromágneses sugárzás [17] a legvalószínűbb esetben a mézerhez hasonló módon keletkezik [5]. Módszert dolgoztunk ki a spin szabadsági fok dinamikájának egzakt követésére gyorsan változó külső mágneses térben [6], megmutattuk, hogy bizonyos esetekben nem használható a szokásos kétnívós közelítés. Vezetési elektronok spinjének a lehetséges transzformációit mikrométeres átmérőjű félvezető gyűrűkben vizsgáltuk, megmutattuk, hogy a spin-pálya kölcsönhatás eredményeként az elektronspin iránya tervezhető módon elforgatható: alapvető kvantumos logikai kapuk realizálhatók ilyen módon [7]. Megmutattuk továbbá, hogy abban az esetben, ha az elektronok két vezetéken át is távozhatnak a gyűrűből, akkor a rendszer a Stern-Gerlach berendezéshez nagyon hasonló funkciót is elláthat, azaz polarizálatlan bemenő elektronok a kimeneteken már spinpolarizáltak lesznek, méghozzá a két vezetékben más-más irányban [8]. Vizsgáltuk ennek a jelenségnek a kapcsolatát a tér és a spin szabadsági fok kvantumos összefonódottságával is [9]. Számításaink szerint több gyűrű hálózatszerű összekapcsolása kiemelkedően gazdag spin transzformációs lehetőségeket rejt [10]. Kváziperiodikus struktúrk (szuperrácsok) esetén spinfüggő mini sávszerkezet áll elő [11], ami a vezetőképességet véges hőmérsékleten is észrevehetően befolyásolja [12]. Időben oszcilláló spin-pálya csatolás pedig pedig a kölcsönhatási régióból tovaterjedő spinpolarizált elektronhullámokat hoz létre [13].
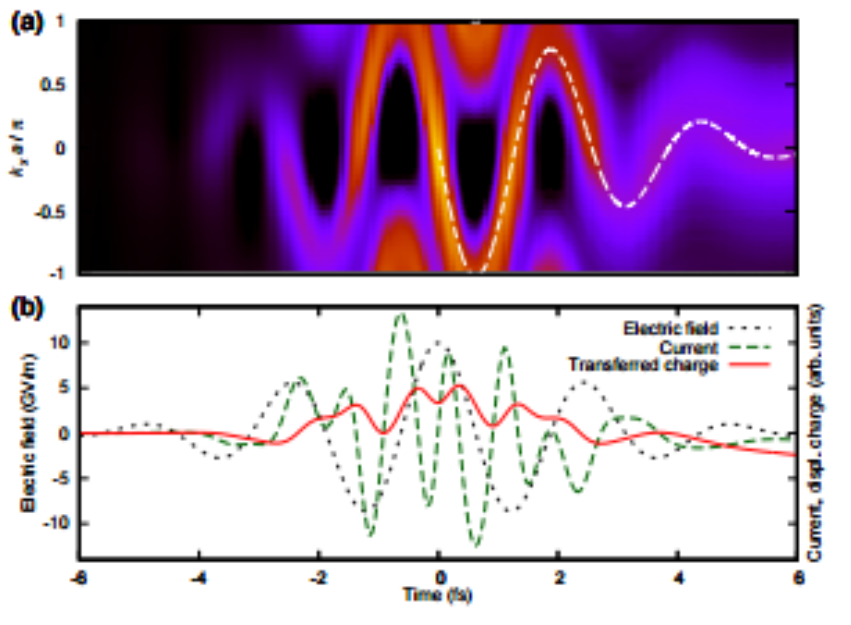
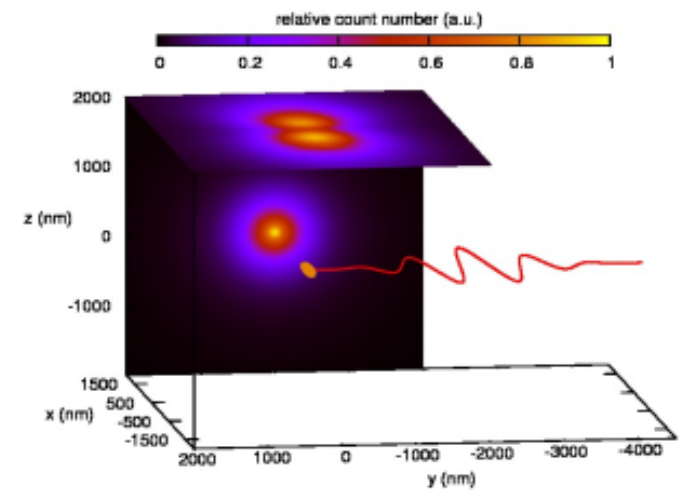
2011-től kezdve az időfüggő transzportfolyamatokkal kapcsolatos munkák kiterjesztéseként ultrarövid (néhány fs) lézerimpulzusok [16] keltette áramok leírásával [14] is foglalkozom, és általánosabban is, fontos területté vált számomra a rövid lézerimpulzusok anyaggal való kölcsönhatása [15].

Megválaszolandó (megválaszolható) kérdések
A kvantummechanika informatikai alkalmazásai szempontjából is ígéretes [12] molekulamágnesek kapcsán fontos a teljes a 21 energiaszinttel rendelkező rendszer dinamikai vizsgálata időfüggő külső mágneses térben a fononkörnyezet figyelembe vételével.

Vezetési elektronok spinjének manipulálásával kapcsolatban fontos a vezetékek nem-ideális csatolásának a vizsgálata, a véges szélesség figyelembe vétele, és elvi szempontból is érdekes annak a modellnek a kidolgozása, ami a lézerfény hatását írja le a vezetékekben található kétdimenziós elektrongázra.

A femtoszekundumos tartományba eső impulzushosszakkal rendelkező lézerfény és szilárdtestek kölcsönhatása jelenleg rengeteg nyitott kérdést tartogat még. Az elsődleges kérdés itt az időállandók összevetése, az egyes folyamatok fs időskálán vett jelentőségének a megítélése. Technikailag a félklasszikus Boltzmann egyenletnél pontosabb modell kidolgozása (pl. nem egyensúlyi folyamatokat leíró Green függvények alkalmazásával) a feledat.

Összefoglalva, a jelenlegi kutatás a kvantumoptikai és nyílt kvantumrendszerek leírásában szerzett tapasztalatokon alapul és részben folytatódik is ebben az irányban, ugyanakkor hangsúlyos a spinállapotok külső manipulálhatósága és a fény-anyag kölcsönhatás leírása a femtoszekundumos időskálán. A módszereket tekintve egymást kiegészítő analitikus és numerikus számítások a jellemzőek.

Hivatkozások
[1] P. Földi, A. Czirják, M. G. Benedict, Phys. Rev. A 63, 033807 (2001).
[2] P. Földi, M. G. Benedict, A. Czirják, Phys. Rev. A 65, 021802, (2002).
[3] P. Földi, M. G. Benedict, A. Czirják, B. Molnár, Phys. Rev. A 67, 032104 (2003).
[4] P. Földi, M.G. Benedict, T. Serenyi, A. Czirják, Fluct. Noise Lett.  4 (3): L511-L519 (2004)
[5] M.G. Benedict, P. Földi , F. M Peeters, Phys. Rev. B 72, 214430 (2005).
[6] P. Földi, M. G. Benedict, J. M. Pererira, F. M. Peeters: Phys. Rev. B 75, 2007.
[7] P. Földi, B. Molnár, M.G. Benedict, F. M. Peeters, Phys. Rev. B 71, 033309 (2005).
[8] P. Földi, O. Kálmán, M.G. Benedict, F. M. Peeters, Phys. Rev. B 73, 155325 (2006).
[9] O. Kálmán, P. Földi, M. G. Benedict, Open syst. & Inf. Dyn. 13, 455 (2006).
[10] P. Földi, O. Kálmán, M.G. Benedict, F. M. Peeters, Nano Lett., 8, 2556 (2008).
[11] P. Földi, V. Szaszkó-Bogár, F. M. Peeters, Phys. Rev. B 82, 115302 (2010.)
[12] P. Földi, V. Szaszkó-Bogár, F. M. Peeters, Phys. Rev. B 83, 115313 (2011.)
[13] V. Szaszkó-Bogár, F. M. Peeters, P. Földi, Phys. Rev. B 91, 235311 (2015.)
[14] P. Földi; M. G. Benedict,V. S. Yakovlev, New J. Phys: 15, 063019 (2013.)
[15] P. Földi,  I. Márton, N. Német, V. Ayadi, P. Dombi, Appl. Phys. Lett, 106, 013111 (2015.)
[16] A. Schiffrin et al, Nature 493, 70 (2013.)
[17] J. Tejada, E.M. Chudnovsky, J.M. Hernandez, R. Amigó, Appl. Phys. Lett. 84, 2373 (2004).
[18] M.N. Leuenberger, D. Loss, Nature 410, 789 (2001).

Schrödinger macska-állapot átmenete klasszikus keverékbe. Kvantumos harmonikus oszcillátor esetén léteznek különböző helyen lokalizált állapotok szoperozíciói, egy ilyennek a "fázistérbeli eloszlásfüggvényét" (Wigner függvény) mutatja az a) ábra. Ha a környezet csillapítja az oszcillátor amplitúdóját, végeredményül a két állapot klasszikus keverékét kapjuk, ez látszik a b) ábrán.

Letölthető cikkek
ArXiv link

.