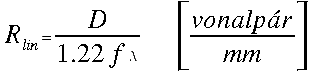 (1)
(1) 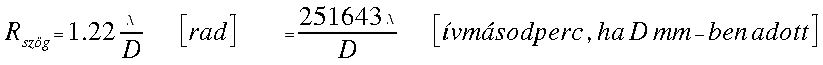 (2)
(2)3. Felbontóképesség és átviteli függvény, kontraszt
A Rayleigh-kritériumot már megismertük az Airy-kép levezetése során, itt most csak az eredményre hivatkozunk:
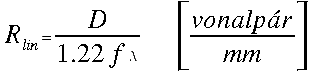 (1)
(1)
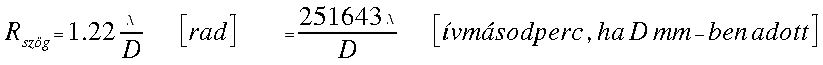 (2)
(2)
(2)-be
helyettesítve az 550 nm-es hullámhosszat az
amatőrcsillagász körökben közismert 138/D
kifejezést kapjuk a feloldóképességre.
Figyeljük meg, hogy az tulajdonképpen nem más,
mint az Airy-korong sugara, és ez hullámhosszfüggő!
Vagyis 656 nm-re már 165/D, 404 nm-re pedig 101/D
értéket
kapunk. A távcsőben megfigyelhető Airy-kép
tehát nem egyetlen gyűrűrendszer, hanem különböző
színű és paraméterű gyűrűrendszerek
összessége. Az emberi szem azonban 550 nm-en a
legérzékenyebb, így az ehhez tartozó
kép
a legerősebb, tulajdonképp ezt látjuk a relatíve
halvány csillagok esetén.
A Rayleigh-kritériumon
kívül más feloldási határokat is
értelmeztek és használnak, bár nem
egyenlő fényességű kettőscsillag-komponensek
esetén inkább csak a Rayleigh-kritérium
használatos. Az alábbi ábra szemlélteti a
Dawes és Sparrow kritériumokat, valamint a teljesen
feloldott esetet.
A felbontóképesség fenti értéke azonban csak ideális esetben érvényes. Amint a leképezés aberrációkkal terhelt, vagy központi kitakarása van a leképezőrendszernek, akkor az Airy-kép módosul, és ezzel együtt a feloldóképesség is. Ezt szemlélteti az alábbi ábra.
Amennyiben nem pontszerű forrásokra akarunk feloldóképességet értelmezni, sokkal nehezebb a helyzet. Egy vékony fekete vonal ugyanis világos háttér előtt beszürkül, egy fehér vonal sötét háttér előtt pedig kiszélesedik, legalábbis így látjuk. Egy szabályosan ismétlődő struktúra (vagy egy szabálytalan intenzitáseloszlású kép) esetén nagyon fontos, hogy a felbontani kívánt részletek között mekkora az intezitáskülönbség, ehhez pedig be kell vezessük a kontraszt fogalmát.
Kontraszt, kontrasztátviteli függvény (Modulation Transfer Function)
Nézzük az alábbi ábrát, ahol is a leképezendő objektum egy szinuszosan váltakozó intenzitást mutató vonalrendszer. A kép is hasonló lesz, csakhogy az intenzitásviszonyok megváltoznak.
Az objektum intenzitásértékeit I0-al, a képét I-vel jelölve a következőképp definiáljuk a kontrasztot:
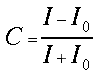 (3)
(3)
A kontrasztátviteli koefficiens azt mutatja meg, hogy az objektum két részlete közötti kontraszt a képen milyen kontraszttal jelenik meg, vagyis:
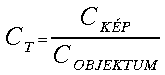 (4)
(4)
Az alábbi ábra 100%-os objektum-kontraszt és ideális optika esetén, aberrációk jelenlétében illetve a távcsövön belüli reflexiók (fényveszteség, szórt fény) esetén mutatja a kontrasztátviteli hányadost, illetve annak megváltozását.
Látható,
hogy ahogy az objektum egyre finomabb részleteit akarjuk
feloldani (a vízszintes tengelyen jobbra haladunk), úgy
egyre inkább csökken a kép kontrasztja (y
tengely). Ez azért van, mert az objektum egymáshoz igen
közeli egyes képpontjai a képen egymáshoz
igen közeli diffrakciós képként jelennek
meg, nem pedig képpontokként. A közeli
diffrakciós
képek fényszegényebb részeire a
szomszédos diffrakciós képek szórt
fénye
kerül, vagyis a diffrakciós képek
intenzitáskülönbségei, azaz a kontraszt
csökken.
A
kontrasztátviteli függvény (Modulation Transfer
Function, MTF) a kép felbontásának
függvényében
mutatja CT változását:
Látható az ábrán, illetve a következő táblázat mutatja, hogy a MTF-t nem csak az aberrációk, de a központi kitakarás is jelentősen módosítja, márpedig a legtöbb távcsőtípus rendelkezik központi kitakarással. Ezért a következőkben pár mondat erejéig visszatérünk a diffrakciós elmélethez.
|
kitakarás (%) |
0 |
25 |
50 |
|
Airy korong |
84 % |
73 % |
48 % |
|
első gyűrű |
7 % |
18 % |
35 % |
|
többi gyűrű |
9 % |
9 % |
17 % |
|
Airy korong átmérője (D mm-ben) |
280/D |
262/D |
230/D |
Tegyük
fel, hogy az a sugarú apertúrának a
közepén, az átmérő![]() -od
részéig terjedő szintén körszimmetrikus
kitakarás található. A 2. fejezetben (10)
ekkor úgy módosul, hogy nem 0-tól a-ig,
hanem
-od
részéig terjedő szintén körszimmetrikus
kitakarás található. A 2. fejezetben (10)
ekkor úgy módosul, hogy nem 0-tól a-ig,
hanem ![]() a-tól
a-ig végezzük el az integrálást:
a-tól
a-ig végezzük el az integrálást:
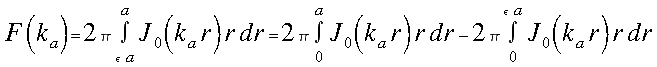 (5)
(5)
A megoldás teljesen hasonló módon történik, a végeredmény is hasonló, pusztán annyi a változás, hogy megjelenik egy negatív előjelű tag:
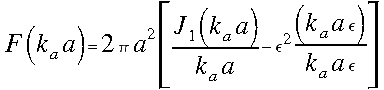 (6)
(6)
(6)-ot
ábrázolva látható, hogy ![]() növelésével egyre több fény kerül
a gyűrűkbe, vagyis a kontrasztátvitel hatékonysága
csökken:
növelésével egyre több fény kerül
a gyűrűkbe, vagyis a kontrasztátvitel hatékonysága
csökken:
Átviteli függvény, konvolúció, PSF
Még egy értelemben beszélhetünk átviteli függvényről, mégpedig az optikai rendszer képátviteli függvényéről. A különféle aberrációk ugyanis módosítják az ideális képet, vagyis a fókuszsíkban nem egy tökéletes Airy-féle kép jelenik meg egy pontszerű forrásról. Jellemezzük az optikai karakterisztikáját S függvénnyel, legyen a képet, illetve az objektumot leíró függvény K, illetve O. Tekintsük mondjuk az Airy-féle képet leíró függvényt O-nak, s egy dimenzióra szorítkozva a konvolúciós integrál:
![]() (7)
(7)
Ezt
az S fv-t nevezzük
pontforrás-eloszlásfüggvénynek
(Point-Spread Function, PSF), vagy másképpen
fogalmazva, a PSF az optikai rendszer válasza egy ![]() impulzusfüggvényre. Amennyiben nem pontszerű a
forrás, akkor is a PSF határozza meg a képet:
impulzusfüggvényre. Amennyiben nem pontszerű a
forrás, akkor is a PSF határozza meg a képet:
 (8)
(8)
A PSF-re, konvolúcióra később még többször visszatérünk, amikor a második félévben a digitális képfeldolgozásról, fotometriáról esik szó.
Lásd
Meteor Csillagászati Évkönyv 2004, Babcsán
Gábor cikkét az Amatőr távcsövek
teljesítőképességéről.
Innen letölthető...