5.1. Visszaverődés és fénytörés

A visszaverődés

Tekintsünk egy fénysugarat, amely egy közeg határfelületéhez érkezik. Ennek egy része onnan visszaverődik, reflektálódik. Kísérletileg azt találták, hogy a teljes energia visszavert hányada az anyag n törésmutatójától függ. Az intenzitásviszonyokat, melyek függnek a beeső fény polarizációs irányától, az ún. Fresnel-egyenletek (~1800.) írják le, melyeket itt nem részletezünk. A sugárzás visszaverődésének három típusát különböztetjük meg: irányított reflexió (tökéletesen sima felületeknél, pl. síktükörnél), szórt (diffúz) reflexió (durva reflektáló felületeknél, pl. vetítőernyőnél) és az irányított és a szórt reflexió keveréke. A visszaverődési törvény leírja a síktükörre beeső sugárzás menetét: a beeső és a visszavert fénysugarak és a beesési merőleges egy síkban vannak, a beesési és visszaverődési szögek egyenlők.

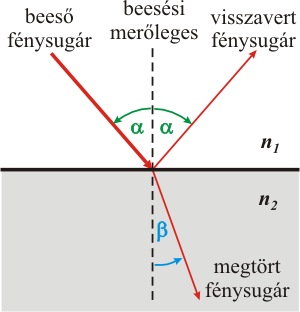
	5.1. ábra Fénytörés és visszaverődés

Az adott felület visszaverő- vagy reflexióképessége nem-polarizált sugarakra merőleges beesés esetén:

 .

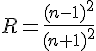A fénytörés

Ha egy sugár ferdén esik különböző törésmutatójú, áteresztő közeg határfelületére, akkor a határfelületen áthaladva a terjedés eredeti iránya megváltozik. Ez a refrakció (sugártörés). A megtört sugár és a beesési merőleges által bezárt szög a törési szög. Minél ferdébben éri a beeső sugár a határfelületet, annál nagyobb az irányváltozás mértéke. A határfelületet merőlegesen érő sugárnál fénytörés nem lép fel.

 A fénytörés jelenségét a Snellius-Descartes törvény írja le:  

,

ahol α a beesési, δ a törési szög, n₁ az első közeg törésmutatója, n₂ a törő közeg törésmutatója. A beeső és a megtört fénysugár egy síkban van. Optikailag ritkább közegből sűrűbb közegbe (n₁<n₂) lépve a sugár törése közelít a beesési merőlegeshez. Optikailag sűrűbb közegből ritkább közegbe lépve a sugár törése távolodik a beesési merőlegestől (n₁>n₂). Ha tehát a fény optikailag sűrűbb közegből halad a ritkább felé, a törési szög a beesési szögnél nagyobb érték lesz. Ezért ha a beesési szöget növeljük, elérhetünk egy olyan beesési szög értéket (amit α_o határszögnek nevezünk), amelyhez 90^o-os törési szög tartozik, azaz a fény már nem lép be az új közegbe, hanem a határfelületen halad tovább. Ha ennél is nagyobb beesési szöget veszünk, a fény a határfelületről a visszaverődés törvényének megfelelően visszaverődik. Mivel ilyenkor egyáltalán nem lép az új közegbe a fény, a jelenséget teljes visszaverődésnek (totális reflexiónak) nevezzük.

Az alábbi Interaktív animáció a fénytörés és visszaverődés szög-, illetve törésmutató függését szemlélteti, megmutatja a transzmissziós és reflexiós tényezőket az s és p irányban polarizált, illetve nem-polarizált fénysugarakra.