5. Törés- és visszaverődés síkfelületről
A probléma körvonalazása
Tegyük fel, hogy optikai szempontból két homogén és izotróp átlátszó közeget egy S felület választ el. A megfigyelések alapján tudjuk, hogy a határfelület felé tartó hullám a felülethez érve két hullámra bomlik. Ezen azt értjük, hogy megjelenik egy a felületről visszavert, illetve a másik közegbe átengedett hullám is.
A továbbiakban részletesen megvizsgáljuk a jelenséget arra az esetre vonatkozólag, mikor határfelület sík és a beeső fény síkhullámmal írható le (lásd a 3.4. a 3.5. és a 3.7. egyenleteket). A leírásnál fontos szerepet játszanak az 1. fejezetben ismertetett határfeltételek. A feladat megoldásához a Maxwell-féle egyenletek olyan megoldását kell megkeresni, amely teljesíti a határfelületre vonatkozó feltéteket is. Mivel az elektromágneses síkhullám megoldása a Maxwell-egyenleteknek és ezek lineáris egyenletek, kézenfekvő feltételezés, hogy a visszavert hullám is síkhullám. Így a beeső hullám felőli oldalon a beeső és a visszavert hullámok összege biztosan megoldása a Maxwell-egyenleteknek. Az átengedett hullámot szintén síkhullámmal próbáljuk leírni. Ezekkel feltételekkel a Maxwell-egyenletek mindkét közegben teljesülnek, és így ha a határfeltételeket is sikerül teljesíteni, akkor megtaláltuk a kitűzött probléma fizikai megoldását. Látni fogjuk, hogy a visszavert hullámra mindenképpen szükség van, ugyanis nélküle a határfeltételek teljesülése nem biztosítható!
A visszaverődés és a törés törvénye
Jelölje 
a beeső, 
a visszavert (vagy reflektált) és 
az átengedett (vagy transzmittált) elektromágneses síkhullám (3.4. a 3.5. és a 3.7. egyenletek) terjedési irányát. A számolás egyszerűsítése végett vegyük fel a vonatkoztatási rendszert úgy, hogy az S határfelület legyen a z = 0 egyenletű sík, és - általános ferde beesést feltételezve - felületre merőleges komponense a z, míg az érintő irányú komponense x tengely irányába mutasson. A beeső hullám terjedési iránya és a felületi normális által meghatározott sík a beesési sík, amely most a koordináta-rendszer speciális választása miatt a (z, x) sík. Legyen nb a közeg törésmutatója, cb a közegbeli fénysebesség a beeső hullám felőli (z < 0) oldalon, míg nt és ct a felület másik oldalán (z > 0).
Egy síkhullámot teljesen meghatároz egy adott pontban, mondjuk az origóban való időbeli lefutása. Ugyanis ha F(t) jelöli az origóbeli függést, akkor a 3.4. egyenletből az r = 0 miatt F(t) = E(ct) következik. Amiből tetszőleges r pontra F(t – s·r/c) = E(ct – s·r), amely a 3.4. egyenlet szerint éppen az E térerősség az r pontban és a t időben. Vagyis az F(t) függvény valóban meghatározza a síkhullámot. A határfelület r = (x, y, 0) pontjaiban a három síkhullámnak időben azonos módon kell változni, mert a határfeltételeknek minden időpontban teljesülniük kell. Ennek következtében a három síkhullám időfüggését meghatározó függvényeknek azonosaknak kell lenniük. Továbbá a z = 0 síkban lévő r = (x, y, 0) pontokra a
 |
(5.1) |
összefüggések állnak fenn. Amiből a vektorokat a koordinátáikkal kifejezve az
 |
(5.2) |
egyenlethez jutunk. Ezek az összefüggések tetszőleges (x, y) értékekre teljesülnek, ezért
 és  . |
(5.3) |
 |
|
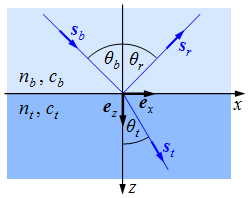
| 5.1. ábra. Síkhullám törése és vissza- verődése. A beesési síkbeli metszet. |
Mivel az (z, x) síkban van, azaz 
, így az előző képlet alapján
és 
.
Ami azt jelenti, hogy az és hullámnormálisok szintén a (z, x) síkban, vagyis a beesési síkban vannak. Így az 5.1. ábra jelöléseit használva
 , |
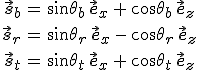(5.4a-c) |
ahol θb, θr és θt rendre a - beesési merőlegestől mért - beesési, visszaverődési és törési szögek. A vektorok x koordinátáit beírva az megfelelő 5.3. egyenletekbe:
 és  . |
(5.5a-b) |
Az 5.5. összefüggések a hullámnormálisokra vonatkozó állításokkal együtt a visszaverődés illetve a törés törvényeit adják. Mivel a szögek 0° és 90° közé esnek, a visszaverődésre θr = θb kapcsolat áll fenn.
Az 5.5b összefüggés Snellius-Descartes-féle törvény néven ismert, és az n = nt /nb hányadost - a fény terjedési irányát tekintve - a második közeg elsőre vonatkozó relatív törésmutatójának szokás nevezni. Ha n > 1, akkor a második közeget az elsőhöz képest optikailag sűrűbbnek, míg n < 1 esetben optikailag ritkábbnak mondjuk. A Snellius-Descartes-féle törvényből és a sin függvény monotonitási tulajdonságából következik, hogy a törési szög optikailag sűrűbb esetben kisebb, ellenkező esetben pedig nagyobb, mint a beesési szög. Ezért optikailag ritkább közegben a beesési szöget növelve, egy bizonyos határszögnél, a törési szög eléri a 90°-t. A beesési szöget ezen túl növelve az ú.n. teljes visszaverődés lép fel, amivel később részletesen foglalkozunk. Ekkor az 5.5b egyenletnek nincs valós megoldása.