A térmennyiségek viselkedése két közeg határfelületén
Bevezetés
A fény terjedése során gyakran előfordul, hogy a közeg optikai tulajdonsága egy határfelület mentén ugrásszerűen megváltozik. Ismert, hogy ilyenkor fényvisszaverődés és törés következik be. Számos optikai eszköz működésének a pontos leírásánál fontos a visszavert és az átmenő hullám amplitúdójának és fázisának az ismerete, a polarizációs viszonyok tisztázása. Ezen jelenségek elektromágneses fényelméleti leírásánál nagyon lényeges a térmennyiségek viselkedésének az ismerete a határfelületen való átlépéskor. A következő alfejezetben ezt a problémát vizsgáljuk meg.
Az elektromos eltolásra és a mágneses indukcióra vonatkozó feltételek
|
|
|
|
|
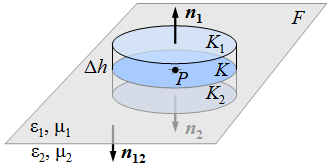
1.1. ábra. A felületre merőleges irányra vonatkozó határfeltételek vizsgálatánál alkalmazott henger. |
Tegyük fel, hogy a két különböző tulajdonságú térrészt az - 1.1. ábrán látható módon - az F felület választja szét. Vegyünk fel a felület P pontja körül egy Δh magasságú, a felülettel párhuzamos K2 alap- és K1 fedőkörlapokkal határolt hengert. A henger és a felület kör metszetét K jelöli. Erre a H hengerre fogjuk alkalmazni a harmadik illetve a negyedik integrális Maxwell-féle egyenletet úgy, hogy a henger Δh magasságát nullához tartatjuk. Az IM-3 egyenlet bal oldalán lévő elektromos eltolás fluxusát három tag, a felső K1 körlapra vonatkozó Φ1, az alsó K2 körlapra vonatkozó Φ2 és a palástra vonatkozó ΦΔh fluxusok összegére bonthatjuk, és így a
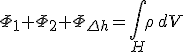
összefüggést kapjuk, ahol ρ a töltéssűrűség. Mivel az elektromos eltolás véges értékű, ezért a palástra vonatkozó fluxus eltűnik a henger magasságát minden határon túl csökkentve, hiszen az integrálási tartomány mértéke (a palást felülete) zérushoz tart. Így ΦΔh → 0 ha Δh → 0. A jobb oldalon lévő térfogati integrál - amely nem más mint a hengerben található töltés - pedig nyilván a P középpontú F felületen lévő K körlapon lévő felületi töltésmennyiségéhez tart, ha Δh → 0. Így az IM-3 egyenletet a Δh → 0 határátmenettel az
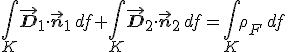 összefüggésre vezet, ahol ρF a felületi töltéssűrűség. Átrendezéssel az
összefüggésre vezet, ahol ρF a felületi töltéssűrűség. Átrendezéssel az
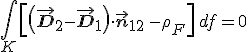
formulát kapjuk. Mivel a K körlap tetszőleges lehet - vagy akár ráhúzhatjuk a P pontra és az integrálszámítás középérték-tételét használva kapjuk, hogy az integrandus zérus, azaz
|
|
(1.9) |
ahol n12 a 1. közeg felől a 2. közeg felé mutató a felületre merőleges egységvektor. Mivel a n12 vektorral vett skaláris szorzatok a D1 és D2 vektorok felületre merőleges ![]() és
és ![]() komponenseit adják, így kimondhatjuk, hogy az elektromos eltolás merőleges komponense a felületen a felületi töltéssűrűségnek megfelelő ugrást szenved el, vagyis
komponenseit adják, így kimondhatjuk, hogy az elektromos eltolás merőleges komponense a felületen a felületi töltéssűrűségnek megfelelő ugrást szenved el, vagyis
|
|
(1.10) |
Amennyiben a felületen nincs töltés, úgy D merőleges komponense folytonosan megy át.
Teljesen analóg gondolatmenettel juthatunk el az IM-4 egyenletből kiindulva a mágneses indukció vektorra vonatkozó peremfeltételhez. Az eltérés mindössze annyi, hogy most a töltéssűrűséggel kapcsolatos tag hiányzik. Ezért a mágneses indukciónak a felületen való átmenetét a
|
|
(1.11) |
egyenlet adja meg. Ha ![]() és
és ![]() és jelölik rendre a B1 és B2 vektorok felületre merőleges komponenseit, akkor
és jelölik rendre a B1 és B2 vektorok felületre merőleges komponenseit, akkor
|
|
(1.12) |
Amit úgyis megfogalmazhatunk, hogy a B mágneses indukció merőleges komponense folytonosan megy át a határfelületen.
A mágneses és az elektromos térerősségekre vonatkozó feltételek
 |
|
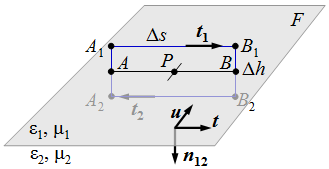
| 1.2. ábra. Az érintő irányú komponensekre vonatkozó peremfeltétel levezetésénél alkalmazott zárt integrálási útvonal. |
Az F felülettel párhuzamos komponensekre vonatkozó feltételek levezetéséhez alkalmazzuk az IM-1 egyenletet az 1.2. ábrán látható A1 → B1 → B2 → A2 → A1 zárt görbére, ahol az A1B1 és a A2B2 szakaszok a felülettel párhuzamosak, míg a A1A2 és a B1B2 a felületre merőleges Δh hosszúságú szakaszok. Amennyiben a mágneses térerősség véges értékű, Δh → 0 során a felületre merőleges szakaszokra a vonalintegrálok nullához tartanak, hiszen az integrálási tartomány mértéke (hossza) nullához tart. Ennek megfelelően H cirkulációjából a Δh → 0 során csak az érintőleges szakasz ad járulékot. Továbbá, ha az eltolási vektor idő szerinti deriváltja véges, akkor az A1B1B2A2 téglalapra az eltolási áramra vonatkozó járulék is eltűnik ha Δh → 0, hiszen most is az integrálási tartomány mértéke (a téglalap területe) zérushoz tart. Az áramsűrűséggel kapcsolatos tag a téglalapon átfolyó áramerősséget adja meg. A Δh → 0 esetben ez a tag az AB szakaszon átfolyó felületi áramnak az erőssége, melyet a JF felületi áramsűrűségnek az AB görbére merőleges (u irányú) komponensének az AB-re vett vonalintegráljából számolhatunk ki. Az elmondatottaknak megfelelően az IM-1 egyenletet a Δh → 0 határátmenetnél az
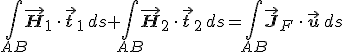
összefüggésre vezet. Mivel ![]() és
és ![]() , valamint
, valamint ![]() , az utóbbi egyenlet átrendezve a
, az utóbbi egyenlet átrendezve a
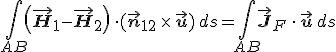
formulát nyerjük. Kihasználva a vegyes szorzat azon tulajdonságát, hogy a tényezőket ciklikusan permutálva az értéke nem változik meg, a baloldali integrált átírva az
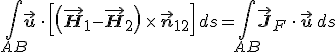
összefüggést nyerjük. Mivel az AB szakasz tetszőleges lehet, ezért maguknak az integrandusoknak kell megegyezniük, és így
|
|
(1.13) |
egyenlet áll fenn. Bontsuk fel H-t a felületre merőleges (n) és a felülettel párhuzamos (t) komponensekre: ![]() . Mivel
. Mivel ![]() , és így 1.13. egyenletből az
, és így 1.13. egyenletből az ![]() formulát kapjuk. Szorozzuk ezt meg jobbról vektoriálisan az n12 vektorral, és használjuk fel az ismert (a × b) × c = (ac)b − (bc)a vektor azonosságot, és így
formulát kapjuk. Szorozzuk ezt meg jobbról vektoriálisan az n12 vektorral, és használjuk fel az ismert (a × b) × c = (ac)b − (bc)a vektor azonosságot, és így
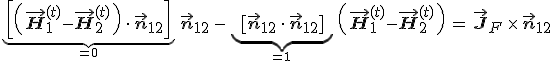 adódik. Az első szögletes zárójelben lévő skalárszorzat zérus, hiszen a két vektor merőleges, míg másodikban lévő pedig 1, mert n12 egységvektor. Így végeredményként a
adódik. Az első szögletes zárójelben lévő skalárszorzat zérus, hiszen a két vektor merőleges, míg másodikban lévő pedig 1, mert n12 egységvektor. Így végeredményként a
| (1.14) |
összefüggést kapjuk, amely azt mutatja, hogy a mágneses térerősség érintő irányú komponense a felületen való átlépéskor ![]() nagyságú ugrást szenved el. Amiből nyilván következik, hogy felületi áramok hiányában a mágneses térerősség érintőleges komponense folytonosan megy át.
nagyságú ugrást szenved el. Amiből nyilván következik, hogy felületi áramok hiányában a mágneses térerősség érintőleges komponense folytonosan megy át.
Az IM-2 egyenletből kiindulva az előzőhöz teljesen hasonló eljárással kapható meg az elektromos térerősségre vonatkozó peremfeltétel. A különbség mindössze annyi, hogy most az áramsűrűséggel kapcsolatos tag nem lép fel. Így, ha a mágneses indukció idő szerinti deriváltja véges, akkor az F felületen
|
|
(1.15) |
egyenlet áll fenn. Az elektromos térerősség ![]() felbontásával, a mágneses térerősség számolásánál látott módon adódik, hogy az elektromos térerősség érintő irányú komponense folytonosan megy át a határfelületen, azaz
felbontásával, a mágneses térerősség számolásánál látott módon adódik, hogy az elektromos térerősség érintő irányú komponense folytonosan megy át a határfelületen, azaz
| |
(1.16) |