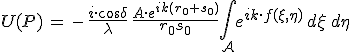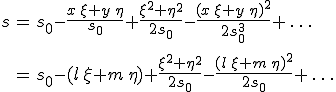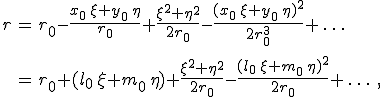Az elhajlási jelenségek osztályozása

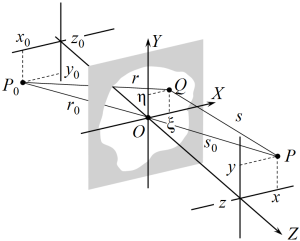
	10.8. ábra. Koordináta-rendszer a P0 pontból kiinduló, a z = 0 síkernyőn lévő nyílásokon áthaladó és elhajló monokromatikus gömbhullám vizsgálatánál.

Válasszuk meg a vonatkoztatási rendszert a 10.8. ábrán látható módon, vagyis úgy, hogy a nyílásokat tartalmazó ernyő síkja a z = 0 sík legyen. Tegyük fel, hogy a nyílás előtt a z = z₀ < 0 síkban lévő P₀ = (x₀, y₀, z₀) pontból egy - a 10.21. egyenlettel adott - gömbhullám indul ki. Keressük a nyílás mögött a z > 0 síkban lévő ernyő P = (x, y, z) pontjában a nyílásokon elhajló hullám térerősségét.

Az U(P) térerősség kiszámolására a 10.30. egyenletbeli első Rayleigh-Sommerfeld-féle diffrakciós integrált fogjuk használni, az és az az optikai tartományban jól teljesülő közelítést használva, ahol r₀ a P₀, és s₀ a P pont origótól mért távolságát jelöli. Ekkor

,

(10.33)

amely csak az inklinációs faktorban különbözik a 10.23. Fresnel-Kirchhoff-féle diffrakciós formulától. A számolás során az inklinációs faktor helyfüggése többnyire elhanyagolható, a χ (illetve a χ₀) szög kicsi, következésképpen az inklinációs tényező gyakran eggyel közelíthető mindkét diffrakciós formulában. Mi a számolás során az χ szöget a vektornak a Z tengellyel bezárt δ szögével, vagyis egy átlagos értékkel fogjuk helyettesíteni. Az inklinációs tényezőhöz hasonlóan a legtöbb esetben a nevezőben lévő r·s tényező Q-tól való függése is elhanyagolható, és így ez a tényező az r₀·s₀ állandóval közelíthető. Mindezeket figyelembe véve a 10.33. egyenlet az

(10.34)

alakba írható, ahol ξ és η a z = 0 síkban a Q integrálási pont koordinátái, továbbá az f(ξ, η) függvényt az

(10.35)

összefüggéssel értelmezzük. A 10.34. egyenletbeli integrandus a nyílás Q pontját mozgatva többnyire gyorsan oszcillál. Ezért az ilyen integrálok kiszámítása gyakran nem egyszerű feladat. Az oszcilláció miatt a nyílásnak csak olyan részei adnak jelentős járulékot az integrálhoz, melyeken az f függvény lassan változik - amit úgy fejezünk ki, hogy a fázis stacionárius. A nyílás többi részének a járuléka, a gyors oszcilláció miatt, gyakorlatilag elhanyagolható. Ezt felhasználva egy közelítő eljárást, a stacionárius fázis módszerét lehet kidolgozni [1].

Az

(10.36)

távolságot a sorfejtést használva a

(10.37)

kifejezéssel közelíthetjük, ahol

és

(10.38)

a P megfigyelési hely iránykoszinuszai ( és ). Hasonlóan közelíthetjük az

(10.39)

távolságot is:

(10.40)

ahol

és

(10.41)

a vektor, a nyílásra beeső fény irányát jellemző, iránykoszinuszai ( és ). A 10.37. és a 10.39. sorfejtéseket felhasználva, a 10.35. egyenlet alapján

(10.42)

kifejezést kapjuk.  A fényforrás és a megfigyelési hely olyan elrendezését amikor az f függvény már a lineáris kifejezéssel is jól közelíthető Fraunhofer-féle elhajlásnak nevezzük, illetve Fresnel-féle elhajlásról beszélünk, amikor a lineáris tag mellet már a másodrendű (vagy további magasabb rendű) tagokat is figyelembe vesszük. Gyakorlati szempontból igen fontos a nyíláson áthaladó konvergens gömbhullám esete, amely a fókuszálás, illetve általánosabban a képalkotás esetén fordul elő. A konvergens gömbhullám úgy tárgyalható a formalizmusunkkal, hogy a 10.33. diffrakciós integrálbeli exponensben r helyett -r változót írunk. A 10.36. formula alapján, ez pedig annak felel meg, hogy a 10.36, illetve azt követő  egyenletekben r₀-t negatívnak tekintjük. Ennek megfelelően Fraunhofer-féle elhajlás a következő, kétféle módon valósulhat meg:

1.

Ha a forrás és a megfigyelési hely egyaránt messze helyezkedik el az elhajlító ernyőtől, és a nyílás lineáris mérete is sokkal kisebb, mint ezek a távolságok, illetve pontosabban kifejezve, amennyiben teljesülnek az      és       feltételek, akkor 10.34. integrálban a négyzetes és a magasabb rendű tagok hatása elhanyagolhatók. A feltételek fennállta esetén 10.42. formula másodrendű tagjainak hatása mind elhanyagolhatók az és az egyenlőtlenségek miatt.

2.

A nyíláson elhajló konvergens gömbhullám esetén amennyiben fennállnak az    és     feltételek, akkor 10.34. integrálban a négyzetes (és a magasabb rendű) tagok hatása elhanyagolhatók. Ezek a feltételek képalkotás (fókuszálás) esetén állnak fenn, amikor a megfigyelési pont képsíkban (fókuszsíkban) a tengelyhez közel van.
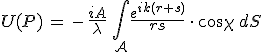