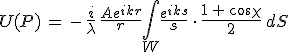Kirchhoff-féle diffrakciós integrál

	10.3. ábra. Az integrálási tartomány, és a jelölések értelmezése.

Tegyük fel, hogy a nyílásrendszer egy sík ernyőn helyezkedik el, melynek síkját a 10.3. ábrán Π jelöli. A szóba jövő problémáknál a tartomány nem véges, továbbá a 10.11. egyenletben az U függvényt és az irány szerinti deriváltját sem ismerjük. Ezen problémák kezelésére, vegyük körbe a P pontot egy R sugarú gömbbel, melynek a sugarát olyan nagynak választjuk, hogy a nyílások síkjával már legyen metszete. Jelölje a nyílás síkjának a gömbön belüli részét , a gömbfelület nyílások mögötti részét pedig . Alkalmazzuk a 10.11. egyenletet az felületre, és vizsgáljuk meg, hogy hogyan viselkedik az integrál az R → ∞ határátmenet során. Az integrált a két részfelületre felbontva az

(10.14)

összefüggéshez jutunk, ahol az integrálnak az  felületre eső részét I_Π, az  felületre vonatkozó

(10.15)

részét jelöli, ahol a formula felírásánál már figyelembe vettük, hogy a gömbfelületen s = R és az n felületi normális a vektorral azonos irányú és így cosγ = 1. Az integrál viselkedését érdemes most is az (R, θ, φ) gömbi polárkoordinátákat (P pontba helyezve az origót) használva tanulmányozni, ezekkel az integrál

(10.16)

alakba írható, ahol dΩ = sinθ·dθ·dφ az elemi térszög és Ω a teljes térszög (4π). Ebből az alakból már könnyen látható, hogy amennyiben megadhatók K és r₀ pozitív állandók úgy, hogy esetén

,   és

(10.17)

teljesülnek az ún. Sommerfeld-féle kisugárzási feltételek, akkor

.

(10.18)

Ezért, ha U teljesíti a 10.17. feltételeket, akkor R → ∞ esetén 10.14. egyenlet második tagja eltűnik, az első tag pedig a nyílásrendszert tartalmazó síkra vonatkozó integrálba megy át. így a nyílások síkja mögötti P pontban az

.

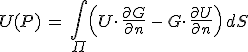(10.19)

adja meg a térerősséget. Amely azt mutatja, hogy a kisugárzási feltételek teljesülése esetén elegendő a nyílások síkjában ismerni a térerősséget és annak irány szerinti deriváltját. Ezeket azonban többnyire nem ismerjük. Erre vonatkozólag Kirchhoff a következő feltevéseket tette:

1.	U és ∂U/∂n nyílásbeli értékeit az ernyő jelenléte nem befolyásolja, így ezek megegyeznek a beeső hullám (nyílás nélküli) zavartalan terjedéséhez tartozó értékeivel.
2.	Az ernyő fedett részein U = 0 és ∂U/∂n = 0.

A Kirchhoff-féle határfeltételeket használva az integrálást csak a nyílásokra, azaz az ernyőnek az -val jelölt átlátszó részeire terjed ki. Így, ha G és ∂G/∂n 10.3. illetve 10.7. egyenletekkel adott értékeit explicit módon kiírjuk, akkor az ún. Kirchhoff-féle diffrakciós integrálhoz jutunk:

.

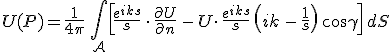(10.20)

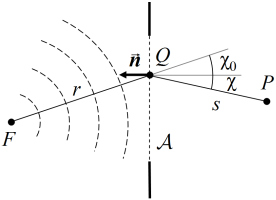
	10.4. ábra. A jelölések értelmezése az F pontból kiinduló gömbhullám esetén.

Ha a beeső hullám a nyílás előtti F pontból kiinduló

(10.21)

gömbhullám (10.4. ábra), akkor a 10.7. egyenlethez hasonlóan

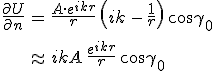(10.22)

kifejezés adja meg az irány szerinti deriváltat, ahol  (FQ szakasz hossza), γ₀ az  vektor és n felületi normális által bezárt szög. A 10.22. közelítés optikai hullámhosszakra többnyire nagyon jól teljesül, mert az r távolság sokkal nagyobb, mint a hullámhossz (), és így . Hasonló közelítést szokás alkalmazni a 10.20. formulában is, mivel gyakorlatban a megfigyelési hely s távolsága is több nagyságrenddel nagyobb, mint a hullámhossz. A 10.21. és 10.22. formulákat a 10.20. Kirchhoff-féle diffrakciós integrálba helyettesítve, és az említett közelítéseket alkalmazva az

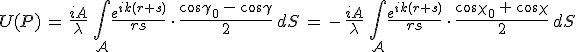(10.23)

Fresnel-Krichhoff-féle diffrakciós formulát kapjuk, ahol a χ és a χ₀ szögek gyakorlati szempontból könnyebben használhatók, az értelmezésüket a 10.4. ábra mutatja.

	10.5. ábra. Az F pontból kiinduló gömb- hullám nyílást kitöltő hullámfrontját W jelöli.

A nyílás pontjaiban a beeső hullám többnyire eltérő fázisban rezeg. Az ernyő síkja helyett más felületre is át lehet térni az integrálásnál, eddig a levezetésnél nem használtuk ki, hogy síkfelületre végezzük az integrálást. Sokszor célszerű az integrálási felületnek a beeső hullám fázisfrontját választani, amely gömbhullám esetén egy gömbfelület. Ebből az F pontból a nyílás pereméhez húzott egyenesek kivágnak egy darabot. Kirchhoff-féle határfeltételek esetén az integrált erre a nyílások által csonkolt hullámfelületre kell kiszámolni. A W hullámfelület és az ernyő pereme között lévő kúppalást járuléka többnyire kicsiny, mert egyrészt ez a felületdarab kicsi, mert általában a hullámforrás viszonylag távol van a nyílástól, másrészt ezen a felületdarabon a normális merőlegeshez közeli szögeket zár be az és a vektorokkal, így a szögek koszinusza is zérushoz közeli. Figyelembe véve, hogy a W hullámfelületen lévő pontokban χ₀ = 0 (mert γ₀ = π), így 10.23. egyenletből az

(10.24)

összefüggés adódik, melyet a Huygens-Fresnel-féle elv matematikai megfogalmazásának tekinthetünk. A 10.24. egyenlet szerint a P pontbeli térerősség a hullámfelület pontjaiból kiinduló elemi gömbhullámok szuperpozíciójaként áll elő. A hullámfelület Q pontja körüli dS nagyságú felületelem által kisugárzott elemi hullám amplitúdója arányos a beeső hullám Q-beli térerősségével, a felületelem nagyságával, a hullámhossz reciprokával és a megfigyelési iránynak hullámnormálissal bezárt χ inklinációs szögtől való függést kifejező

(10.25)

inklinációs faktorral, továbbá az elemi hullám fázisa π/2-vel késik a beeső hullám fázisához képest.