Fresnel-féle formulák
A visszavert és átengedett hullám
A továbbiakban feltesszük, hogy a közeg nem mágneses ![]() . A vizsgálódásunkat monokromatikus fényre szűkítjük le, valamint a szokásos komplex írásmódot alkalmazzuk. Ekkor a beeső (b), visszavert (r) és az átengedett (t) fényhullámok elektromos térerőssége rendre az
. A vizsgálódásunkat monokromatikus fényre szűkítjük le, valamint a szokásos komplex írásmódot alkalmazzuk. Ekkor a beeső (b), visszavert (r) és az átengedett (t) fényhullámok elektromos térerőssége rendre az
| (5.6a-c) |
alakba írhatók, ahol A, R és T komplex amplitúdó vektorok merőlegesek sorrendben a (nekik megfelelő) sb, sr és st hullámnormálisokra, továbbá
| (5.7a-c) |
 |
|
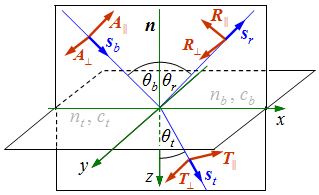
| 5.2. ábra. Síkhullám törése és visszaverődése. A beesési síkra merőleges (s) és a beesési síkban lévő (p) komponensek szemléltetése. |
Az térerősségeket célszerű felbontani a beesési síkra merőleges (s) komponens és a beesési síkban lévő (p) komponens összegére. Az s és p jelölés a német nyelv senkrecht (merőleges) és parallel (párhuzamos) szavaiból származnak. A p komponensek könnyen felírhatóságának céljából vezessük be az
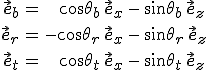 |
(5.8a-c) |
egységvektorokat, melyek a beesési síkban fekszenek és sorrendben merőlegesek az sb, sr és st hullámnormálisokra. Az utóbbi állítást könnyen ellenőrizhetjük az 5.4. egyenletek segítségével. Ezekkel már könnyen felírhatjuk az amplitúdók s és p irányú felbontását:
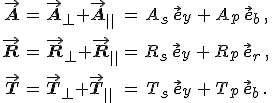 |
(5.9a-c) |
Az eddigiek alapján a beeső, visszavert és az átmenő fényhullámok térerősségeit
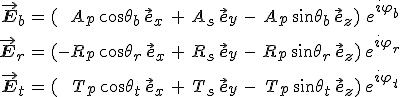 |
(5.10a-c) |
alakban írhatjuk fel. A 3.5. egyenletet alapján a mágneses térerősséget az elektromos térerősség és a hullámnormálisok meghatározzák, így a beeső, a visszavert és az átengedett fényhullámok mágneses térerősségeit a
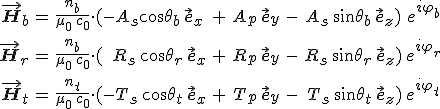 |
(5.11a-c) |
formulák írják le. Mivel a határfelületen nincsenek felületi töltések és nem folynak felületi áramok, így a határfeltételek szerint az elektromos és a mágneses térerősségnek a érintő irányú komponensei folytonosan mennek át a felületen, továbbá az elektromos eltolás és a mágneses indukció felületre merőleges komponense szintén folytonos a határfelületen. A határfelületen az 5.1. és a 5.7. egyenletek miatt φb = φr = φt , így θr = θb , az 5.10. és 5.11. összefüggésekből következőleg az x és y komponensek folytonossága megkövetelik a
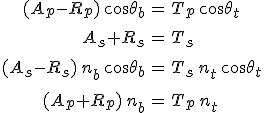 |
(5.12a-d) |
feltételek teljesülését. Könnyen látható, hogy amennyiben 5.12b és c teljesülnek, akkor az anyagegyenletek, a Maxwell-féle reláció és a Snellius-Descartes-törvény miatt, az eltolás és az indukció vektorok merőleges komponensére vonatkozó feltételek automatikusan teljesülnek. Látható, hogy 5.12. egy adott egyenletében vagy csak az s, vagy csak a p komponensekre vonatkozó mennyiségek szerepelnek. Ezért az egyenletek két egymástól független csoportra különíthetők el. Ami azt a fontos tényt mutatja, hogy az s és a p komponensek egymástól függetlenül terjednek.
A beeső hullám amplitúdóját ismertnek tekintve számoljuk ki a visszavert és az átmenő hullámokra jellemző amplitúdókat. Az 5.12a egyenletet nt-vel szorozva és levonva belőle az 5.12d egyenlet cosθt -szeresét Rp-re, továbbá az 5.12b egyenletet ntcosθt-vel szorozva és kivonva belőle 5.12c egyenletet Rs-re kapunk egyenletet. Ezeket az ismeretlenekre rendezve
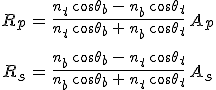 |
(5.13a-b) |
összefüggésekhez jutunk. Hasonlóan az 5.12a egyenlet nb-szeresét összeadva az 5.12d cosθb-szeresével Tp-re, míg az 5.12b egyenletet nbcosθb-vel szorozva és összeadva az 5.12c egyenlettel Ts-re kapunk egy-egy összefüggést, melyekből egyszerű számolással a
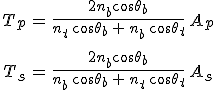 |
(5.14a-b) |
egyenletek adódnak. Az 5.13. és 5.14. egyenletek az ú.n. Fresnel-féle formulák.