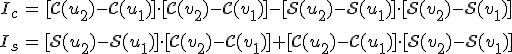Fresnel-elhajlás résen

	10.16. ábra. Résen történő Fresnel-féle elhajlás leírásánál használt koordináta-rendszer. Az X és Y tengelyek a rés éleivel párhuzamosak.

Legyen az elhajlító nyílás a 10.16. ábrán vázolt 2a × 2b élhosszúságú téglalap alakú rés. Az X és Y koordináta-tengelyeket irányítsuk a rés éleivel párhuzamosan. Ekkor a rés éleit az ernyő síkjában az ξ = ξ₁, ξ = ξ₂, η = η₁ és az η = η₂, egyenletű egyenesek adják meg. A 10.63. kettős integrálokat az

(10.75)

téglalapra kell kiszámolni. Az előző részben bevezettet K' és K koordináta-rendszerbeli koordináták között az

és

(10.76)

egyenletek állnak fenn, ahol ξ₀ és η₀ a Q₀ pont koordinátái. Ezt felhasználva a 10.71. integráloknál az integrálási tartomány

,

(10.77)

ahol

és        ,

(10.78)

j = 1, 2. A 10.73. integrálokat az

(10.79)

egyenletek adják meg, ahol és a Fresnel-integrálok. Az U(P) térerősség az I_c és I_s integrálok segítségével a 10.72. egyenlet alapján számítható ki. Érdemes megjegyezni, hogy a 10.79. kifejezésekben megjelenő különbségek grafikusan, a Cornu-spirálból könnyen leolvashatók. A Q₀ = (ξ₀, η₀) pontot mozgatva a z síkban lévő ernyőnek a 10.66. egyenletekkel adott pontjában kapjuk meg a térerősséget.

Az elhajlás szemléltetésére válasszuk azt az egyszerű esetet, amikor a fényforrás szimmetrikusan helyezkedik el a réshez képest, azaz legyen ,    és  . A 10.78. egyenletekkel értelmezett változók ekkor

és

(10.80)

alakba írhatók, ahol az

és

(10.81)

ún. Fresnel-féle számoknak szemléletes jelentés tulajdonítható. Látható, hogy N_a illetve N_b a rést a függőleges illetve vízszintes éleinél érintő hullámfrontokon a tengelyen a réstől d távolságra lévő pontból szerkeszthető Fresnel-féle zónák száma [1]. Ismert, hogy a zónákat úgy kapjuk meg, hogy a hullámfelületet d + mλ/2 sugarú a P középpontú gömbökkel felosztjuk (m = 1, 2, 3, …).

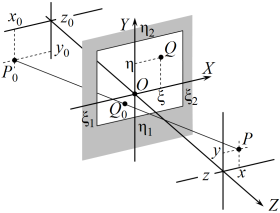
10.17. ábra. Intenzitás-eloszlás rés mögötti ernyőn Fresnel-féle elhajlás esetén. A fényforrás szimmetrikusan helyezkedik el a réshez képest. A piros grafikonok a tengelyek mentén szemléltetik az intenzitást. A szürke szaggatott vonalak a geometriai árnyék határát mutatják.

A 10.72. egyenletből számolt intenzitásokat a 10.17. ábra szemlélteti N_a = 5 és N_b = 8, illetve  N_a = 25 és N_b = 50 esetekre vonatkozólag. Az alkalmazásoknál gyakori eset, hogy egyik irányba, legyen most ez függőleges Y irány, a rés szélessége nagy. Ekkor N_b nagy szám, határesetben végtelennek tekinthető, így határesetben  a 10.79. kifejezésekben a koordinátákra vonatkozó különbségek 1-et adnak. Az elhajlási kép ekkor csak az koordinátától függ, ami azt jelenti, hogy a rés éleivel párhuzamos függőleges csíkokat kapunk. Ezeket a csíkokat szemlélteti a 10.18. ábrán látható animáció, amely során az N_a Fresnel-szám változik. Gyakorlati szempontból úgy valósítható meg, hogy az elhajlító nyílástól távolról indulva a megfigyelési ernyőt egyre közelebb visszük a nyíláshoz.

10.18. ábra. Intenzitás-eloszlás függőleges irányban nagyon széles rés mögötti ernyőn Fresnel-féle elhajlás esetén. Az animáció során az Na Fresnel-féle szám változik. Az intenzitás-eloszlást szemléltető kép felett az intenzitást ábrázoltuk a ξ0/a mennyiség függvényében. A geometriai árnyék határának a ξ0/a = ±1 értékek felelnek meg.