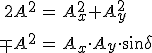Elfajult esetek

A monokromatikus síkhullám cirkulárisan poláros lesz A = B esetén, hiszen ekkor a polarizációs ellipszis egy A sugarú kör. Ennek a feltételét a 3.22. egyenletek segítségével könnyen meghatározhatjuk. Az A = B feltételt kihasználva a

egyenleteket kapjuk, ahol a felső előjel a balra, az alsó előjel a jobbra cirkulárisan poláros esetre vonatkozik.

Balra poláros esetben a második egyenletet 2-vel szorozva és az elsőhöz adva, elemi átalakításokkal az

egyenletet kapjuk, melyben az összeg mindkét tagja nem negatív. Így az összeg csak, akkor lehet nulla, ha a két tag egyszerre zérus, azaz A_x − A_y = 0 és 1 + sinδ = 0. Ezért annak a feltétele, hogy balra cirkulárisan poláros hullám alakuljon ki

és      ,

(3.33a-b)

ahol m egész szám.

Jobbra cirkulárisan poláros esetben 3.32. egyenlet első egyenletéből a második 2-szeresét levonva, egyszerű átalakításokkal az

formula adódik, ahol az összeg második tagját most is nem negatívnak tekinthetjük, mert jobbra poláros esetben sinδ > 0. Így jobbra cirkulárisan poláros monokromatikus síkhullám kialakulásának feltétele

és       ,

(3.34a-b)

 ahol m most is egész számot jelöl.

A polarizációs ellipszis egyenessé fajul B = 0 esetén. A 3.22. egyenletekből látszik, hogy ennek a feltétele

vagy       vagy   .

(3.35a-c)

Az első két feltétel azt a két nyilvánvaló esetet írja, amikor valamelyik komponens zérus. A harmadik feltétel akkor tejesül, ha

vagy     ,

(3.36a-b)

vagyis mikor a két komponens azonos, vagy ellentétes fázisban rezeg. A 3.15. egyenletekből könnyen megmutatható, hogy azonos fázisú komponensek esetén a 3.1. ábrán látható téglalap  egyenletű átlóján, míg ellentétes fázisú esetben az átlón rezeg, mindkét esetben amplitúdóval.

A lineárisan poláros síkhullámot szokták síkban polárosnak is nevezni, mivel a térerősségek a terjedési irányon átfektetett térben síkban rezegnek. Fizika történeti okok miatt, még az elektromágneses fényelmélet előtti időkből származó elnevezést megtartva, a mágneses térerősség irányát polarizációs iránynak, és ezt és a terjedési irányt tartalmazó síkot polarizációs síknak nevezzük. Az elektromos térerősséget és a terjedési irányt tartalmazó síkot rezgési síknak nevezzük. Sajnos a polarizáció bal vagy jobb forgási irányához hasonlóan, ezekben az elnevezésekben sem egységes a szakirodalom. Ez a bizonytalanság főként annak köszönhető, hogy az elektromágneses térelmélet szerint a fényt nem lehet egyértelműen leírni egyetlen úgynevezett fényvektorral. Ha az elektromágneses térnek a töltésekre gyakorolt

Lorentz-féle erőt tekintjük, akkor a 3.5. egyenletből következő

összefüggés miatt a mágneses tértől származó erőhatás a szokásos n törésmutatók éssebességek esetén több nagyságrenddel kisebb, mint az elektromos tértől származó erőhatás. Ezért sokszor az E elektromos térerősséget szokás fényvektornak tekinteni.