Fázisfelület és fázissebesség
A fázisfront mozgása. Fázissebesség
 |
|
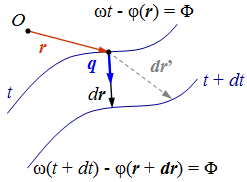
| 2.2. ábra. A fázisfront mozgá- sának szemléltetése. |
A térben azon pontok halmaza, melyekben egy adott t időpontban a monokromatikus hullám
| (2.21) |
fázisa állandó, egy felületet alkot. Ezt a felületet nevezzük fázisfelületnek vagy hullámfelületnek. Használatos még a fázisfront vagy hullámfront elnevezés is. Vegyük a t időpontban a Φ fázisértékkel adott fázisfelület, melynek pontjaiba húzott helyvektort r jelöl. Ahogy az idő telik a fázisfelület a térben mozog, a fázisfelület r vektorral adott pontjának a dt idő alatti elmozdulása legyen dr. Mivel a két fázisfronton a fázis értéke azonos, ezért az
![]()
összefüggés teljesül, ahol az utolsó átalakításnál a φ függvény lineáris közelítését alkalmaztuk. Amiből az
| (2.22) |
egyenlet következik. Legyen q vektor a dr elmozdulás irányába mutató egységvektor, és írjuk az elmozdulást dr = q·ds alakba, ahol ds az elmozdulás nagysága. Ekkor a ds/dt differenciálhányadost a
![]()
formula adja meg. A q vektor nyilván függ attól, hogy a két fázisfront pontjait hogyan feleltetjük meg egymásnak. Például a 2.2. ábrán látható dr és dr' is választható elmozdulásnak. Válasszuk q vektort úgy, hogy az így számított ds/dt minimális legyen. Ez akkor teljesül, ha a q vektor a φ gradiensének (![]() ) irányába mutat, hiszen a nevezőben lévő skalárszorzat ekkor maximális. Mivel a gradiens mindig merőleges a felületre, ez a választás annak felel meg, hogy a t és a t+dt (infinitezimálisan közeli) időpontokhoz tartozó fázisfrontok pontjait úgy feleltetjük meg egymásnak, hogy a t időponthoz tartozó fázisfelület pontjai a felületre merőlegesen mozdulnak el. Egy adott fázisfronthoz tartozó pont elmozdulása és így a sebessége is ekkor a legkisebb. Az előbbiek alapján
) irányába mutat, hiszen a nevezőben lévő skalárszorzat ekkor maximális. Mivel a gradiens mindig merőleges a felületre, ez a választás annak felel meg, hogy a t és a t+dt (infinitezimálisan közeli) időpontokhoz tartozó fázisfrontok pontjait úgy feleltetjük meg egymásnak, hogy a t időponthoz tartozó fázisfelület pontjai a felületre merőlegesen mozdulnak el. Egy adott fázisfronthoz tartozó pont elmozdulása és így a sebessége is ekkor a legkisebb. Az előbbiek alapján
![]() .
.
Az elmondottak szerint a fázisfelület mozgását olyan sebesség vektorral írhatjuk le, amely merőleges a fázisfelületre és a nagysága
| (2.23) |
A 2.23. egyenlettel definiált fizikai mennyiség a fázissebesség.