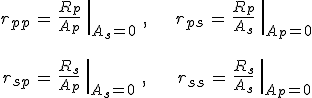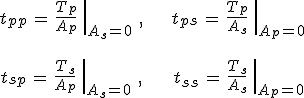Jones-mátrixok
A visszaverődésre vonatkozó Jones-mátrix
A 12.1. egyenletből a reflexióra vonatkozó Jones-vektor elemeit
|
|
(12.46) |
egyenletek adják meg, amiből látható, hogy a Jones-mátrix elemeit a
|
|
(12.47) |
összefüggésekből számíthatjuk ki. A 12.45. összefüggéseket kihasználva ebből a reflexiós Jones-mátrix elemei kiszámolhatók. Például nézzük az rpp elem kiszámítását: A 12.45. negyedik egyenletét a harmadikkal elosztva az
|
|
(12.48) |
összefüggéshez juthatunk. Az As = 0 feltétel miatt a 12.45. első egyenletéből a
|
|
(12.49) |
reláció következik. A mellékfeltételt kifejező 12.49. arányt a 12.48. egyenletbe írva az rpp mátrix elemet kapjuk eredményül. Teljesen hasonló módon kapjuk a reflexióra vonatkozó Jones-mátrix többi elemét is:
|
|
(12.50) |
A transzmisszióra vonatkozó Jones-mátrix
A rétegelt anizotróp közeg által átengedett fény és a beeső fény Jones-vektorai közötti 12.1. második összefüggését soronként kiírva az
|
|
(12.51) |
egyenleteket kapjuk. Így a transzmisszióra vonatkozó Jones-mátrix elemeit a
|
|
(12.52) |
relációkból számolhatjuk ki. A mátrix elemeket a reflexióhoz hasonlóan számolhatjuk ki. Például a tpp elem esetén a 12.45. negyedik egyenletét felhasználva
|
|
(12.53) |
relációt kapjuk. Ebbe az As = 0 mellékfeltételt kifejező 12.49. egyenletet helyettesítve kapjuk a keresett mátrix elemet. Teljesen hasonlóan adódik a többi transzmissziós Jones-mátrix elem:
|
|
(12.54) |