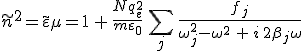A diszperzió Lorentz-féle modellje
A diszperzió Lorentz-féle modellje
A továbbiakban a diszperzió megjelenését egy egyszerű Lorentztől származó modell segítségével értelmezzük. Ez a modell egyszerűségének ellenére a gyakorlatban is jól használható összefüggést szolgáltat a komplex dielektromos állandóra és a belőle származtatott törésmutatóra.
Tegyük fel, hogy az atomokat (vagy molekulákat) csillapított oszcillátornak tekinthetjük, vagyis az elektronokra egy lineáris erő és egy sebességgel arányos csillapító erő hat. Ekkor az m tömegű, -qe töltésű, x helyvektorú E elektromos térben lévő elektron mozgását az
![]()
mozgásegyenlet írja le, ahol ![]() a lineáris erőre, míg k = m2β a csillapító erőre jellemző állandók, továbbá a mágneses térből származó erőt elhanyagoltuk. Tegyük fel, hogy a fény monokromatikus, így komplex írásmódot használva
a lineáris erőre, míg k = m2β a csillapító erőre jellemző állandók, továbbá a mágneses térből származó erőt elhanyagoltuk. Tegyük fel, hogy a fény monokromatikus, így komplex írásmódot használva
| (8.6) |
A térerősséget beírva a mozgásegyenletbe és a tömeggel osztva helyvektort a
| |
(8.7) |
egyenlet határozza meg, amely egy másodrendű lineáris konstans együtthatós inhomogén közönséges differenciálegyenlet. Ismert, hogy egy ilyen egyenletnek a megoldása előáll a homogén egyenlet általános megoldása és az inhomogén egyenlet partikuláris megoldásának az összegeként. A partikuláris megoldást keressük az
| (8.8) |
alakban, vagyis egy ω körfrekvenciájú harmonikus rezgés alakjában. Ezt a kifejezést a 8.7. egyenletbe helyettesítve egyszerű számolással kapjuk, hogy
| (8.9) |
A rezgéstanból ismert, hogy a homogén egyenlet időben csillapodó folyamatot ír le, így ez egy bizonyos idő után elhanyagolható a partikuláris megoldás mellett, így a tranziens folyamatok elmúltával
| (8.10) |
írja le az elektron mozgását. Így a beeső fény által egy atomban indukált dipólusmomentum
| (8.11) |
Ha a polarizálható atomok koncentrációja N, akkor
| (8.12) |
a polarizáció (dipólusmumentum-sűrűség). Mivel ![]() , ahol
, ahol ![]() a komplex elektromos szuszceptibilitás, így 8.12. összefüggés alapján
a komplex elektromos szuszceptibilitás, így 8.12. összefüggés alapján
| (8.13) |
Ennek következtében
| (8.14) |
a komplex relatív dielektromos állandó. A nevező komplex konjugáltjával szorozva a nevezőt és a számlálót is, egyszerű számolással az
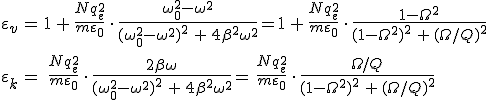 |
(8.15) |
összefüggések adódnak a valós és a képzetes részt meghatározó mennyiségekre, ahol ![]() és Q = ω0/(2β) dimenziómentes változók. Nem mágneses anyagot feltételezve μ=1, és így a 8.14. egyenlet alapján
és Q = ω0/(2β) dimenziómentes változók. Nem mágneses anyagot feltételezve μ=1, és így a 8.14. egyenlet alapján
| (8.16) |
kifejezésből számítható ki a komplex törésmutató. Ha az összeg második tagjának az abszolút értéke sokkal kisebb mint egy, akkor a ![]() alkalmazásával
alkalmazásával
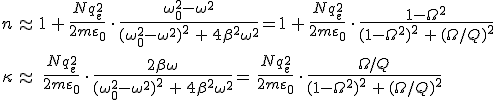 |
(8.17) |
 |
|
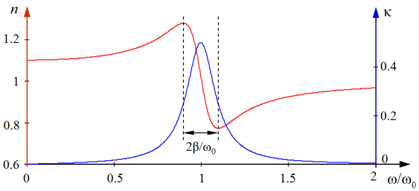
| 8.1. ábra. A törésmutató (n) és az elnyelési együttható (κ) frekvenciafüggése a Lorentz-féle modell alapján. |
közelítéseket kapjuk. A 8.1. ábra a Lorentz-féle modellből következő diszperziós görbe lefutását szemlélteti. A körfrekvenciát az ω0 rezonancia körfrekvenciához viszonyítottuk. Látható, hogy az elnyelést jellemző κ a rezonancia frekvencia környezetében jelentős, és az elnyelési sáv szélességét az 1/Q tényező adja meg. Normális diszperzióról beszélünk, ha n = n(ω) függvény növekedő (azaz dn/dω > 0), és anomális a diszperzió ha n = n(ω) csökkenő (azaz dn/dω < 0). Ha frekvencia helyett a vákuumbeli hullámhosszat használjuk független változóként, akkor deriváltak éppen ellentétes előjelűek. Látható, hogy jelentős elnyelés az anomális diszperziós tartományban van.
A modell könnyen általánosítható több rezonancia frekvenciával rendelkező rendszerre. Ha ωj és βj jelölik a rezonancia körfrekvenciákat illetve a velük kapcsolatos csillapítási tényezőket, akkor
|
|
(8.18) |
összefüggésből számítható ki a komplex törésmutató, ahol fj az ú.n. oszcillátor erősség, melyek összege egyenlő az atomban vagy a molekulában lévő, a folyamatban érintett elektronok Z számával ![]() .
.