Egytengelyű kristályok

Irányítsuk a koordináta-rendszer x₃ tengelyét úgy, hogy ez az optikai tengely irányába mutasson. Ekkor az x₁ és x₂ tengelyek irányába eső két fősebesség egyenlő (), és a   fősebesség ezektől eltérő. Ha bevezetjük az

egyenletekkel definiált sebességeket, akkor a fázissebességeket meghatározó 11.64. egyenlet az

alakba alakítható át. Amiből már könnyen kiszámítható a két fázissebesség:

ahol θ terjedési irány és az optikai tengely közötti szög (ezért és ). A dualitás szabályt alkalmazva a

egyenleteket kapjuk a két sugársebességre.

	11.11. ábra. Az index-ellipszoid és az elektromos eltolás rezgési irányai egytengelyű kristály esetén. Az elkészítésnél a kalcitnak megfelelő és adatokat használtuk. A terjedési irányt zöld vektor szemlélteti. Az optikai tengely az  tengely irányába mutat. A fősíkot világos kék szín jelöli.

Az index-ellipszoidot és a belőle következő rezgési irányokat a 11.11. ábra szemlélteti. Az optikai tengely és a terjedési irány által meghatározott síkot fősíknak, vagy főmetszetnek nevezzük. Mivel az ellipszoid hengerszimmetrikus a fősík szimmetriasík. Szintén a hengerszimmetria következtében tetszőleges s terjedési irányra merőleges központi ellipszis síkmetszet fősíkra merőleges tengelyének a hossza ugyanaz. Így a főmetszetre merőlegesen rezgő - ordinárius hullámnak hívott - hullám fázissebessége irányfüggetlen, összhangban a 11.67. első egyenletével. Az elnevezés arra utal, hogy ez a hullám az izotróp terjedés miatt szabályosan, az eddig megismert módon viselkedik a terjedés során. A főmetszetben lévő tengely hossza már függ az optikai tengely és a terjedési irány által bezárt szögtől. Ezért a főmetszetben rezgő - extraordinárius hullámnak nevezett - hullám fázissebessége már - a 11.67. második egyenletével leírt módon - függ a terjedési iránytól. Ha a fázissebesség irányfüggő, akkor a törésmutató is irányfüggő lesz. Ennek megfelelően ordinárius hullámra a törésmutató irányfüggetlen, míg az extraordinárius hullámra irányfüggő. Egy egytengelyű kristályt esetben pozitívnak,  teljesülésekor negatívnak nevezzük, amit két sebességre vonatkozó és  törésmutatókkal is ki szoktak fejezni. Így a kristály sorrendben pozitív, illetve negatív az , illetve relációk teljesülése esetén. A 11.11. ábrán látható kalcit (más néven mészpát) kristály index-ellipszoidjára 590 nm vákuumbeli hullámhosszra és . Ami alapján a mészpát negatív egytengelyű kristály.

A 11.67. és 11.68. egyenletekből látható, hogy a hullám- és sugárfelületek hengerszimmetrikusak az x₃ tengelyre vonatkozólag. Ezért a 11.10. ábrán is látható (x₂, x₃) síkbeli metszetgörbék egyértelműen jellemzik a forgási felületeket. A 11.10. ábra jelöléseit használva, gömbi polárkoordinátákkal a 11.67. egyenleteknek 

formulák felelnek meg. Az első nyilván egy sugarú gömb, a második pedig egy negyedrendű ovaloid, aminek a 11.10. ábra síkjába eső metszete az

egyenletű ovális. Gömbi polárkoordinátákkal a  11.68. egyenletek az

relációkkal fejezhetők ki. Az első egyenlet megint egy sugarú gömböt ír le. A második pedig egy olyan forgási ellipszoid egyenlete, melynek az optikai tengely irányába eső féltengelye , erre merőleges irányba pedig  hosszúságú. A sugárfelület (x₂, x₃) síkbeli metszetét az

egyenletű ellipszis írja le. A 11.71. ovális a 11.73. ellipszis talppontgörbéje. A sugár- és hullámfelületek metszeteit a 11.12. ábra szemlélteti. Az ábrán is látható, továbbá az előző alfejezetbeli vagy az ábra alatti interaktív animációval is könnyen ellenőrizhető, hogy ha a két sebesség közeli egymáshoz, akkor az ovális alig tér el az ellipszistől.

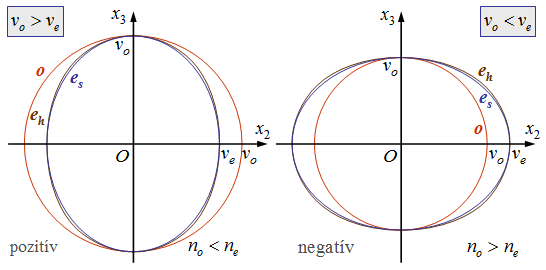11.12. ábra. Hullám- illetve sugárfelületek metszetei pozitív ( és ), illetve negatív ( és ) egytengelyű kristály esetén. Az ordinárius hullám (o) esetén a piros színnel szemléltetett hullám- és sugárfelület egybe esik. Az extraordinárius hullámra a kékkel jelölt sugárfelület (es) egy forgási ellipszoid, melynek metszete a 11.73. egyenletű ellipszis. A barnával jelölt hullámfelület (eh) egy forgási ovaloid, melynek metszete a 11.71. egyenletű ovális. Ha törésmutatók közötti különbség kicsi, akkor az ovális csak kicsit tér el az ellipszistől.

Az alábbi interaktív animáció a sugár- és a hullámfelületek (x₂, x₃) síkbeli metszeteit szemlélteti. Az n_o és n_e törésmutatók értéke csúszkával változtatható.