Monokromatikus síkhullámok

Amennyiben a 3.4. egyenletbeli általános E = E(u) = (E_x(u), E_y(u), E_z(u)) függvényt az

(3.14)

( j = x, y, z, és k = ω/c) alakban választjuk, akkor k·u = (ω/c)·(ct − s·r) = ω·[t − s·r/c] miatt, a gyakorlati és elméleti szempontból is különösen fontos, monokromatikus síkhullámhoz jutunk. Mivel az általános elektromágneses síkhullám transzverzális, azaz E és s merőleges vektorok, a leírás egyszerűsítése miatt célszerű a koordináta-rendszert úgy megválasztani, hogy valamelyik tengely, legyen ez a z tengely, az s egységvektor által adott terjedési irányba mutasson. Ekkor s = (0, 0, 1) és

,

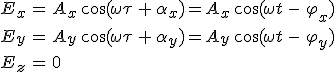(3.15)

ahol az A_x és A_y amplitúdók nem negatívak, τ = t − s·r/c = t − z/c, továbbá

és    .

(3.16)

A 3.15. egyenletből látható, hogy bármely r pontban a térerősség két merőleges és azonos frekvenciájú harmonikus rezgés összege. A BSc. képzésben tartott rezgésekkel vagy hullámokkal kapcsolatos alapkurzusokból is ismert, de a monokromatikus vektorhullámoknál a polarizációról elmondottakból is következik, hogy ekkor az E elektromos térerősség végpontja egy ellipszis mentén jár körbe, vagyis a monokromatikus síkhullámban E elliptikusan poláros hullám.

A mágneses térerősség a 3.5. és 3.15. egyenleteket felhasználva

amiből látszik, hogy H is elliptikusan poláros, azonban az amplitúdók és fázisok felcserélődnek, továbbá az amplitúdók skálázódnak és az x komponensre vonatkozó negatív előjel π fázistolással vehető figyelembe.

A következő interaktív animáció a polarizációs ellipszist szemlélteti. Az A_x és A_y amplitúdókat valamint az α_x és α_y kezdőfázisokat csúszkákkal állíthatjuk. A fázis értéke szintén (a kék) csúszkával állítható, az időbeli változás az Animálás jelölő négyzetbe kattintva indítható el.