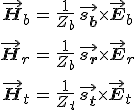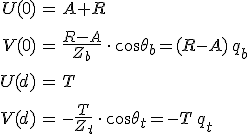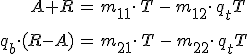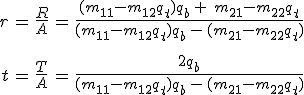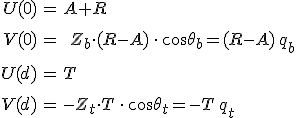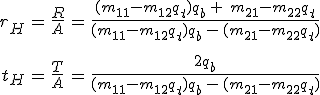Reflexiós és transzmissziós tényezők

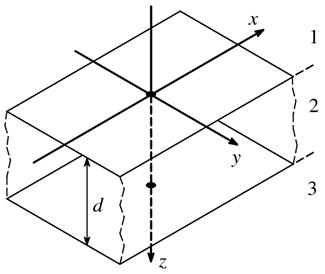
	6.1. ábra. A számolásnál alkalmazott koordináta rendszer. A lemez feletti (1),  és a lemez alatti (3) közeg homogén. A beesési sík az (x, z) sík.

Tegyük fel, hogy a z = 0 és a z = d egyenletű síkok közötti, mindkét oldalról homogén közeggel határolt, d vastagságú rétegezett közegre egy monokromatikus síkhullám esik a z < 0 tartományban θ_b beesési szöggel. Jelölje  ε_b és μ_b, valamint  ε_t és μ_t a lemez feletti (z < 0), illetve alatti (d < z) tartományban a relatív dielektromos állandót illetve a relatív permeabilitást, melyek már meghatározzák a n_b illetve n_t törésmutatókat. A beesési  szög és a lemez feletti közeg törésmutatója határozza meg az

mennyiséget, amely a terjedés során állandó marad. Már említettük, hogy ez a Snellius-Descartes-féle törvény általánosítása rétegelt közegre. Ez alapján fennáll a

egyenlet, amely lemezen áthaladó hullám terjedési irányát határozza meg. Mivel a lemez felett és alatt a közegek homogének, így a beeső, a visszavert és a lemezből kilépő síkhullámra is fennáll a 3.5. egyenlet, így az elektromos és mágneses térerősségek között a

relációk érvényesek, ahol Z_b a lemez feletti, Z_t a lemez alatti közeg hullámellenállásai és s_b, s_r és s_t rendre a beeső, a visszavert és az átmenő hullámok terjedési irányát megadó 5.4 egyenlettel definiált egységvektorok.

A továbbiakban kiszámoljuk z irányban inhomogén sík-párhuzamos lemez reflexiós illetve transzmissziós együtthatóit az s- és p-polarizációs állapotra vonatkozólag.

Vizsgáljuk először az s-polarizált hullám terjedését. Jelölje A, R és T sorrendben a beeső, a visszavert és az átmenő hullám elektromos térerősségének (komplex) amplitúdóit. A két határfelületen az elektromos és a mágneses térerősségek felülettel párhuzamos komponensei folytonosan mennek át. Ezért a 6.14, 6.15a és 6.61. egyenletek miatt fennállnak a

összefüggések, ahol q_b és q_t mennyiségeket a 6.58a egyenletből számolhatjuk ki az adott közegekre vonatkozólag. A 6.52. egyenlet szerint

kapcsolat áll fenn, ahol M a rétegezett lemez s-polarizációra vonatkozó karakterisztikus mátrixa. A 6.61. egyenletet felhasználva és a mátrix szorzást elvégezve a

egyenletrendszerhez jutunk, ahol m₁₁, …, m₂₂ az M(d, 0) karakterisztikus mátrix elemeit jelölik. Amiből az amplitúdókra vonatkozó reflexiós és transzmissziós együtthatókra az

formulák adódnak. A fényteljesítmények arányát megadó reflexiós és transzmissziós tényezőket a

összefüggések adják meg. A transzmissziós tényező kiszámolásánál figyelembe kell venni, hogy a lemez két oldalán a hullámellenállás különbözhet, továbbá a nyaláb keresztmetszete is megváltozik, ha a kilépő és a belépő fény terjedési irányai eltérőek.

Jelölje ezúttal A, R és T sorrendben a beeső, a visszavert és az átmenő hullámok mágneses térerősségeinek (komplex) amplitúdóit. A két határfelületen az elektromos és a mágneses térerősségek felülettel párhuzamos komponensei folytonosan mennek át. Így a 3.7 és a 6.23. egyenletek miatt fennállnak a

egyenletek, ahol q_b és q_t mennyiségeket a 6.58b egyenletből számolhatjuk ki az adott közegekre vonatkozólag. A belépési és a kilépési síkok közötti kapcsolatot a 6.52. egyenlet írja le, csak most a p-polarizációra vonatkozó karakterisztikus mátrixot kell használni. Mivel a 6.67. egyenletek azonosak az s-polarizációra vonatkozó analóg 6.62. egyenletekkel, így transzmissziós együtthatókra ugyanazt eredményt kapjuk:

Ne felejtsük el, hogy ezek a mágneses térerősségre vonatkoznak, amit a H indexszel jeleztünk. Az elektromos tér amplitúdóját a mágneses tér amplitúdójából, a 3.7 egyenletet szerint, a közegbeli hullámellenállással való szorzással kapjuk meg. A visszavert hullám a beesővel azonos, míg az átmenő ettől eltérő közegben terjed. Ezeket figyelembe véve, az elektromos térerősségre vonatkozó amplitúdó reflexiós és transzmissziós tényezőket a

összefüggések adják meg. A fényteljesítményekre vonatkozó tényezőket most is a 6.66. egyenletek szolgáltatják, csak itt a p-polarizációra vonatkozó q paramétert kell használni (lásd a  6.58b egyenletet).