Diffrakciós integrálok

Tekintsünk egy a

(10.1)

formulával leírt monokromatikus hullámot. Láttuk, hogy ez akkor és csak akkor megoldása a 2.7.  hullámegyenletnek, ha a térfüggést leíró komplex amplitúdó U(P) függvény kielégíti a 2.19. Helmholtz-féle egyenletet, vagyis

,

(10.2)

ahol k = ω/c a közegbeli körhullámszám, c a közegbeli fénysebesség. Könnyen megmutatható, hogy a

(10.3)

függvény, rögzített P pont mellett a Q pontot tekintve változójának szintén kielégíti a Helmholtz-egyenletet, ahol a P és Q pontok közötti távolságot jelöli. A 10.3. függvény a P pontban szinguláris, ettől a ponttól eltekintve jól viselkedő függvény. Fizikai jelentése pedig jól ismert: a P pontból kiinduló monokromatikus gömbhullámot ír le.

A matematikában szimmetrikus Green-tételként ismert tétel szerint, ha U és G függvények a korlátos tartományban és ennek szakaszonként sima  határán kétszer folytonosan differenciálhatók, akkor

,

(10.4)

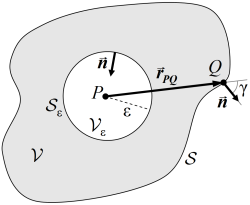
	10.2. ábra. Az integrálási tartomány, és a jelölések értelmezése.

ahol a tartomány határán a kifelé mutató felületi normális szerinti deriváltat jelöli. Alkalmazzuk ezt a tételt a 10.2. és a 10.3. egyenletbeli U illetve G függvényekre, egy a P pontot tartalmazó  tartományra, de mivel G szinguláris a P pontban, a tartományból ki kell zárnunk magát a P pontot. Tegyük ezt úgy, hogy a P pontot körbevesszük egy ε sugarú gömbbel, ahogy ezt a 10.2. ábra szemlélteti. Mivel U és G megoldásai a Helmholtz-egyenletnek, a tartományra a 10.4. Green-tételt alkalmazva az

(10.5)

összefüggést adódik, ahol . Mivel a két felületnek nincs közös része, az integrál a két felületre vonatkozó integrál összege, amiből az

(10.6)

egyenlet következik, ahol a I_ε jelölést az utolsó, ε sugarú gömbfelületre vonatkozó integrál rövid jelölésére vezettük be. Számoljuk ki a 10.6. egyenletben lévő G függvény irány szerinti deriváltját:

,

(10.7)

ahol γ a P-ből a Q-ba mutató vektor és a felület n normál vektora által bezárt szöget jelöli (10.2. ábra). Amennyiben a Q az ε sugarú gömbfelületen van , és így és . Ezeket és a 10.3. valamint a 10.7. összefüggéseket is figyelembe véve

.

(10.8)

Azt fogjuk megvizsgálni, hogy hogyan viselkedik ez az integrál az ε → 0 határátmenet során. Az integrált átírva az (ε, θ, φ) gömbi polárkoordinátákra, az

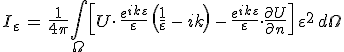(10.9)

alakot kapjuk, ahol az elemi térszög, és az integrál a teljes Ω térszögre (4π) vonatkozik. Ennek az előállításnak a nagy előnye, hogy az integrálási tartomány véges, és így a határértéket az integrálra vonatkozó középértéktétellel ki tudjuk számolni. Az integrandusban a zárójeleket felbontva látható, hogy a három tagú összeg első tagja U(P)-hez, a maradék kettő pedig nullához tart, ha ε → 0. Kihasználva, hogy az integrálási tartomány mértéke 4π, a középérték tételt alkalmazva

(10.10)

relációt nyerjük. Ezt a 10.6. egyenlettel összevetve az

(10.11)

összefüggést kapjuk. A G függvény (10.3) és az irány szerinti deriváltjának (10.7) a behelyettesítésével az

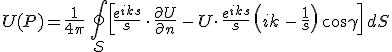(10.12)

formulához jutunk, amely Helmholtz-Kirchhoff-féle integrálformula néven ismert. Emlékeztetőül Q az S felület (általános) pontja, s a P és Q pont közötti távolság és γ az S felület Q pontbeli kifele mutató felületi n normálisa és a  vektorok által bezárt szög (10.2. ábra).

A 10.3. formulával értelmezett G(P,Q) függvény szinguláris a P pontban. A szingularitás olyan, hogy a 10.8. integrál, a 10.10. egyenlet alapján, véges határértékhez tart. Az ilyen viselkedés matematikai leírására vezették be az általánosított függvények (vagy disztribúciók) fogalmát. A G függvény különleges tulajdonságait a

(10.13)

disztribúciós egyenlettel fejezhetjük ki, ahol a Laplace operátor Q indexe azt jelöli, hogy az operátor a Q pont koordinátáira hat, továbbá δ Dirac-féle disztribúció. A 10.13. egyenlet megoldását a Helmholtz-egyenlet Green-féle függvényének nevezzük. Érdemes megjegyezni, hogy a definiáló egyenlet nem határozza meg egyértelműen a Green-függvényt. Ugyanis ha a G Green-függvényhez hozzáadjuk a (homogén) Helmholtz-egyenlet megoldását, ismét a 10.13. egyenlet egy megoldását, azaz Green-függvényt kapunk. Az elmondottak alapján a 10.3. függvény a Helmholtz-egyenlet egy Green-függvénye, és melyhez a homogén egyenlet megoldását hozzáadva, újabb Green-függvényhez juthatunk. Ezt a tulajdonságot később ki fogjuk használni. Érdemes azt is megemlíteni, hogy ha G a Helmholtz-egyenlet Green-függvénye, az egyenlet U megoldását a 10.11. formulával adhatjuk meg.
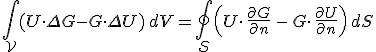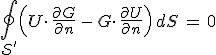
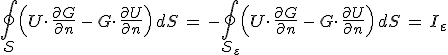
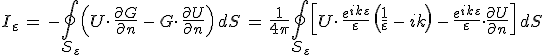