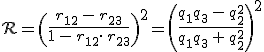Antireflexiós réteg
Reflexió csökkentés
A 6.76. egyenletből rögtön látható, hogy ha β értéke π értékkel növekszik vagy csökken, azaz a lemez vastagsága
|
|
(6.78) |
értékkel megváltozik, akkor az r reflexiós együttható változatlan marad, míg a t transzmissziós együttható csak előjelet vált, ahol λ0 a fény vákuumbeli hullámhossza. Mivel az átmenő fénynél fellépő előjel váltás hatása a teljesítményekre vonatkozó együtthatónál eltűnik, a 6.78. egyenletnek megfelelő vastagságváltozáskor a fényteljesítményekre vonatkozó együtthatók változatlanok maradnak. Ennek megfelelően a lemez vastagságát változtatva az ![]() és
és ![]() együtthatók Δd szerint periodikusan változik. A szélsőértékek ott vannak, ahol a 6.77a kifejezés Δ2 = n2·d változó szerinti deriváltja zérus. Ebből egyszerűn belátható, hogy a szélsőértékek helyét a
együtthatók Δd szerint periodikusan változik. A szélsőértékek ott vannak, ahol a 6.77a kifejezés Δ2 = n2·d változó szerinti deriváltja zérus. Ebből egyszerűn belátható, hogy a szélsőértékek helyét a
|
|
(6.79) |
feltételből számolhatjuk ki. Ebből adódik, hogy a szélső értékek a
|
|
(6.80) |
vastagságoknál vannak, ahol pozitív egész (m = 1, 2, 3, …). Páratlan m esetén ![]() , amiből 6.77a összefüggés alapján
, amiből 6.77a összefüggés alapján
|
|
(6.81) |
adódik, míg páros m esetén ![]() , amely
, amely
| (6.82) |
reflexiós tényezőt eredményez, ahol q paraméterekkel történő kifejezések származtatásánál a 6.72. összefüggéseket használtuk. Amiből látható, hogy páros m esetén a második közeg nincs befolyással a visszavert fény intenzitására, olyan mintha a második közeg nem is lenne ott. Hasonló állítás igaz ekkor az átmenő fény intenzitására is. A szélsőérték típusát a második deriváltból határozhatjuk meg. Megmutatható, hogy a második derivált előjelét
|
|
(6.83) |
a relációk határozzák meg, mégpedig a második derivált negatív a felső, és pozitív az alsó relációs jel esetén. Ennek következtében a felső reláció teljesülésénél a reflexiós tényező maximális, míg az alsó relációnál minimális. A 6.72. összefüggéseket felhasználva megmutatható, hogy
![]() .
.
Mivel a q paraméterek nem-negatívak, látható, hogy a 6.83. relációk ekvivalensek a
|
|
(6.84) |
relációkkal, amiből a törésmutatókat és a törési szögeket tartalmazó feltételeket kaphatunk 6.71. összefüggések segítségével. Az eddig elmondott általános következtetéseket a 6.3. ábra szemlélteti n1 = 1, n3 = 1,5 törésmutatójú közegek között lévő, az animáció során változó n2 törésmutatójú réteg esetén, merőleges beesést feltételezve. Ez megfelel a gyakorlatban fontos levegő-üveg határfelületre felvitt (vékony) rétegnek.
| 6.3. ábra. A reflexiós tényező n1 = 1, n3 = 1,5 és változó n2 törésmutató és merőleges beesés esetén. |
Az animációból látható, hogy az üvegre felvitt kisebb törésmutatójú réteggel (n2 < n3) a levegő-üveg felület 4%-os reflexiós tényezője csökkenthető, a legkisebb értékeket az
|
|
(6.85) |
optikai vastagságoknál kapjuk, ahol p pozitív egész. A 6.81. egyenletből következőleg az
|
|
(6.86) |
közbülső törésmutatóra a reflexiós tényező zérus lesz. Az animáción is jól látható, hogy a numerikus példa esetén ez ![]() törésmutatónál következik be. Az itt bemutatott eset fontos példa az úgy nevezett antireflexiós rétegre: a felületre felvitt vékony réteg(rendszer) segítségével a reflexiós tényező csökkenthető. Az 1,22 törésmutató túlságosan kicsi, gyakorlatban nehezen megvalósítható, ezért reflexió csökkentő rétegként leggyakrabban kriolitot (n ≈ 1,35), vagy magmézium-fluoridot (n ≈ 1,38) szoktak használni. Az animációból látható, hogy nagyobb törésmutatójú közbülső réteggel (n2 > n3) a reflexiós tényező növelhető, és a 6.85. egyenlet ekkor a maximumokat adja meg. A példánk azt is jól illusztrálja, hogy az
törésmutatónál következik be. Az itt bemutatott eset fontos példa az úgy nevezett antireflexiós rétegre: a felületre felvitt vékony réteg(rendszer) segítségével a reflexiós tényező csökkenthető. Az 1,22 törésmutató túlságosan kicsi, gyakorlatban nehezen megvalósítható, ezért reflexió csökkentő rétegként leggyakrabban kriolitot (n ≈ 1,35), vagy magmézium-fluoridot (n ≈ 1,38) szoktak használni. Az animációból látható, hogy nagyobb törésmutatójú közbülső réteggel (n2 > n3) a reflexiós tényező növelhető, és a 6.85. egyenlet ekkor a maximumokat adja meg. A példánk azt is jól illusztrálja, hogy az
|
|
(6.87) |
optikai vastagságokra a reflexiós tényező egyenlő a levegő-üveg határréteg 4%-os tényezőjével. Vagyis ekkor a réteg jelenléte nem befolyásolja a visszaverődést, összhangban már említett általános megállapítással, hiszen merőleges esetnél éppen a 6.87. feltétel felel meg a 6.80. egyenletbeli páros m értékeknek.