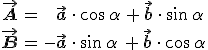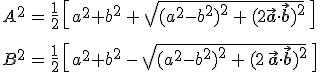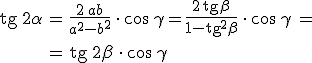Polarizációs ellipszis

A 2.45. egyenletet e^iα-val megszorozva, és a zárójeleket felbontva és a valós és képzetes részeket összevetve az

(2.48)

összefüggéseket kapjuk. Az α paraméter megválasztásával elérhető, hogy A és B vektorok merőlegesek legyenek. Ennek feltétele

,

(2.49)

amiből egyszerű számolással

,

(2.50)

és   .

(2.51)

A 2.48. összefüggésekből könnyen meghatározhatjuk az ellipszis féltengelyeinek a hosszát. A cos²α = (1 + cos 2α)/2 és a sin²α = (1 − cos 2α)/2 trigonometrikus összefüggéseket felhasználva

,

  

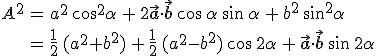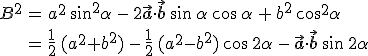
összefüggések nyerhetők. Így a 2.51. összefüggéseket felhasználva, egyszerű számolással az

(2.52)

egyenleteket kapjuk a féltengely hosszának négyzetére.

Jelölje ψ az a és a A vektorok által bezárt szöget (0 ≤ ψ ≤ 180°). A 2.45. egyenletet előbb A, majd B vektorokkal skalárisan szorozva, A és B merőlegességét figyelembe véve egyszerűen megmutatható, hogy

és      ,

(2.53)

amiből az a vektor A és B vektorokra vonatkozó vetületének iránya és velük bezárt szöge már könnyen kiszámítható. Mivel a·A/A = a·cos ψ, és a B vektorral bezárt szöget ψ szöggel kifejezve, a·B/B = ± a·sin ψ, amiből 2.53. összefüggéseit is felhasználva

(2.54)

egyenletet kapjuk, ahol a pozitív (+) előjelet kell használni, ha a-nak B-re vonatkozó vetülete B-vel ellentétes irányú, míg a negatív (−) előjel fordított esetben érvényes.

Ha γ jelöli az a és b vektorok által bezárt szöget, és bevezetjük a

definícióval a β segédszöget (0 ≤ β < 90°), akkor a 2.48. összefüggés a

(2.55)

formába írható át.

Attól függően, hogy a irányával szembe nézve a vektor az óramutató járásával ellentétes vagy megegyező irányba forog, balra illetve jobbra elliptikusan poláros hullámról beszélünk. A 2.46. egyenlet alapján, balra elliptikusan poláros esetben jobbsodrású, míg jobbra elliptikusan poláros esetben balsodrású vektorrendszert alkotnak. Ezt pedig egyszerűen eldönthetjük a vektorok vegyes szorzatának a segítségével: így a hullám balra vagy jobbra elliptikusan poláros ha az vegyes szorzat pozitív vagy negatív. Érdemes itt megjegyezni, hogy ezek az elnevezések a megfigyelő irányából nézve osztályozzák a forgási irányt. Sajnos a szakirodalom az elnevezésekben nem egységes, mert szokás még a forgási irányt pont ellentétesen, irányába (a forrás felől) tekintve osztályozni.

A következő interaktív animáció a polarizációs ellipszist szemlélteti.  A fázis értéke egy kék csúszkával változtatható. Az időbeli változást az Animálás jelölő négyzetbe kattintva indíthatjuk el. A jobb felső sarokban lévő ikonra kattintva a kezdeti paramétereket állíthatjuk vissza, ekkor azonban a csúszka animációs tulajdonsága kikapcsol. Ezt a jobb egérgombbal a csúszkára kattintva és az "Animálás be" menüpontot kiválasztva aktiválhatjuk újra. A fekete színnel rajzolt, a hullámot adott pontban leíró 2.43. egyenletbeli a és b vektorok végpontjait az egér segítségével mozgathatjuk. A program a 2.48. és 2.51. egyenletekből kiszámolja a főtengelyek irányába mutató A és B vektorokat és ezeket vörös, az ellipszist és F₁ és F₂ fókuszpontjait pedig zöld színnel ábrázolja.