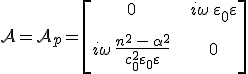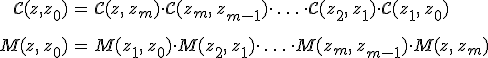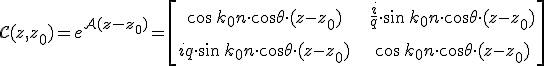Karakterisztikus mátrix
Rétegezett közeg karakterisztikus mátrixai
A kis matematikai kitérő után térjünk vissza a megoldandó optikai problémára. Mind az s-polarizált, mind a p-polarizált fény terjedését leíró 6.18. illetve 6.24. egyenletrendszer a
|
|
(6.48) |
alakba írható, ahol
|
|
(6.49a-b) |
s- illetve p-polarizáció esetén, továbbá
|
|
(6.50) |
Ha a térerősségek z függését meghatározó ![]() vektornak a z = z0 síkbeli kezdeti értékeket
vektornak a z = z0 síkbeli kezdeti értékeket ![]() jelöli, akkor az előző alfejezetben elmondottak szerint
jelöli, akkor az előző alfejezetben elmondottak szerint
|
|
(6.51) |
adja meg a 6.48. egyenlet megoldását, ahol ![]() az egyenletrendszer Cauchy-féle mátrixa. A reflexiós és transzmissziós tényező kiszámításánál ezen reláció inverze
az egyenletrendszer Cauchy-féle mátrixa. A reflexiós és transzmissziós tényező kiszámításánál ezen reláció inverze
|
|
(6.52) |
szükséges. Az 6.51. egyenlet és a Cauchy-mátrix inverzére vonatkozó 6.33. tulajdonság alapján
|
|
(6.53) |
Az M mátrixot a rétegezett rendszer karakterisztikus mátrixának nevezzük, mert ismeretében az s- vagy p-polarizációjú monokromatikus fény terjedését le tudjuk írni, és így M mátrix rendszer az optikai tulajdonságokat meghatározza. A teljes leíráshoz nyilván két, s- illetve és p-polarizációs állapotokat leíró Ms illetve az Mp karakterisztikus mátrix ismerete szükséges, melyeket a 6.49. egyenlettel adott ![]() illetve
illetve ![]() mátrixok határoznak meg.
mátrixok határoznak meg.
Ha a z0 és z síkok közötti rendszert ![]() síkokkal (m+1) darab részrendszerre bontjuk, akkor a rendszer Cauchy- illetve karakterisztikus mátrixa a részrendszerek megfelelő mátrixainak szorzatával kiszámítható, ugyanis a 6.32. tulajdonság miatt az
síkokkal (m+1) darab részrendszerre bontjuk, akkor a rendszer Cauchy- illetve karakterisztikus mátrixa a részrendszerek megfelelő mátrixainak szorzatával kiszámítható, ugyanis a 6.32. tulajdonság miatt az
|
|
(6.54) |
összefüggések állnak fenn.
Szakaszonként homogén rétegezett közeg
Az alkalmazások szempontjából különösen fontos eset az, amikor a rétegrendszer szakaszonként homogén. Ilyen rétegrendszert a bevezetőben is említett vákuum párologtatási eljárással lehet készíteni. Homogén közeg esetén a 6.49. egyenlettel értelmezett ![]() mátrixok állandók, így egy homogén alréteg Cachy-mátrixa a 6.39. formulával számítható ki.
mátrixok állandók, így egy homogén alréteg Cachy-mátrixa a 6.39. formulával számítható ki.
Számoljuk ki a Cauchy-féle illetve a karakterisztikus mátrixot homogén közeget feltételezve. Az α állandót célszerű
|
|
(6.55) |
alakba felírni, mert az így értelmezett θ szöggel a formulák egyszerűbbek lesznek. A mátrix exponenciális kiszámolásához első lépésben az ![]() mátrix sajátértékeit kell kiszámítani. Ezt a 6.49. egyenletbeli mátrixok esetén elvégezve, azt látjuk, hogy a két mátrix sajátértékei megegyeznek. Egyszerű számolással ezekre a
mátrix sajátértékeit kell kiszámítani. Ezt a 6.49. egyenletbeli mátrixok esetén elvégezve, azt látjuk, hogy a két mátrix sajátértékei megegyeznek. Egyszerű számolással ezekre a
|
|
(6.56) |
összefüggések adódnak. A Cayley-Hamilton-féle tételen alapuló eljárást követve, a 6.43. egyenletrendszert megoldva,
|
|
(6.57) |
kapjuk a Cauchy-mátrixra, ahol az s- és p-polarizációs állapot csak a q paraméterben különbözik:
|
|
(6.58) |
rendre s- illetve p-polarizáció esetén, ahol Z közeg hullámellenállása. A réteg karakterisztikus mátrixa a Cauchy-mátrix inverze. A 6.57. egyenletbeli mátrix inverzét kiszámítva
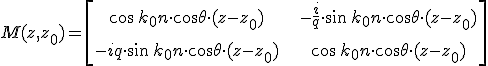 |
(6.59) |
formulát nyerjük a homogén réteg karakterisztikus mátrixára.
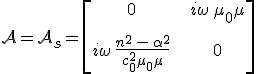 és
és