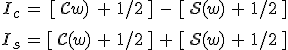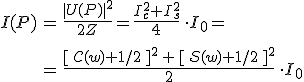Fresnel-elhajlás élen

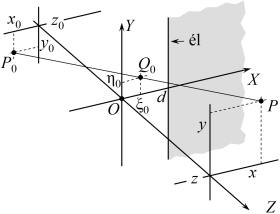
	10.19. ábra. Élen való Fresnel-elhajlás leírásánál használt koordináta-rendszer. Az elhajlító félsík élével párhuzamosan irányítjuk az Y tengelyt.

Legyen az elhajlító akadály egy átlátszatlan félsík, melynek az éle a ξ = d helyen van, ahogy azt az 10.19. ábra szemlélteti. Ekkor a diffrakciós integrált az

tartományra kell kiszámolni. Ebből látható, hogy ez a probléma a résen való elhajlás ξ₁ = –∞, ξ₂ = d, η₁ = –∞ és η₂ = +∞ eseteként fogható fel. Így 10.78. egyenleteknek megfelelően

továbbá

Amiből a 10.79. integrálokra az

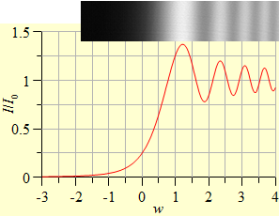
	10.20. ábra. Fresnel-féle elhajlási kép, és az intenzitás a w paraméter függvényében.

összefüggések adódnak. Ezekből az U(P) térerősség a 10.72. egyenletből számítható ki, amiből az intenzitásra az

egyenlet adódik, ahol I₀ a nyílás nélküli, zavartalan terjedéshez tartozó intenzitás. A 10.86. formulából számolt intenzitást a 10.20. ábra szemlélteti. A görbe felett látható kép egy kísérlet során CDD kamerával rögzített intenzitás-eloszlást mutat. Jól látható, hogy a megfigyelt csíkrendszert milyen jól visszaadja a számolás. A geometriai árnyékhatárnak a w = 0 paraméter felel meg. Az ábrából látható, hogy ezen a helyen az intenzitás negyede a nyílás nélkül kialakuló intenzitásnak.