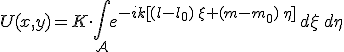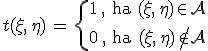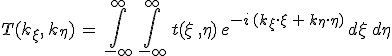Fraunhofer-féle elhajlás

Fraunhofer-féle elhajlás esetén a 10.34. integrál kiszámolásánál az

(10.43)

kifejezés használható, ahol az l, m és l₀, m₀ iránykoszinuszokat a 10.38. és a 10.41. egyenletek adják meg. Az 1. típusú Fraunhofer-féle elhajlás esetén, mivel a forrás távol van a nyílástól, a beeső hullámot síkhullámnak tekinthetjük. Az első kettő, l₀, m₀ iránykoszinusz már meghatározza a beeső síkhullám terjedési irányát, mert az iránykoszinuszok négyzetösszege 1. Hasonlóan, mivel a megfigyelési hely is távol van a nyílástól, a nyílás pontjaiból kiinduló elemi hullámok szintén síkhullámoknak tekinthetők. Az adott irányba az elhajlított hullámot ilyen síkhullámok szuperpozíciójaként kaphatjuk meg, amit a 10.34. egyenletből kapható

(10.44)

kifejezés fejez ki matematikai formában, ahol

.

(10.45)

A 2. típusú Fraunhofer-féle elhajlást pedig szemléletesen úgy képzelhetjük, hogy a síkhullámnak megfelelő párhuzamos fénysugarakat az ideális leképező eszköz a fókuszsíkjának az adott iránynak megfelelő pontjába gyűjti össze. Így a fókuszsík ezen pontja megfelel az adott irányban elhajló hullámnak.

A 10.44. egyenletbeli integrál matematikai szempontból egy kétdimenziós Fourier-transzformáció. Ha bevezetjük a nyílás 

(10.45)

ún. pupillafüggvényét, amely, mint látható egységnyi a nyílás nyitott pontjaiban és zérus a fedett részeken, akkor az integrálást ki lehet terjeszteni a teljes síkra, így a 10.44. egyenlet

(10.46)

az alakba írható, ahol

(10.47)

a t(x, y) függvény kétdimenziós Fourier-transzformáltja. A 10.46. egyenlet azt mutatja, hogy Fraunhofer-féle elhajlás esetén a térerősség egy szorzó tényezőtől eltekintve a nyílás pupillafüggvényének Fourier-transzformáltjával egyezik meg. A Fourier-transzformáltra vonatkozó Plancherel-tétel felhasználásával megmutatható, hogy ha a nyílásokra eső fényteljesítmény P_A, a nyílások felülete F, akkor

,

(10.48)

Z a közeg hullámimpedanciája, vagyis a K komplex állandó abszolút érték négyzetének energetikai jelentése van.