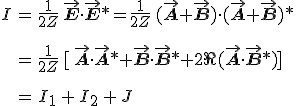Monokromatikus fény interferenciája

Tegyük fel, hogy két monokromatikus fényhullám találkozik a P pontban. A hullámok leírására komplex írásmódot fogunk használni, mert így az intenzitás könnyen kiszámolható. Az eredő hullám térerőssége a két hullám térerősségének összege:

,

(9.1)

ahol

és

(9.2)

a két találkozó hullám komplex amplitúdója, továbbá a derékszögű komponensek valós amplitúdóit a_j és b_j, fázisait α_j és β_j jelölik. Feltéve, hogy a két hullám síkhullámmal írható le a 3.13a egyenletet szerint az

(9.3)

formula adja meg az eredő intenzitást, ahol Z a közeg hullámimpedanciája,

és

(9.4)

a két találkozó hullám intenzitása és

(9.5)

 az ún. interferenciatag. Az  α_j és β_j fázisok általában különbözhetnek, azonban a kísérleti körülmények olyanok, hogy a komponensek fázisának különbsége általában ugyanaz a

(9.6)

érték, amit célszerű a két forrástól a megfigyelési pontig megtett optikai úthosszak különbségével kifejezni, azaz a

(9.7)

alakba írni, Δ az optikai úthosszkülönbség és a λ a vákuumbeli hullámhossz. A 9.6. formulát felhasználva az interferenciatag a

(9.8)

formában írható fel. A XIX. század első felében Fresnel és Arago kísérletekkel kimutatták, hogy két egymásra merőlegesen lineárisan polarizált fény esetén nem figyelhető interferencia. Ebből arra következtettek, hogy a fény transzverzális hullám. A 9.8. egyenlet alapján érhető, hogy miért nem jelentkezik ekkor interferencia. Legyen a két hullám terjedési iránya az x₃ tengely irányába, és rezegjen az egyik hullám az (x₁, x₃), a másik hullám az (x₂, x₃) síkban. Így az első hullámra a₂ = 0, a másik hullámra pedig b₁ = 0. Amennyiben a fény transzverzális hullám, úgy a₃ = b₃ = 0, és ennek következtében a

interferenciatag valóban eltűnik (J = 0). Így Fresnel és Arago megfigyeléseit a fény transzverzális természetének kísérletei bizonyítékának tekinthetjük.

Ha a két azonos irányban, például az x₁ tengely irányába rezgő lineárisan poláros hullámra a₂ = b₂ = a₃ = b₃ = 0. Ezt kihasználva a 9.8. egyenlet alapján az interferenciatag

(9.9)

alakban fejezhető ki. Amiből az interferencia következtében kialakuló intenzitást az

(9.10)

képletből számíthatjuk ki. A 9.10. egyenlet alapján mondhatjuk, hogy a két monokromatikus fényhullám maximálisan erősíti egymást, ha azonos fázisban találkoznak, azaz , ahol m egész, amit az interferencia rendszámának nevezünk. Az intenzitás maximumát

(9.11)

egyenlet adja meg. Továbbá, két monokromatikus fényhullám maximálisan gyengíti egymást, ha ellentétes fázisban találkoznak, azaz a fázisra a  feltétel teljesül. A minimális intenzitás

(9.12)

a képlet szolgáltatja. Amennyiben azonos intenzitású nyalábok interferálnak (), akkor maximális intenzitás az intenzitások négyszerese lesz, a minimális intenzitás pedig zérus. Azaz ekkor ellentétes fázisú találkozásnál a két hullám kioltja egymást. A 9.7. egyenlet alapján a maximális erősítés és gyengítés feltételét kifejezhetjük a két hullám közötti optikai úthosszkülönbséggel is. Könnyen látható, hogy maximális erősítés feltétele , míg a maximális gyengítés esetén teljesül.