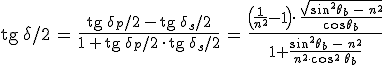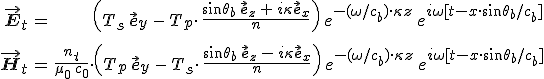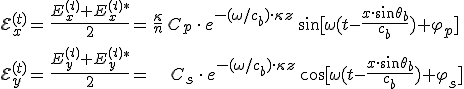Teljes visszaverődés

	5.4. ábra. Fénytörés és teljes visszaverődés víz-levegő határfelületen.

Az 5.4. ábrán látható kísérletben a fény vízből terjed levegőbe, vagyis optikailag sűrűbb közegből lép optikailag ritkább közegbe, a így töréshez tartozó relatív törésmutató egynél kisebb (n < 1). Ekkor

összefüggéssel meghatározott törési szög, a sin függvény [0, π/2] intervallumon növekedő volta miatt nagyobb a beesési szögnél, ahogy ez a kísérletnél is jól látható. A relációból következik, hogy az egyenletnek csak olyan beesési szögre van valós megoldása, amelyre

feltétel teljesül, ahol θ_h az ú.n. határszög. Az egyenletből látható, hogy a határszög az a beesési szög amelynél a törési szög 90°, és így

.

(5.21)

Ha beesési szög a határszög alatt van, akkor a törés a szokásos módon játszódik le, azonban a határszöget meghaladó beesési szögre a kísérletek szerint nem figyelhető meg átmenő fény, a teljes fényenergia visszaverődik a határfelületről.

Ha a beesési szög kisebb mint a határszög, vagy azzal egyenlő (), akkor egyenlet θ_t megoldása valós. Ezért a merőleges és határszög közötti beesés esetén a jelenség lefolyása az n > 1 esettel azonos jellegű. Azonban, ha a beesési szög nagyobb mint a határszög , akkor a θ_t gyök komplex. A Fresnel-formulákban fellépő cosθ_t mennyiséget kifejezhetjük   segítségével, ahol a két eset közül a negatív előjel a fizikai szempontoknak megfelelő gyök. Ugyanis az 5.6. és 5.7. egyenletből belátható, hogy az átmenő hullám a pozitív előjel esetén exponenciálisan növekedő, a negatív előjel mellett pedig exponenciálisan csillapodó amplitúdójú hullámot ír le. Ezek közül nyilván a csillapodó hullám, azaz a negatív előjel felel meg a kísérleti megfigyelésnek. Ezen megjegyzést figyelembe véve

,  ahol  .

(5.22)

Ezt beírva az 5.17. egyenletekbe az

és

(5.23)

összefüggéseket nyerjük az amplitúdókra vonatkozó reflexiós tényezőkre. Amiből jól látható, hogy a számláló és nevező egymás komplex konjugáltja, aminek következtében . Így a reflexiós tényezők exponenciális alakja

és       ,

(5.24)

ahol

és       .

(5.25)

Ezek az egyenletek azt mutatják, hogy a visszaverődés során mindkét komponensnél fázisugrás lép fel, amely azonban egymástól eltérő. Ennek következtében a párhuzamos és a merőleges komponensek között

(5.26)

fáziskülönbség keletkezik a teljes visszaverődés során. A tg(α–β) kifejezésre vonatkozó azonosság alkalmazva

(5.27)

összefüggést kapjuk, ahol az utolsó átalakításnál az 5.25. összefüggéseket helyettesítettük be. Egyszerű átalakításokkal a

(5.28)

formulát kapjuk a fáziskülönbségre (). Ebből látható, hogy a fáziskülönbség határszögnek megfelelő beesésénél (θ_b = θ_h), valamint súrlódó beesésnél (θ_b = π/2) zérus, a két eset között (θ_h < θ_b < π/2) pozitív. Az 5.5. ábra n = 1/1,6 = 0,625 esetén szemlélteti a reflexiós tényező amplitúdóját és argumentumát.

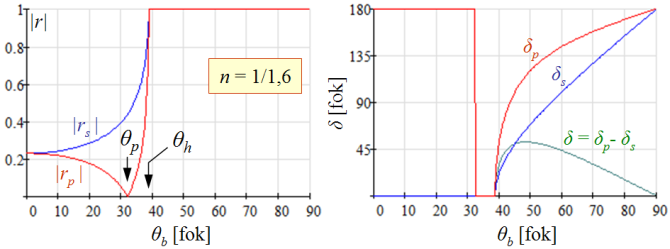5.5. ábra. Az amplitúdókra vonatkozó reflexiós együtthatók abszolút értéke (balra) és argumentuma (jobbra) n = 1/1,6 = 0,625 relatív törésmutató esetén. A Brewster-szög 32º, a határszög 38,68º.

	5.6. ábra. Fresnel-féle hasáb.

Jól látható, hogy Brewster-szögnél a párhuzamos komponens eltűnik, a visszavert fény ezért lineárisan poláros. Teljes visszaverődés során a két komponens között fáziskülönbség lép fel, ezt szemlélteti a zölddel rajzolt görbe. Erre a törésmutató értékre a fáziskülönbség két beesési szög esetén is eléri a 45º-ot, ami azért fontos, mert két egymást követő teljes visszaverődést létrehozva lineárisan poláros fényből cirkulárisan poláros fényt lehet előállítani. Ehhez még a p és s komponenseknek azonos amplitúdóval is kell rendelkezniük a 90º fáziskülönbség mellett. A szükséges fáziskülönbséget kétszeri teljes visszaverődés biztosítja, míg az amplitúdók egyenlőségéhez a beeső lineárisan poláros fény rezgési síkjának kell 45º szöget bezárnia a beesési síkkal. Ezen az elven működik az 5.6. ábrán vázolt Fresnel-féle hasáb. Ennek a párhuzamos lapjait úgy alakítják ki, hogy a leírt feltételek teljesüljenek. A hasáb be- és kilépő lapjára a fény merőlegesen esik, az oldalsó lapokon pedig belül teljes visszaverődés jön létre. A lapok szögét úgy választják meg, hogy a teljes visszaverődés okozta két komponens közötti fázistolás éppen 45º legyen. Ennek az értéke a hasáb anyagának törésmutatójától függ.

Az 5.28. egyenlet differenciálásával könnyen megkereshetjük tg(δ/2) maximumát. A maximum feltétele

,

(5.29)

amiből látható, hogy a maximumot biztosító beesési szögre

(5.30)

az összefüggés teljesül. Ezt visszahelyettesítve az 5.28. egyenletbe a maximum értékére a

(5.31)

egyenlet adódik. Ebből látható, hogy ahhoz, hogy a fázistolás elérje vagy meghaladja a 90º-ot

(5.32)

feltétel teljesülése szükséges. Ha az utóbbi feltételt a optikailag sűrűbb közegnek a ritkábbra vonatkozó törésmutatóval fejezzük ki, akkor a

(5.33)

relációt kapjuk, amely azt mutatja, hogy a törésmutatónak meglehetősen nagynak kell lennie. Bár léteznek ilyen törésmutatóval bíró nem-elnyelő anyagok, ilyen például a gyémánt, gyakorlatban mégis a 90º fázistolásnak két visszaverődésre történő elosztása terjedt el, hiszen ez üvegből készült hasábbal könnyen megvalósítható. Kiindulva a összefüggésből, az 5.31. egyenletből egyszerűen megmutatható, hogy ahhoz, hogy fázistolás elérje a 45º értéket a sűrűbb közegnek a ritkább közegre vonatkozó törésmutatójának teljesítenie kell az

(5.34)

feltételt. Az optikában használatos üvegek közül sok teljesíti ezt a feltételt. Az 5.5. ábrán látható esetre () az 5.30. és 5.31. egyenletek alapján a fáziskülönbség maximuma δ_m = 51.98º és ezt θ_b = 48.55º beesési szögnél éri el.

Az 5.10. és 5.11. egyenletek alapján az átmenő fény elektromos és mágneses térerősségét az

(5.35)

egyenletek adják, ahol a relatív törésmutató és a formula származtatásánál az valamint az 5.22. és az 5.7. összefüggéseket alkalmaztuk. Ebből látható, hogy az átmenő fény z irányba exponenciálisan csökkenő amplitúdójú, x irányba terjedő inhomogén síkhullámmal írható le. A hullám amplitúdója

(5.36)

távolságon csökken az e-ad részére, ahol λ_b a beeső hullám (közegbeli) hullámhossza. Ez a távolság arra jellemző, hogy milyen mélyen hatol be a hullám a ritkább közegbe.

Vizsgáljuk meg, hogy a törőfelületen (z = 0) milyen módon áramlik keresztül a fényenergia. Ehhez a Poynting-vektornak felületre merőleges

(5.37)

komponensét kell kiszámítanunk a határfelületen (z = 0), ahol az írott nagy betűk a valós térmennyiségeket jelölik, melyeket az eddigi komplex kifejezések valós része szolgáltat. Írjuk fel a T transzmissziós együtthatókat az

és

(5.38)

exponenciális alakba, ahol C_p és C_s nem-negatívak. Az 5.35. egyenletekből

(5.39)

egyenletek kapjuk a (valós) térerősségre, továbbá a (valós) mágneses térerősséget a

(5.40)

formulákból számíthatjuk ki. Az 5.39. és 5.40. összefüggéseket a z = 0 mellett az 5.37. egyenletbe helyettesítve és a azonosságot felhasználva a

(5.41)

formulát kapjuk a Poynting-vektor törőfelületre merőleges komponensére. Ebből látható, hogy az energia 2ω körfrekvenciával periodikusan áramlik oda-vissza a felületen keresztül. A térerősségek egy periódusa alatt kétszer be- és visszaáramlik az energia.  félperiódusra és ennek egész számú többszöröseire vonatkozó átlaga nulla. Ennek következtében a periódushoz képest sokkal hosszabb mérési időre vonatkozó átlagos energiaáram sűrűség a felületre merőleges irányba zérus (). Megmutatható, hogy a Poynting-vektor törőfelületbe eső komponensének az átlaga nem zérus, ezért a felület mentén még hosszabb megfigyelési időintervallumot tekintve az energia x irányba áramlik.