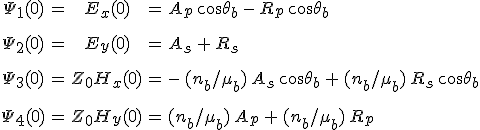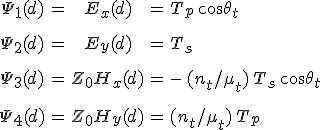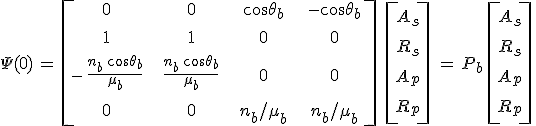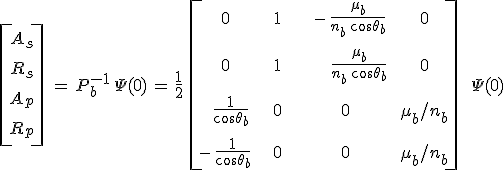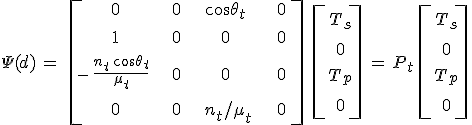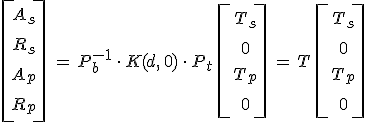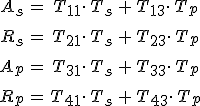Átviteli mátrix
Határfeltételek. Vetítési mátrixok
A 12.15. egyenletbeli Ψ vektort az elektromos és mágneses térerősségek x és y komponensei alkotják, ezért Ψ a határfelületeken folytonosan megy át. A feladat kitűzésénél alkalmazott jelöléseket használva az elektromos térerősségek amplitúdóira, a z = 0 síkban fennállnak a
|
|
(12.39) |
összefüggések. Az utolsó két kifejezésnél felhasználtuk az elektromos és mágneses térerősségek közötti kapcsolatot leíró 3.5. és a ![]() egyenleteket is. Teljesen hasonlóan a z = d síkban a térmennyiségek határfelületbeli folytonos átmenetét 12.39. kifejezésekkel analóg
egyenleteket is. Teljesen hasonlóan a z = d síkban a térmennyiségek határfelületbeli folytonos átmenetét 12.39. kifejezésekkel analóg
|
|
(12.40) |
egyenletek biztosítják, ahol a ![]() törési szöget az
törési szöget az ![]() összefüggés határozza meg. A 12.39. összefüggéseket a
összefüggés határozza meg. A 12.39. összefüggéseket a
|
|
(12.41a) |
vektori alakba írhatjuk, ahol a Pb mátrix az ún. bemeneti vetítési mátrix. A Jones-mátrixok kiszámolásához az inverz relációra lesz szükség. A Pb mátrix inverzét kiszámolva az
|
|
(12.41b) |
inverz összefüggést nyerjük. Hasonlóan a 12.40. egyenleteket is a
|
|
(12.42) |
vektori alakba alakíthatjuk át, ahol Pt az ún. kimeneti vetítési mátrix.
Átviteli mátrix
A 12.24. valamint a 12.41. és 12.42. egyenleteket felhasználva már könnyen meg tudjuk adni a beeső, a visszavert és az átengedett hullámok amplitúdói közötti viszonyt. A három egyenlet alapján
|
|
(12.43) |
kapcsolat áll fenn, ahol a
|
|
(12.44) |
mátrixot, - a bemeneti vetítési mátrix inverzének, a karakterisztikus mátrix és a kimeneti vetítési mátrix szorzatából előálló mátrixot - az anizotróp (rétegezett) közeg átviteli mátrixának nevezzük. A 12.43. egyenletben a jobb oldali vektorral való szorzást elvégezve, és a sorokat kiírva az
|
|
(12.45) |
egyenletekhez jutunk, ahol Tmj az átviteli mátrix elemeit jelölik (m, j = 1, 2, 3, 4).