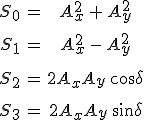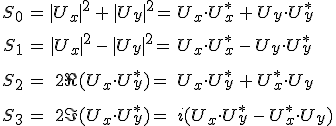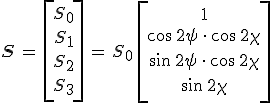Stokes-féle formalizmus

A 3.15. egyenletrendszerből a t időt kiküszöbölve (a Hullámtan és optika alapkurzusból is jól ismert)

egyenlethez jutunk, amely a 3.1. ábrán látható polarizációs ellipszis egyenlete. Az egyenletet a periódushoz képest sokkal hosszabb mérési időre átlagolva és  mennyiséggel beszorozva

összefüggést kapjuk. A monokromatikus fény energetikai viszonyait tárgyaló résznél látott módon a 3.15. egyenletekből az

,         és   

adódik az átlagokra. Ezeket visszahelyettesítve az

egyenlethez juthatunk, amelyhez a jól ismert    azonosságból egyből eljuthatunk. A baloldalon tagot hozzáadva és levonva, egyszerű átalakítással

(4.16)

formulát nyerjük. A 4.16. egyenletben megjelenő

(4.17)

mennyiségeket nevezzük monokromatikus síkhullám Stokes-féle paramétereinek. A 4.16. egyenletbe a paramétereket beírva és átrendezve látható, hogy a monokromatikus síkhullám Stokes-féle paraméterei között az

(4.18)

kapcsolat áll fen. Ha S₀ paramétert osztjuk 2Z-vel, akkor a hullám intenzitását kapjuk, vagyis az S₀ paraméter a hullám intenzitásával arányos mennyiség. Látható még, hogy a paraméterek azonos dimenzióval rendelkeznek, 2Z-vel osztva őket intenzitás dimenziójú fizikai mennyiséget kapunk. A paramétereknek egy állandóval való szorzása a polarizációs viszonyokon és az eddig felírt összefüggéseken nem változtatnak, így a 4.17. definíciók helyett a 2Z-vel osztott mennyiségek is használhatók Stokes-féle paraméterként. A Stokes-féle paraméterekből alkotott 4-dimenziós

(4.19)

oszlopvektort Stokes-féle vektornak szokás nevezni, ahol a T felső index a transzponálást jelöli. A paramétereknek vektorba való foglalása azért célszerű, mert az optikai elemen való áthaladás során a paraméterek sokszor lineáris módon változnak meg, így az optikai elemhez egy mátrix, az ún. Müller-féle mátrix rendelhető. A 4.1. táblázatban a 3. oszlopban látható néhány gyakorlatban is fontos S₀  (az intenzitásra) normált Stokes-féle vektor. Ezeket egyszerű számolással kaphatjuk meg a 4.17. egyenletek alapján.

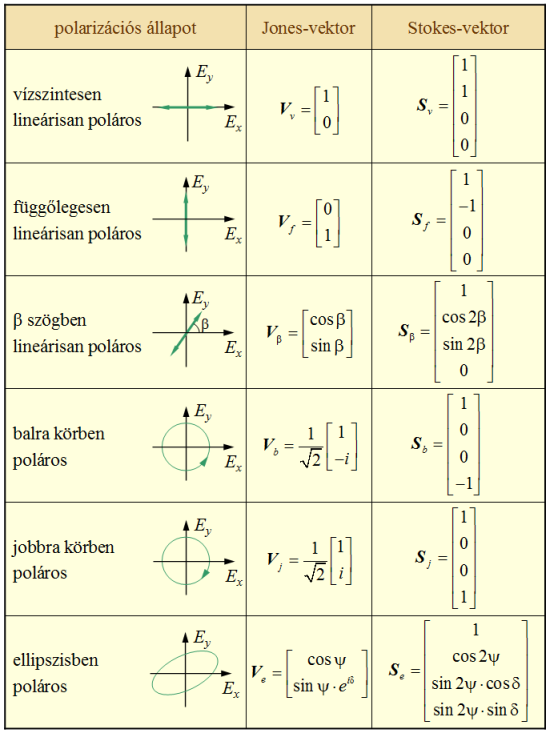4.1. táblázat. Példák normált Jones- és Stokes-féle vektorokra.

Mivel a számolásokat gyakran komplex írásmódban kényelmes elvégezni, így célszerű a Sokes-féle paramétereket is komplex írásmódban felírni. A 4.17. egyenletek egyszerűn átírhatók olyan alakban, amely a hullám komplex amplitúdóit tartalmazza, nevezetesen a paramétereket az

(4.20)

 formulákból számolhatjuk ki, ahol

  és  

a térerősség x és y komponenseinek a komplex amplitúdói (3.15. egyenlet).

A Stokes-paramétereket definiáló 4.17. egyenletekből valamint a 3.28. és a 3.31. összefüggésekből rögtön adódnak a

(4.21)

formulák. Ezeket a 4.18. egyenletbe helyettesítve egyszerű számolással kapjuk, hogy

.

(4.22)

A 4.21-22 egyenletekből látható, hogy a Stokes-féle vektort felírhatjuk az

(4.23)

alakba, azaz megadhatjuk a teljes intenzitással arányos S₀, a polarizációs ellipszis orientációját leíró ψ, valamint az ellipszis lapultságára jellemző χ segédszöget használva. A 4.23. előállítás alapján az (S₀, ψ, χ) rendezett hármast felfoghatjuk, mint egy (S₁, S₂, S₃) derékszögű koordinátákkal adott pont gömbi polárkoordinátáit, ahogy azt a 4.1. ábra szemlélteti. Így a polarizációs állapotokhoz egy S₀ sugarú gömbfelület pontjait rendelhetjük és megfordítva.  A gömb sugara az S₀ Stokes-féle paraméter, továbbá 2ψ az azimutszög és 2χ az egyenlítő síkjától mért polárszög. Látható, hogy az északi félteke pontja jobbra poláros (χ > 0), míg a déli félteke pontjai balra poláros (χ < 0) állapotokat írnak le. A pólusok cirkulárisan poláros, míg az egyenlítő pontjai lineárisan poláros állapotoknak felelnek meg. A polarizációs állapotok ezen geometriai szemléltetését Poincaré-féle gömbnek nevezzük.

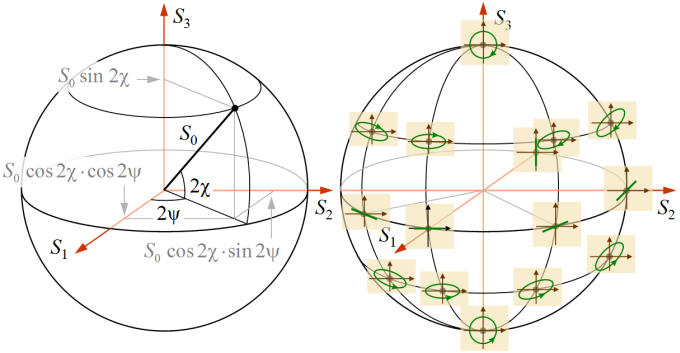4.1. ábra. A polarizációs állapotok szemléltetése a Poincaré-féle gömbön.