Csillapodó elektromágneses síkhullám
A hullám transzverzális természete
Láttuk, hogy az
| (7.17) |
kifejezések monokromatikus megoldásai a 7.2. illetve 7.3. egyenleteknek, és csillapodó síkhullámot írnak le (k0 = ω/c0). Az átlátszó közegekhez hasonlóan, azonban ahhoz, hogy ezek is kielégítsék a Maxwell-egyenleteket, még további, az amplitúdókra vonatkozó feltételek szükségesek.
A 7.3. egyenlet származtatásánál elmondottak miatt ![]() , ezért
, ezért
![]()
Amiből az következik hogy E0 és s merőlegesek ![]() . Hasonlóan a
. Hasonlóan a ![]() feltételből következik H0 és s merőlegessége
feltételből következik H0 és s merőlegessége ![]() . Az M-2 egyenletből és a 1.7. anyagegyenletből, azonos átalakításokkal
. Az M-2 egyenletből és a 1.7. anyagegyenletből, azonos átalakításokkal
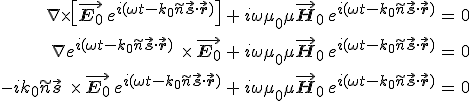
összefüggéseket kapjuk, amiből
| |
(7.18) |
egyenlethez jutunk, amely formailag azonos az átlátszó közegre kapott eredménnyel (3.5), csak a törésmutató komplex. Az M-1 egyenletet, az 1.3. anyagegyenletet és a differenciális Ohm-törvényt felhasználva, ekvivalens átlakításokkal
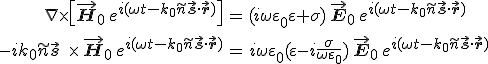
adódik, amiből
| (7.19) |
összefüggést kapjuk, amely az előbbihez hasonlóan formailag azonos az átlátszó közegben érvényes analóg összefüggéssel (3.7).
Az eredményünk meggyőzően mutatja a komplex írásmód sok előnyét. Komplex írásmódot használva, és bevezetve a komplex dielektromos állandót és a komplex törésmutatót eredményünk formailag megegyezik az átlátszó közegekre érvényes analóg formulákkal. A törésmutató komplex értéke miatt, a 7.18. vagy 7.19. formulákból következőleg, az átlátszó közegektől eltérően az elektromos és mágneses térerősségek között fáziskülönbség lép fel.
Érdemes még azt is megjegyezni, hogy az eddigi példákban s valós egységvektor volt, vagyis ténylegesen egy térbeli irányt adott meg. Azonban a 7.17-19 formulákkal leírt hullámok komplex s egységvektor (azaz ![]() ) esetén is a Maxwell-egyenletek megoldásai. Erre példát majd a következő alfejezetben látunk majd, mikor egy átlátszó és elnyelő közegeket szétválasztó határfelületen való törést és visszaverődést vizsgálunk.
) esetén is a Maxwell-egyenletek megoldásai. Erre példát majd a következő alfejezetben látunk majd, mikor egy átlátszó és elnyelő közegeket szétválasztó határfelületen való törést és visszaverődést vizsgálunk.