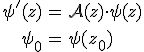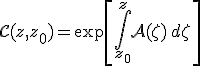Cauchy-féle mátrix
Alaprendszer és alapmátrix
A 6.18. vagy az azonos alakú 6.24. egyenletrendszer kétdimenziós speciális esete a
|
|
(6.26) |
vektori alakba írt elsőrendű differenciál-egyenletrendszernek, ahol ![]() az ismeretlen n-dimenziós vektorfüggvény és
az ismeretlen n-dimenziós vektorfüggvény és ![]()
![]() ismert mátrixfüggvény. Ismert, hogy egy ilyen egyenletnek bármely megoldása előállítható a
ismert mátrixfüggvény. Ismert, hogy egy ilyen egyenletnek bármely megoldása előállítható a ![]() (n darab) lineárisan független megoldásának lineáris kombinációjaként, azaz
(n darab) lineárisan független megoldásának lineáris kombinációjaként, azaz
|
|
(6.27) |
alakban. A 6.26. egyenlet n elemű lineárisan független megoldásainak rendszerét az egyenlet alaprendszerének nevezzük. A 6.27. előállítás szemléletesen azt jelenti, hogy az egyenlet megoldásai n dimenziós vektorteret alkotnak, és az alaprendszer ennek a vektortérnek egy bázisa, továbbá a ![]() állandók a vektor bázisra vonatkozó koordinátái. Ez alapján nyilvánvaló, hogy az alaprendszer nem egyértelmű, hiszen egy bázisról áttérhetünk egy másik bázisra, ahogy ez a szokásos vektoroknál is megtehető. A
állandók a vektor bázisra vonatkozó koordinátái. Ez alapján nyilvánvaló, hogy az alaprendszer nem egyértelmű, hiszen egy bázisról áttérhetünk egy másik bázisra, ahogy ez a szokásos vektoroknál is megtehető. A ![]() alaprendszer vektoraiból alkotott
alaprendszer vektoraiból alkotott
|
|
(6.28) |
mátrixot a 6.26. egyenlet alapmátrixának nevezzük. Mivel az alapmátrix oszlopvektorai megoldások, így maga az alapmátrix is kielégíti a 6.26. egyenletet, másrészt tetszőleges n-dimenziós ![]() vektor esetén
vektor esetén
|
|
(6.29) |
nyilván megoldás.
Az alapmátrix segítségével értelmezhetjük az
|
|
(6.30) |
ún. Cauchy-féle mátrixot, ahol az alapmátrix inverze biztosan létezik, hiszen F oszlopai lineárisan függetlenek. Mivel F alapmátrix (így oszlopai lineárisan függetlenek), rögzített z0 esetén M (már csak z függvénye) szintén alapmátrix. Könnyen belátható, hogy bár a Cauchy-mátrixot az alaprendszerrel definiáltuk, mégis független az alaprendszer megválasztásától. Másrészt z = z0 esetén nyilván az egység mátrixszal egyenlő, azaz
|
|
(6.31) |
A Cauchy-mátrix további fontos tulajdonsága, hogy tetszőleges z0, z1, z2 argumentumokra fennáll az
|
|
(6.32) |
reláció. Ezt speciálisan a z2 = z0 esetre alkalmazva és felhasználva a 6.31. tulajdonságot, adódik, hogy a Cauchy-mátrix inverzét a változóinak a felcserélésével kaphatjuk meg, azaz
|
|
(6.33) |
Az elmondottak alapján könnyen belátható, hogy a
|
|
(6.34) |
ún. kezdeti érték problémának a megoldása a Cauchy-mátrix ismeretében könnyen megadható a
|
|
(6.35) |
formában, ugyanis a Cauchy-mátrix maga is alapmátrix és így 6.29. egyenlet következtében 6.33. kifejezés a differenciálegyenlet megoldása, másrészt 6.31. tulajdonság miatt nyilván teljesül az előírt kezdeti feltétel is.
A Cauchy-mátrix meghatározása persze nem könnyű feladat, erre nincs általános módszer. Amennyiben az ![]() mátrix funkcionálisan felcserélhető, azaz
mátrix funkcionálisan felcserélhető, azaz
|
|
(6.36) |
reláció teljesül minden z és ζ értékre, akkor megmutatható, hogy
|
|
(6.37) |
az egyenlet Cauchy-mátrixa. Megmutatható, hogy egy 2×2-es ![]() mátrix akkor és csak akkor funkcionálisan felcserélhető, ha az
mátrix akkor és csak akkor funkcionálisan felcserélhető, ha az
|
|
(6.38) |
alakba írható, ahol a(z) és b(z) skalárfüggvények, és a1, a2, a3 állandók. Állandó vagyis z-től független ![]() mátrix - amely a funkcionálisan felcserélhetőség nyilvánvaló speciális esete -, 6.35. összefüggés alapján
mátrix - amely a funkcionálisan felcserélhetőség nyilvánvaló speciális esete -, 6.35. összefüggés alapján
|
|
(6.39) |
Érdemes megjegyezni, hogy a 6.39. egyenletben lévő mátrix exponenciális függvényt ritkán célszerű a definíciójául szolgáló
|
|
(6.40) |
hatványsora alapján kiszámolni. Ennek kiszámolására több módszer is ismeretes. Ezek közül egyet röviden ismertetünk. Lineáris algebrából ismert Cayley-Hamiton-tétel szerint bármely négyzetes mátrix gyöke a saját karakterisztikus egyenletének, azaz
|
|
(6.41) |
ahol ![]() karakterisztikus polinom, amely n×n-es mátrix esetén n-ed fokú polinom. A Cayley-Hamilton-tétel következtében az
karakterisztikus polinom, amely n×n-es mátrix esetén n-ed fokú polinom. A Cayley-Hamilton-tétel következtében az ![]() mátrix n-edik és ennél magasabb hatványai kifejezhetők az
mátrix n-edik és ennél magasabb hatványai kifejezhetők az ![]() mátrix (n-1)-ed fokú polinomjaként. Ezért a 6.40. hatványsor szintén kifejezhető az
mátrix (n-1)-ed fokú polinomjaként. Ezért a 6.40. hatványsor szintén kifejezhető az ![]() mátrix (n-1)-ed fokú polinomjaként, azaz
mátrix (n-1)-ed fokú polinomjaként, azaz
|
|
(6.42) |
ahol ![]() a polinom együtthatói. Az ismeretlen együtthatókat egy lineáris egyenletrendszer megoldásával kaphatjuk meg. Ha az
a polinom együtthatói. Az ismeretlen együtthatókat egy lineáris egyenletrendszer megoldásával kaphatjuk meg. Ha az ![]() mátrix p darab (p ≤ n) egymástól különböző sajátértékeit
mátrix p darab (p ≤ n) egymástól különböző sajátértékeit ![]() jelöli és ezek algebrai multiplicitásuk rendre
jelöli és ezek algebrai multiplicitásuk rendre ![]() , akkor megmutatható, hogy fennállnak az
, akkor megmutatható, hogy fennállnak az
|
|
(6.43) |
egyenletek, ahol ![]() és adott j esetén
és adott j esetén ![]() , valamint a felső (zárójeles) index a λ változó szerinti deriválást jelöli (a 0-adik deriválton magát a függvényt értjük). Látható, hogy a
, valamint a felső (zárójeles) index a λ változó szerinti deriválást jelöli (a 0-adik deriválton magát a függvényt értjük). Látható, hogy a ![]() sajátérték éppen az
sajátérték éppen az ![]() multiplicitásával azonos számú összefüggést szolgáltat, ezért az
multiplicitásával azonos számú összefüggést szolgáltat, ezért az ![]() miatt éppen n darab egyenletből álló lineáris egyenletrendszert kapunk az n darab ismeretlen rs együtthatóra. Az
miatt éppen n darab egyenletből álló lineáris egyenletrendszert kapunk az n darab ismeretlen rs együtthatóra. Az
|
|
(6.44) |
függvény szintén a 6.42. összefüggéssel adható meg, csak a kifejtés együtthatói a z változó függvényei lesznek, azaz
|
|
(6.45) |
Az ismeretlen együtthatókat a 6.43. lineáris egyenletrendszerből számíthatjuk ki, melyben z egy paraméterként jelenik meg. Az itt leírt módszerrel könnyen megmutatható, hogy például az
|
|
(6.46) |
Ugyancsak bizonyítás nélkül megemlítjük, hogy a 6.44. mátrix exponenciális függvény kiszámítható a Laplace-transzformáció segítségével is, ugyanis fennáll az
|
|
(6.47) |
összefüggés, ahol ![]() a Laplace-transzformáció inverzét, valamint z és p a transzformáció összetartozó változó párjait jelöli.
a Laplace-transzformáció inverzét, valamint z és p a transzformáció összetartozó változó párjait jelöli.